Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lachance, Michael A.
1984.
Rational Approximation and Interpolation.
Vol. 1105,
Issue. ,
p.
125.
Rahman, Qazi Ibadur
and
Schmeisser, Gerhard
1987.
Numerical Methods of Approximation Theory/Numerische Methoden der Approximationstheorie.
Vol. 81,
Issue. ,
p.
169.
Rahman, Q. I.
and
Schmeisser, G.
1988.
Markov-Duffin-Schaeffer inequality for polynomials with a circular majorant.
Transactions of the American Mathematical Society,
Vol. 310,
Issue. 2,
p.
693.
Pierre, R
Rahman, Q.I
and
Schmeisser, G
1989.
On polynomials with curved majorants.
Journal of Approximation Theory,
Vol. 57,
Issue. 2,
p.
211.
Rahman, Q.I
and
Watt, A.O
1992.
Polynomials with a parabolic majorant and the Duffin-Schaeffer inequality.
Journal of Approximation Theory,
Vol. 69,
Issue. 3,
p.
338.
Varma, A. K.
1993.
Markoff type inequalities for curved majorants in the weightedL 2 norm.
Aequationes mathematicae,
Vol. 45,
Issue. 1,
p.
24.
Burkett, J.
and
Varma, A. K.
1994.
Extremal properties of derivative of algebraic polynomials.
Acta Mathematica Hungarica,
Vol. 64,
Issue. 4,
p.
373.
Varma, A. K.
Mills, T. M.
and
Smith, Simon J.
1995.
Markoff type inequalities for curved majorants.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 58,
Issue. 1,
p.
1.
Guessab, A
and
Rahman, Q.I
1997.
Quadrature Formulae and Polynomial Inequalities.
Journal of Approximation Theory,
Vol. 90,
Issue. 2,
p.
255.
Nikolov, Geno
1998.
On Certain Duffin and Schaeffer Type Inequalities.
Journal of Approximation Theory,
Vol. 93,
Issue. 1,
p.
157.
Rack, Heinz-Joachim
2014.
Companion theorems to G. Szegö’s inequality for pairs of coefficients of bounded polynomials.
Periodica Mathematica Hungarica,
Vol. 68,
Issue. 1,
p.
54.
2022.
Extremal Problems and Inequalities of Markov-Bernstein Type for Algebraic Polynomial.
p.
391.
Gardner, Robert B.
Govil, Narendra K.
Milovanović, Gradimir V.
and
Rassias, Themistocles M.
2022.
Extremal Problems and Inequalities of Markov-Bernstein Type for Algebraic Polynomial.
p.
1.
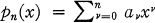 is a polynomial of degree at most n and |pn(x)| ≦ 1 in the interval –1 ≦ x ≦ 1, then in the same interval
is a polynomial of degree at most n and |pn(x)| ≦ 1 in the interval –1 ≦ x ≦ 1, then in the same interval