Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T01:28:09.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Cubature Formulae and Designs Obtained from Group Orbits

Published online by Cambridge University Press:  20 November 2018

Hiroshi Nozaki  and
Masanori Sawa
Hiroshi Nozaki
Affiliation:
Graduate School of Information Sciences, Tohoku University, Aoba-ku, Sendai 980-8579, Japan email: [email protected]
Masanori Sawa
Affiliation:
Graduate School of Information Sciences, Tohoku University, Aoba-ku, Sendai 980-8579, Japan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1960, Sobolev proved that for a finite reflection group 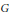$G$, a 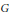$G$-invariant cubature formula is of degree 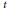$t$ if and only if it is exact for all 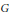$G$-invariant polynomials of degree at most 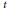$t$. In this paper, we make some observations on invariant cubature formulas and Euclidean designs in connection with the Sobolev theorem. First, we give an alternative proof of theorems by Xu (1998) on necessary and sufficient conditions for the existence of cubature formulas with some strong symmetry. The new proof is shorter and simpler compared to the original one by Xu, and, moreover, gives a general interpretation of the analytically-written conditions of Xu's theorems. Second, we extend a theorem by Neumaier and Seidel (1988) on Euclidean designs to invariant Euclidean designs, and thereby classify tight Euclidean designs obtained from unions of the orbits of the corner vectors. This result generalizes a theorem of Bajnok (2007), which classifies tight Euclidean designs invariant under the Weyl group of type 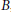$B$, to other finite reflection groups.

Keywords

65D3205E9951M99cubature formulaEuclidean designradially symmetric integralreflection groupSobolev theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1359 - 1377
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bajnok, B., On Euclidean designs. Adv. Geom. 6(2006), no. 3, 423–438. http://dx.doi.org/10.1515/ADVGEOM.2006.026 Google Scholar
[2] Bajnok, B., Orbits of the hyperoctahedral group as Euclidean designs. J. Algebraic Combin. 25(2007), no. 4, 375–397. http://dx.doi.org/10.1007/s10801-006-0042-3 Google Scholar
[3] Bannai, Ei. and Bannai, Et., On Euclidean tight 4-designs. J. Math. Soc. Japan 58(2006), no. 3, 775–804. http://dx.doi.org/10.2969/jmsj/1156342038 Google Scholar
[4] Bannai, Ei. and Bannai, Et., A survey on spherical designs and algebraic combinatorics on spheres. European J. Combin. 30(2009), no. 6, 1392–1425. http://dx.doi.org/10.1016/j.ejc.2008.11.007 Google Scholar
[5] Bannai, Ei., Bannai, Et., Hirao, M., and Sawa, M., Cubature formulas in numerical analysis and Euclidean tight designs. European J. Combin. 31(2010), no. 2, 423–441. http://dx.doi.org/10.1016/j.ejc.2009.03.035 Google Scholar
[6] Bannai, Et., New examples of Euclidean tight 4-designs. European J. Combin. 30(2009), no. 3, 655–667. http://dx.doi.org/10.1016/j.ejc.2008.07.012 Google Scholar
[7] Bannai, Et., On antipodal Euclidean tight (2e + 1)-designs. J. Algebraic Combin. 24(2006), no. 4, 391–414. http://dx.doi.org/10.1007/s10801-006-0007-6 Google Scholar
[8] Bourbaki, N., Lie groups and Lie algebras: Chapters 4-6 In: Elements of Mathematics, Springer-Verlag, Berlin, 2002.Google Scholar
[9] Delsarte, P., Goethals, J. M., and Seidel, J. J., Spherical codes and designs. Geometriae Dedicata 6(1977), no. 3, 363–388. http://dx.doi.org/10.1007/BF03187604 Google Scholar
[10] Delsarte, P. and Seidel, J. J., Fisher type inequalities for Euclidean t-designs. Linear Algebra Appl. 114/115(1989), 213–230. http://dx.doi.org/10.1016/0024-3795(89)90462-X Google Scholar
[11] Dunkl, C. F. and Xu, Y., Orthogonal polynomials of several variables. Encyclopedia of Mathematics and its Applications, 81, Cambridge University Press, Cambridge, 2001.Google Scholar
[12] Erdělyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F., Higher transcendental functions. II. (Bateman Manuscript Project), Mac Graw-Hill, New York-Toronto-London, 1953.Google Scholar
[13] Goethals, J. M. and Seidel, J. J., Cubature formulae, polytopes, and spherical designs. In: The geometric vein, Springer, New York-Berlin, 1981, pp. 203–218.Google Scholar
[14] Hirao, M. and Sawa, M., On minimal cubature formulae of small degree for spherically symmetric integrals. SIAM J. Numer. Anal. 47(2009), no. 9, 3195–3211. http://dx.doi.org/10.1137/070711207 Google Scholar
[15] Li, H. and Xu, Y., Discrete Fourier analysis on fundamental domain of Ad-lattice and on simplex in d-variables. J. Fourier Anal. Appl. 16(2010), no. 3, 383–433. http://dx.doi.org/10.1007/s00041-009-9106-9 Google Scholar
[16] Möller, H. M., Lower bounds for the number of nodes in cubature formulae. In: Numerische integration (Tagung, Math. Forschungsinst., Oberwolfach, 1978), Internat. Ser. Numer. Math., 45, Birkhäuser, Basel-Boston, Mass., 1979, pp. 221-230.Google Scholar
[17] Moody, R. V. and Patera, J., Cubature formulae for orthogonal polynomials in terms of elements of finite order of compact simple Lie groups. Adv. in Appl. Math. 47(2011), no. 3, 509–539. http://dx.doi.org/10.1016/j.aam.2010.11.005 Google Scholar
[18] Mysovskikh, I. P., Construction of cubature formulae. (Russian) Vopr. Vychisl. i Prikl. Mat. Tashkent 32(1975), 85–98.Google Scholar
[19] Mysovskikh, I. P., Interpolatory Type Cubature formula. (Russian) Nauka, Moscow, 1981.Google Scholar
[20] Neumaier, A. and Seidel, J. J., Discrete measures for spherical designs, eutactic stars and lattices. Nederl. Akad.Wetensch. Indag. Math. 50(1988), no. 3, 321–334.Google Scholar
[21] Nozaki, H., On the rigidity of spherical t-designs that are orbits of reflection groups E8 and H4. European J. Combin. 29(2008), no. 7, 1696–1703. http://dx.doi.org/10.1016/j.ejc.2007.09.003 Google Scholar
[22] Sali, A., On the rigidity of spherical t-designs that are orbits of finite reflection groups. Des. Codes Cryptogr. 4(1994), no. 2, 157–170. http://dx.doi.org/10.1007/BF01578869 Google Scholar
[23] Salikhov, G. N., Cubature formulas for the hypersphere invariant with respect to the group of the regular 600-gon. (Russian) Dokl. Akad. Nauk SSSR 223(1975), no. 5, 1075–1078.Google Scholar
[24] Sobolev, S. L., Cubature formulas on the sphere which are invariant under transformations of finite rotation groups. (Russian) Dokl. Akad. Nauk SSSR 146(1962), 310–313.Google Scholar
[25] Stroud, A. H., Approximate calculation of multiple integrals. Prentice-Hall Series in Automatic Computation, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1971.Google Scholar
[26] Verlinden, P. and Cools, R., On cubature formulae of degree 4k + 1 attaining Möller's lower bound for integrals with circular symmetry. Numer. Math. 61(1992), no. 3, 395–407. http://dx.doi.org/10.1007/BF01385517 Google Scholar
[27] Xu, Y., Minimal cubature formulae for a family of radial weight functions. Adv. Comput. Math. 8(1998), no. 4, 367–380. http://dx.doi.org/10.1023/A:1018964818105Google Scholar