Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:35:35.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Norm Convergence in Ergodic Theory and the Behavior of Fourier Transforms

Published online by Cambridge University Press:  20 November 2018

Joseph Rosenblatt
Joseph Rosenblatt*
Affiliation:
Mathematics Department Ohio State University Columbus, Ohio 43210 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Lp-norm convergence of weighted averages μnf is ergodic theory is equivalent to the pointwise convergence of the Fourier transforms 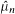. If h(γ) = 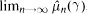, then the behavior of h determines when the Lp-norm limit of μnf is ∫f dm. The nature of such limit functions h is the focus of this article.

Keywords

2843
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 1 , 01 February 1994 , pp. 184 - 199
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Bellow, A., Jones, R. and Rosenblatt, J., Almost everywhere convergence of weighted averages, Math. Ann. 293(1992), 399–426.Google Scholar
2. Blum, J. R. and Hanson, D. L., On the mean ergodic theorem for subsequences, Bull. Amer. Math. Soc. 66(1960)308-311.Google Scholar
3. Boshernitzan, M., Slow uniform distribution, preprint.Google Scholar
4. Cornfeld, I. P., Fornin, S. V. and Ya G. Sinai, Ergodic Theory, Springer-Verlag, New York, 1972.Google Scholar
5. Feller, W., An Introduction to Probabilty Theory and its Applications, Vol. II, John Wiley and Sons, New York, 1971.Google Scholar
6. Jones, R., J. Rosenblatt and A. Tempel'man, Ergodic theorems for group actions, Illinois J. Math, to appear.Google Scholar
7. Kahane, J-P, Some Random Series of Functions, 2nd. Edition, Cambridge University Press, Cambridge, 1985.Google Scholar
8. Kuipers, L. and H. Niederreiter, Uniform Distribution of Sequences, Wiley, New York, 1974.Google Scholar
9. Lindahl, L-A. and F. Poulsen, Thin Sets in Harmonic Analysis, Marcel Dekker, New York, 1971.Google Scholar
10. Parry, W., Topics in Ergodic Theory, Cambridge University Press, Cambridge, 1981.Google Scholar
11. Petersen, K., Ergodic Theory, Cambridge University Press, Cambridge, 1983.Google Scholar
12. Rosenblatt, J., Universally bad sequences in ergodic theory, Almost Everywhere Convergence, II, Proceedings of the Conference on A.E. Convergence and Probability Theory, Fall, 1989, Northwestern University, Academic Press, New York, 1991, 227–246.Google Scholar
13. Schmidt, K., Asymptotic properties of unitary representations and mixing, Proc. London Math. Soc. (3) 48(1984)445-460.Google Scholar
14. Walters, P., An Introduction to Ergodic Theory, Springer-Verlag, New York-Heidelberg-Berlin, 1982.Google Scholar