No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
The Banach convolution algebras 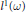 ${{l}^{1}}(\omega )$ and their continuous counterparts
${{l}^{1}}(\omega )$ and their continuous counterparts 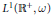 ${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ are much studied, because (when the submultiplicative weight function
${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ are much studied, because (when the submultiplicative weight function 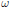 $\omega $ is radical) they are pretty much the prototypic examples of commutative radical Banach algebras. In cases of “nice” weights
$\omega $ is radical) they are pretty much the prototypic examples of commutative radical Banach algebras. In cases of “nice” weights 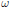 $\omega $, the only closed ideals they have are the obvious, or “standard”, ideals. But in the general case, a brilliant but very difficult paper of Marc Thomas shows that nonstandard ideals exist in
$\omega $, the only closed ideals they have are the obvious, or “standard”, ideals. But in the general case, a brilliant but very difficult paper of Marc Thomas shows that nonstandard ideals exist in 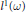 ${{l}^{1}}(\omega )$. His proof was successfully exported to the continuous case
${{l}^{1}}(\omega )$. His proof was successfully exported to the continuous case 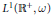 ${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ by Dales and McClure, but remained difficult. In this paper we first present a small improvement: a new and easier proof of the existence of nonstandard ideals in
${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ by Dales and McClure, but remained difficult. In this paper we first present a small improvement: a new and easier proof of the existence of nonstandard ideals in 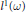 ${{l}^{1}}(\omega )$ and
${{l}^{1}}(\omega )$ and 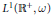 ${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$. The new proof is based on the idea of a “nonstandard dual pair” which we introduce. We are then able to make a much larger improvement: we find nonstandard ideals in
${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$. The new proof is based on the idea of a “nonstandard dual pair” which we introduce. We are then able to make a much larger improvement: we find nonstandard ideals in 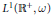 ${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ containing functions whose supports extend all the way down to zero in
${{L}^{1}}\left( {{\mathbb{R}}^{+}},\omega \right)$ containing functions whose supports extend all the way down to zero in 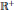 ${{\mathbb{R}}^{+}}$, thereby solving what has become a notorious problem in the area.
${{\mathbb{R}}^{+}}$, thereby solving what has become a notorious problem in the area.