Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:54:37.687Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Proof of the Hansen—Mullen Irreducibility Conjecture

Published online by Cambridge University Press:  20 November 2018

Aleksandr Tuxanidy  and
Qiang Wang
Aleksandr Tuxanidy
Affiliation:
School of Mathematics and Statistics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario K1S 5B6, e-mail: [email protected] , [email protected]
Qiang Wang
Affiliation:
School of Mathematics and Statistics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario K1S 5B6, e-mail: [email protected] , [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a new proof of the Hansen–Mullen irreducibility conjecture. The proof relies on an application of a (seemingly new) sufficient condition for the existence of elements of degree $n$ in the support of functions on finite fields. This connection to irreducible polynomials is made via the least period of the discrete Fourier transform 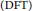$\left( \text{DFT} \right)$ of functions with values in finite fields. We exploit this relation and prove, in an elementary fashion, that a relevant function related to the 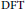$\text{DFT}$ of characteristic elementary symmetric functions (that produce the coefficients of characteristic polynomials) satisfies a simple requirement on the least period. This bears a sharp contrast to previous techniques employed in the literature to tackle the existence of irreducible polynomials with prescribed coefficients.

Keywords

11T06irreducible polynomialprimitive polynomialHansen–Mullen conjecturesymmetric functionq-symmetricdiscrete Fourier transformfinite field
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1373 - 1389
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Aigner, M. and Ziegler, G. M., Proofs from the book. 4th éd., Springer-Verlag, Berlin, 2010.Google Scholar
[2] Barvinok, A., Matrices with prescribed row and column sums. Linear Algebra Appl. 436 (2012), no. 4, 820–844. http://dx.doi.Org/10.1016/j.laa.2O10.11.019Google Scholar
[3] Bourgain, J., Prescribing the binary digits of primes, II. Israel J. Math. 206 (2015), no. 1, 165-182. http://dx.doi.org/10.1007/s11856-014-1129-5Google Scholar
[4] Canteaut, A. and Videau, M., Symmetric boolean functions. IEEE Transactions on Information Theory, Institute of Electrical and Electronics Engineers 51 (2005), no. 8, 2791–2811. http://dx.doi.org/10.1109/TIT.2005.851743Google Scholar
[5] Carlitz, L., A theorem of Dickson on irreducible polynomials. Proc. Amer. Math. Soc. 3 (1952), 693–700. http://dx.doi.org/10.1090/S0002-9939-1952-0049940-6Google Scholar
[6] Castro, F. N. and Medina, L. A., Linear recurrences and asymptotic behaviour of exponential sums of symmetric boolean functions. Electr. J. Comb. 18 (2011), no. 2, paper #P9.Google Scholar
[7] Cohen, S. D., Primitive polynomials over small fields. In: Finite fields and applications. Lecture Notes in Comput. Sci., 2948. Springer, Berlin, 2004, pp. 197–214.Google Scholar
[8] Cohen, S. D., Primitive polynomials with a prescribed coefficient. Finite Fields Appl. 12 (2006), no. 3, 425–491. http://dx.doi.Org/10.1016/j.ffa.2005.08.001Google Scholar
[9] Cohen, S. D. and Presern, M., Primitive polynomials with prescribed second coefficient. Glasgow Math. J. 48 (2006), 281–307. http://dx.doi.org/10.1017/S0017089506003077Google Scholar
[10] Cohen, S. D. and Presern, M., The Hansen-Mullen primitivity conjecture: completion of proof. In: Number theory and polynomials. London Math. Soc. Lecture Note Ser., 352. Cambridge University Press, Cambridge, 2008, pp. 89–120.Google Scholar
[11] Dorsey, T. and Hales, A. W., Irreducible coefficient relations. Sequences and their applications-SETA. 2012, Lecture Notes in Comput. Sci., 7280. Springer, Heidelberg, 2012 , pp. 117–125.Google Scholar
[12] Fan, S. Q. and Han, W. B., p-Adic formal series and primitive polynomials over finite fields. Proc. Amer. Math. Soc. 132 (2004), 15–31. http://dx.doi.org/10.1090/S0002-9939-03-07040-0Google Scholar
[13] Fitzgerald, R. W. and Yucas, J. L., Irreducible polynomials over GF(2) with three prescribed coefficients. Finite Fields Appl. 9 (2003), 286–299. http://dx.doi.Org/10.1016/S1071-5797(03)00005-4Google Scholar
[14] Garefalakis, T., Irreducible polynomials with consecutive zero coefficients. Finite Fields Appl. 14 (2008), no. 1, 201–208. http://dx.doi.Org/10.1016/j.ffa.2006.11.002Google Scholar
[15] Ha, J., Irreducible polynomials with several prescribed coefficients. Finite Fields Appl. 40 (2016), 10–25. http://dx.doi.0rg/IO.IOI6/j.ffa.2016.O2.OO6Google Scholar
[16] Ham, K. H. and Mullen, G. L., Distribution of irreducible polynomials of small degrees over finite fields.Math. Comp. 67 (1998), no. 221, 337–341. http://dx.doi.org/10.1090/S0025-5718-98-00904-1Google Scholar
[17] Han, W. B., On Cohen's problem. Chinacrypt ‘96, Academic Press (China) (1996) 231-235 (Chinese).Google Scholar
[18] Hansen, T. and Mullen, G. L., Primitive polynomials over finite fields. Math. Comp. 59 (1992), 639–643. http://dx.doi.org/10.1090/S0025-5718-1992-1134730-7Google Scholar
[19] Koç, Ç. K., Open problems in mathematics and computational science. Springer International Publishing, 2014.Google Scholar
[20] Kononen, K., Moisio, M., Rinta-aho, M., and Vâânânen, K., Irreducible polynomials with prescribed trace and restricted norm. JP J. Algebra Number Theory Appl. 11 (2009), 223–248.Google Scholar
[21] van Lint, J. H. and Wilson, R. M., A course in combinatorics. 2nd éd., Cambridge University Press, Cambridge, 2001.Google Scholar
[22] Koma, B. Omidi, Panario, D., and Wang, Q., The number of irreducible polynomials of degree n over ¥q with given trace and constant terms. Discrete Math. 310 (2010), 1282–1292. http://dx.doi.Org/10.1016/j.disc.2009.12.006Google Scholar
[23] Panario, D. and Tzanakis, G., A generalization of the Hansen-Mullen conjecture on irreducible polynomials over finite fields. Finite Fields Appl. 18 (2012), no. 2, 303–315. http://dx.doi.Org/10.1016/j.ffa.2O11.09.003Google Scholar
[24] Tuxanidy, A. and Wang, Q., On the number of N -free elements with prescribed trace. J. Number Theory 160 (2016), 536–565. http://dx.doi.Org/10.1016/j.jnt.2015.09.008Google Scholar
[25] Pollack, P., Irreducible polynomials with several prescribed coefficients. Finite Fields Appl. 22 (2013), 70–78. http://dx.doi.Org/10.1016/j.ffa.2013.03.001Google Scholar
[26] Ren, D.-B., On the coefficients of primitive polynomials over finite fields. Sichuan Daxue Xuebao 38 (2001), 33–36.Google Scholar
[27] Shparlinski, I. E., On primitive polynomials. Prob. Peredachi Inform. 23 (1988), 100–103 (Russian).Google Scholar
[28] Tzanakis, G., On the existence of irreducible polynomials with prescribed coefficients over finite fields. Master's thesis, Carleton University, 2010. //www.math.carleton.ca/∼gtzanaki/mscthesis.pdfGoogle Scholar
[29] Wan, D., Generators and irreducible polynomials over finite fields. Math. Comp. 66 (1997), no. 219, 1195–1212. http://dx.doi.org/10.1090/S0025-5718-97-00835-1Google Scholar