Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T14:42:18.820Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Group Algebra for Locally Compact Groups II

Published online by Cambridge University Press:  20 November 2018

John Ernest
John Ernest*
Affiliation:
University of Rochester Rochester, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In an earlier work, we defined and described a new group algebra 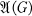, which is a von Neumann algebra containing the group G (3). In this paper we continue this study be relating the lattice of normal subgroups of the group G to the lattice of central projections of the group algebra 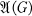. More precisely, we shall exhibit a one-to-one mapping ϕ of the lattice of closed normal subgroups of G into the lattice of central projections of 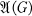, having the property that if N1 ⊂ N2, then ϕ(N2) ≤ ϕ(N1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 604 - 615
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Dixmier, J., Les algèbres d'opérateurs dans l'espace Hilbertien (algèbres de von Neumann) (Paris, 1957).Google Scholar
2. Ernest, J., A decomposition theory for unitary representations of locally compact groups, Trans. Amer. Math. Soc, 104 (1962), 252–277.Google Scholar
3. Ernest, J., Anew group algebra for locally compact groups, Amer. J. Math., 86 (1964), 467–492.Google Scholar
4. Ernest, J., Notes on the duality theorem of non-commutative non-compact topological groups, Töhoku Math. J., 15 (1963), 182–186.Google Scholar
5. G. Fell, J. M., C*-algebras with smooth dual, Illinois J. Math. 4 (1960), 221–230.Google Scholar
6. Kaplansky, I., Some aspects of analysis and probability, Surveys in Appl. Math. IV.Google Scholar
7. Mackey, G. W., Induced representations and normal subgroups, Proc. Internat. Symp. Linear Spaces (Jerusalem) (Oxford, 1961), pp. 319–326.Google Scholar
8. Mackey, G. W., Induced representations of locally compact groupsll. The Frobenius reciprocity theorem, Ann. of Math. 58 (1953), 193–221.Google Scholar
9. Naimark, M. A., Normed rings (Groningen, 1959).Google Scholar