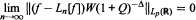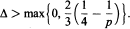Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Damelin, S.B.
1998.
The Lebesgue Function and Lebesgue Constant of Lagrange Interpolation for Erdoős Weights.
Journal of Approximation Theory,
Vol. 94,
Issue. 2,
p.
235.
Lubinsky, D. S.
1998.
Recent Progress in Inequalities.
p.
213.
Damelin, S. B.
and
Diethelm, Kai
2001.
BOUNDEDNESS AND UNIFORM NUMERICAL APPROXIMATION OF THE WEIGHTED HILBERT TRANSFORM ON THE REAL LINE.
Numerical Functional Analysis and Optimization,
Vol. 22,
Issue. 1-2,
p.
13.
Damelin, S.B.
Jung, H.S.
and
Kwon, K.H.
2001.
On mean convergence of Hermite–Fejér and Hermite interpolation for Erdős weights.
Journal of Computational and Applied Mathematics,
Vol. 137,
Issue. 1,
p.
71.
Damelin, S.B.
Jung, H.S.
and
Kwon, K.H.
2001.
A note on mean convergence of Lagrange interpolation in L(0<p⩽1).
Journal of Computational and Applied Mathematics,
Vol. 133,
Issue. 1-2,
p.
277.
Damelin, S.B.
Jung, H.S.
and
Kwon, K.H.
2001.
Necessary conditions for weighted mean convergence of Lagrange interpolation for exponential weights.
Journal of Computational and Applied Mathematics,
Vol. 132,
Issue. 2,
p.
357.
Damelin, S.B.
Jung, H.S.
and
Kwon, K.H.
2001.
Convergence of Hermite and Hermite–Fejér Interpolation of Higher Order for Freud Weights.
Journal of Approximation Theory,
Vol. 113,
Issue. 1,
p.
21.
Damelin, S.B.
2003.
Marcinkiewicz–Zygmund inequalities and the numerical approximation of singular integrals for exponential weights: methods, results and open problems, some new, some old.
Journal of Complexity,
Vol. 19,
Issue. 3,
p.
406.
Jung, H.S.
2003.
L∞ convergence of interpolation and associated product integration for exponential weights.
Journal of Approximation Theory,
Vol. 120,
Issue. 2,
p.
217.
Jung, H.S.
2005.
Necessary conditions of convergence of Hermite–Fejér interpolation polynomials for exponential weights.
Journal of Approximation Theory,
Vol. 136,
Issue. 1,
p.
26.
Pan, Yi Ge
2007.
Christoffel functions and mean convergence for Lagrange interpolation for exponential weights.
Journal of Approximation Theory,
Vol. 147,
Issue. 2,
p.
169.
Jung, Hee Sun
and
Sakai, Ryozi
2012.
Mean and uniform convergence of Lagrange interpolation with the Erdős-type weights.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Lubinsky, D. S.
2020.
Trigonometric Sums and Their Applications.
p.
119.
2024.
Near Extensions and Alignment of Data in ℝ n.
p.
149.
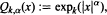
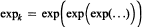 is the k-th iterated exponential. Following is our main result: Let 1 < p < ∞, Δ ∊ ℝ, k > 0. Let Ln[f] denote the Lagrange interpolation polynomial to ƒ at the zeros of pn(W2, x) = pn(e-2Q, x). Then for
is the k-th iterated exponential. Following is our main result: Let 1 < p < ∞, Δ ∊ ℝ, k > 0. Let Ln[f] denote the Lagrange interpolation polynomial to ƒ at the zeros of pn(W2, x) = pn(e-2Q, x). Then for