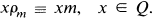Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:54:12.008Z Has data issue: false hasContentIssue false
  • English
  • Français

The Multiplicative Groups of Quasifields

Published online by Cambridge University Press:  20 November 2018

Michael J. Kallaher
Michael J. Kallaher*
Affiliation:
Washington State University, Pullman, Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (Q, +, ·) be a finite quasifield of dimension d over its kernel K = GF(q), where q = pk with p a prime and k ≧ 1. (See p. 18-22 and p. 74 of [7] or Section 5 of [9] for the definition of quasifield.) For the remainder of this article we will follow standard conventions and omit, whenever possible, the binary operations + and · in discussing a quasifield. For example, the notation Q will be used in place of the triple (Q, +, ·) and Q* will be used to represent the multiplicative loop (Q − {0}, ·).

Let m be a non-zero element of the quasifield Q; the right multiplicative mapping ρm:Q → Q is defined by

1

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 4 , 01 August 1987 , pp. 784 - 793
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Albert, A. A., On the collineation groups of certain non-desarguesian planes, Portugal. Math. 75 (1959), 207–224.Google Scholar
2. Bruck, R. H. and Bose, R. C., Linear representations of projective planes in projective spaces, J. Algebra 4 (1966), 117–172.Google Scholar
3. Dembowski, P., Finite geometries (Springer-Verlag, Berlin-Heidelberg-New York, 1968).CrossRefGoogle Scholar
4. Foulser, D. A., A generalization of Andre's systems, Math. Z. 100 (1967), 380–395.Google Scholar
5. Hering, C., Zweifach transitive Permutationsgruppen in denen 2 die maximale Anzahl von Fixpunkten von Involutionen ist, Math. Z. 104 (1968), 150–174.Google Scholar
6. Huppert, B., Zweifach transitive auflôsbare Permutationsgruppen, Math. Z. 68 (1957), 126–150.Google Scholar
7. Kallaher, M. J., Affine planes with transitive collineation groups, (North Holland, New York-Amsterdam-Oxford, 1982).Google Scholar
8. Kallaher, M. J. and Ostrom, T. G., Fixed point free linear groups, rank three planes, and Bol quasifields, J. Algebra 18 (1971), 159–178.Google Scholar
9. Lüneburg, H., Translation planes (Springer-Verlag, Berlin-Heidelberg-New York, 1980).CrossRefGoogle Scholar
10. Ostrom, T. G., A characterization of generalized André planes, Math. Z. 110 (1969), 1–9.Google Scholar
11. Passman, D. S., Permutation groups, (Benjamin, New York-Amsterdam, 1968).Google Scholar
12. Rao, M. L. N., Characterization of Foulser's λ-systems, Proc. Amer. Math. Soc. 24 (1970), 538–544.Google Scholar