Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T16:26:28.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Moore Cohomology and Central Twisted Crossed Product C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Judith A. Packer
Judith A. Packer*
Affiliation:
Department of Mathematics, National University of Singapore, Kent Ridge, Singapore 0511
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact second countable group, let X be a locally compact second countable Hausdorff space, and view C(X, T) as a trivial G-module. For G countable discrete abelian, we construct an isomorphism between the Moore cohomology group Hn(G, C(X, T)) and the direct sum Ext(Hn-1(G), Ȟl(βX, Ζ)) ⊕ C(X, Hn(G, T)); here Ȟ1 (βX, Ζ) denotes the first Čech cohomology group of the Stone-Čech compactification of X, βX, with integer coefficients. For more general locally compact second countable groups G, we discuss the relationship between the Moore group H2(G, C(X, T)), the set of exterior equivalence classes of element-wise inner actions of G on the stable continuous trace C*-algebra C0(X) ⊗ 𝒦, and the equivariant Brauer group BrG(X) of Crocker, Kumjian, Raeburn, and Williams. For countable discrete abelian G acting trivially on X, we construct an isomorphism 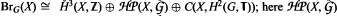is the group of equivalence classes of principal Ĝ bundles over X first considered by Raeburn and Williams.

Keywords

46L0546L3555N9155R10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 1 , 01 February 1996 , pp. 159 - 174
Copyright
Copyright © Canadian Mathematical Society 1997

References

[BP] Baggett, L. and Packer, J., The primitive ideal space of two-step nilpotent group C* -algebras, J. Funct. Anal, 124(1994), 389–426.Google Scholar
[Br] Brown, K., Cohomology of Groups. Springer-Verlag, New York, 1982.Google Scholar
[CKRW] Crocker, D., Kumjian, A., Raeburn, I. and Williams, D., An equivariant Brauer group and actions of groups on C*-algebras, submitted.Google Scholar
[ER] Echterhoff, S. and Rosenberg, J., Fine structure of the Mackey machine for actions of abelian groups with constant Mackey obstruction, Pacific J. Math., to appear.Google Scholar
[E] Elliott, G., Ideal-preserving automorphisms ofpostliminary C* -algebras, Proc. Amer. Math. Soc. 27(1971), 107–109.Google Scholar
[G] Grothendieck, A., Sur quelquespoints d'algèbre homologique, Tôhoku Math. J. 9(1957), 119–221.Google Scholar
[HR] Herman, R. and Rosenberg, J., Norm-close group actions on C*-algebras, J. Operator Theory 6(1981), 25–37.Google Scholar
[HORR] Hurder, S., Olesen, D., Raeburn, I. and Rosenberg, J., The Connes spectrum for actions of abelian groups on continuous trace C*-algebras, Ergodic Theory Dynamical Systems 6(1986), 541–560.Google Scholar
[L] Lance, E.C., Automorphisms of certain operator algebras, Amer. J. Math. 91(1969), 785–806.Google Scholar
[Ml] Moore, C., Extensions and low dimensional cohomology theory of locally compact groups, II, Trans. Amer. Math. Soc. 113(1964), 64–86.Google Scholar
[M2] Moore, C., Group extensions and cohomology for locally compact groups, III, Trans. Amer. Math. Soc. 221(1976), 35–58.Google Scholar
[OR] Olesen, D. and Raeburn, I., Pointwise unitary automorphism groups, J. Funct. Anal. 93(1990), 278–309.Google Scholar
[PR] Packer, J. and Raeburn, I., Twisted crossed products of C*-algebras, Math. Proc. Cambridge Philos. Soc. 106(1989), 293–311.Google Scholar
[P] Palais, R., On the existence of slices for actions of non-compact Lie groups, Ann. of Math. 73(1961), 295–323.Google Scholar
[PhR1] Phillips, J. and Raeburn, I., Automorphisms of C-algebras and second Cech cohomology, Indiana Univ. Math. J. 29(1990), 799–822.Google Scholar
[PhR2] Phillips, J., Crossed products by locally unitary automorphism groups and principal bundles, J. Operator Theory 11(1984), 215–241.Google Scholar
[RR] Raeburn, I. and Rosenberg, J., Crossed products of continuous trace C*-algebras by smooth actions, Trans. Amer. Math. Soc. 305(1988), 1–45.Google Scholar
[RW1] Raeburn, I. and Williams, D., Moore cohomology, principal bundles, and actions of groups on C*- algebras, Indiana Univ. Math. J. 40(1991), 707–740.Google Scholar
[RW2] Raeburn, I. and Williams, D., Dixmier-Douady classes of dynamical systems and crossed products, Canad. J. Math., 45 (1993. 1032–1066.Google Scholar
[Ro] Rosenberg, J., Some results on cohomology with Borel cochains, with applications to groups actions on operator algebras. In: Advances on Invariant Subspaces and Other Results, Operator Theory, Adv. Appl. 17, Birkhauser, Basel, Boston, 1986. 301–330.Google Scholar
[Sm1] Smith, H., Commutative twisted group algebras, Trans. Amer. Math. Soc. 197(1974), 315–326.Google Scholar
[Sm2] Smith, H., Characteristic principal bundles, Trans. Amer. Math. Soc. 211(1975), 365–375.Google Scholar
[Sm3] Smith, H., Central twisted group algebras, Trans. Amer. Math. Soc. 238(1978), 309–320.Google Scholar
[V] Vick, J., Homology Theory. Academic Press, New York, San Francisco, London, 1973.Google Scholar
[P] Palais, R., On the existence of slices for actions of non-compact Lie groups, Ann. of Math. 73(1961), 295–323.Google Scholar
[PhR1] Phillips, J. and Raeburn, I., Automorphisms of C-algebras and second Čech cohomology, Indiana Univ. Math. J. 29(1990), 799–822.Google Scholar
[PhR2] Phillips, J. and Raeburn, I., Crossed products by locally unitary automorphism groups and principal bundles, J. Operator Theory 11(1984), 215–241.Google Scholar
[RR] Raeburn, I. and Rosenberg, J., Crossed products of continuous trace C*-algebras by smooth actions, Trans. Amer. Math. Soc. 305(1988), 1–45.Google Scholar
[RW1] Raeburn, I. and Williams, D., Moore cohomology, principal bundles, and actions of groups on C*- algebras, Indiana Univ. Math. J. 40(1991), 707–740.Google Scholar
[RW2] Raeburn, I., Dixmier-Douady classes of dynamical systems and crossed products, Canad. J. Math., 45 (1993. 1032–1066.Google Scholar
[Ro] Rosenberg, J., Some results on cohomology with Borel cochains, with applications to groups actions on operator algebras. In: Advances on Invariant Subspaces and Other Results, Operator Theory, Adv. Appl. 17, Birkhauser, Basel, Boston, 1986. 301–330.Google Scholar
[Sm1] Smith, H., Commutative twisted group algebras, Trans. Amer. Math. Soc. 197(1974), 315–326.Google Scholar
[Sm2] Smith, H., Characteristic principal bundles, Trans. Amer. Math. Soc. 211(1975), 365–375.Google Scholar
[Sm3] Smith, H., Central twisted group algebras, Trans. Amer. Math. Soc. 238(1978), 309–320.Google Scholar
[V] Vick, J., Homology Theory. Academic Press, New York, San Francisco, London, 1973.Google Scholar