Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-15T11:23:27.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture

Part of: General theory of categories and functors Abelian categories Representation theory of rings and algebras Modules, bimodules and ideals

Published online by Cambridge University Press:  09 January 2025

Ziba Fazelpour  and
Alireza Nasr-Isfahani Open the ORCID record for Alireza Nasr-Isfahani [Opens in a new window]
Ziba Fazelpour
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran e-mail: [email protected]
Alireza Nasr-Isfahani*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Statistics, University of Isfahan, P.O. Box: 81746-73441, Isfahan, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran
*
e-mail: [email protected] [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate locally finitely presented pure semisimple (hereditary) Grothendieck categories. We show that every locally finitely presented pure semisimple (resp., hereditary) Grothendieck category $\mathscr {A}$ is equivalent to the category of left modules over a left pure semisimple (resp., left hereditary) ring when $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in 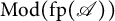$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. In fact, we show that there exists a bijection between Morita equivalence classes of left pure semisimple (resp., left hereditary) rings $\Lambda $ and equivalence classes of locally finitely presented pure semisimple (resp., hereditary) Grothendieck categories 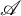$\mathscr {A}$ that $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in 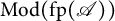$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. To prove this result, we study left pure semisimple rings by using Auslander’s ideas. We show that there exists, up to equivalence, a bijection between the class of left pure semisimple rings and the class of rings with nice homological properties. These results extend the Auslander and Ringel–Tachikawa correspondence to the class of left pure semisimple rings. As a consequence, we give several equivalent statements to the pure semisimplicity conjecture.

Keywords

Locally finitely presented categoryGrothendieck categorypure semisimple category

MSC classification

Primary: 18A25: Functor categories, comma categories 18E10: Exact categories, abelian categories 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation 16G60: Representation type (finite, tame, wild, etc.)
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the first author was in part supported by a grant from IPM. Also, the research of the second author was in part supported by a grant from IPM (No. 1403160416). The work of the second author is based upon research funded by Iran National Science Foundation (INSF) under project No. 4001480.

Dedicated to the memory of Daniel Simson

References

Albu, T. and Wisbauer, R., Generators in Grothendieck categories with right perfect endomorphism rings . Osaka J. Math. 28(1991), no. 2, 295–304.Google Scholar
Anderson, F. W., Fuller, K. R., Rings and Categories of Modules, second edition, Grad. Texts in Math., vol. 13, Springer-Verlag, New York, 1992.Google Scholar
Ánh, P. N. and Márki, L., Morita equivalence for rings without identity . Tsukuba J. Math. 11(2) (1987), 1–16.Google Scholar
Auslander, M., Large modules over artin algebras . In: Algebra, Topology and Category Theory. Academic Press (1976), 1–17.Google Scholar
Auslander, M., Representation theory of artin algebras I . Comm. Algebra 1(1974), 177–268.CrossRefGoogle Scholar
Auslander, M., Representation theory of artin algebras II . Comm. Algebra 1(1974), 269–310.CrossRefGoogle Scholar
Auslander, M., Reiten, I. and Smal, S. O. , Representation Theory of Artin Algebras. Cambridge Stud. Adv. Math. vol. 36, Cambridge Univ. Press, Cambridge, 1995.Google Scholar
Colby, R. R. and Rutter, E. A. Jr., Generalizations of QF-3 algebras . Trans. Am. Math. Soc. 153(1971), 371–386.Google Scholar
Colby, R. R. and Rutter, E. A. Jr., QF-3 rings with zero singular ideal . Pac. J. Math. 28(1969), 303–308.CrossRefGoogle Scholar
Crawley-Boevey, W., Locally finitely presented additive categories . Comm. Algebra 22(1994), no. 5, 1641–1674.CrossRefGoogle Scholar
Drozdowski, G. and Simson, D., Quivers of pure semi-simple type . Bull. Acad. Pol. Sci., Sér. Sci. Math. 27(1979), 33–40.Google Scholar
Dung, N. V. and García, J. L. Additive categories of locally finite representation type . J. Algebra 238(2001), no. 1, 200–238.CrossRefGoogle Scholar
Estrada, S. and Saorin, M., Locally finitely presented categories with no flat objects . Forum Math. 27(1) (2015) 269–301.CrossRefGoogle Scholar
Faith, C., Lecture on injective modules and quotient rings. Lecture Notes in Mathematics, 49. Springer-Verlag, Berlin-Heidelberg-New York, xv, 140 p. (1967).CrossRefGoogle Scholar
Fazelpour, Z. and Nasr-Isfahani, A., Finiteness and purity of subcategories of the module categories, arXiv:2203.03294.Google Scholar
Fazelpour, Z. and Nasr-Isfahani, A., Morita equivalence and Morita duality for rings with local units and the subcategory of projective unitary modules . Appl. Categ. Struct. 32(2024), no. 2, Paper No. 10, 28 p.CrossRefGoogle Scholar
Fuller, K. R., On rings whose left modules are direct sums of finitely generated modules . Proc. Am. Math. Soc. 54(1976), 39–44.CrossRefGoogle Scholar
Fuller, K. R. and Hullinger, H., Rings with finiteness conditions and their categories of functors . J. Algebra 55(1978), 94–105.CrossRefGoogle Scholar
Fuller, K. R. and Reiten, I., Note on rings of finite representation type and decompositions of modules . Proc. Am. Math. Soc. 50(1975), 92–94.CrossRefGoogle Scholar
Gabriel, P., Des catégories abéliennes . Bull. Soc. Math. Fr., 90(1962), 323–448.CrossRefGoogle Scholar
Gabriel, P., Indecomposable representations I . Manuscr. Math., 6(1972), 71–103.CrossRefGoogle Scholar
Gabriel, P., Indecomposable representations II . Symposia Math., 11(1973), 81–104.Google Scholar
Garcia, J. L. and Simson, D., On rings whose flat modules form a Grothendieck category . Colloq. Math. 73(1997), no. 1, 115–141.CrossRefGoogle Scholar
Garcia, J. L. and Simson, D., Structure theorems for pure semisimple Grothendieck locally PI-categories . Commun. Algebra 30(2002), no. 3, 1153–1197.CrossRefGoogle Scholar
Grothendieck, A., Sur quelques points d’algebre homologique . Tohoku Math. J. (2) 9(1957), 119–221.Google Scholar
Grothendieck, A. and Dieudonné, J. A., Elements de Géometrie Algébrique I . Grundlehren Math. Wiss. 166(1971).Google Scholar
Harada, M., Perfect categories I . Osaka J. Math. 10(1973), 329–341.Google Scholar
Harada, M., Perfect categories III: Hereditary and QF-3 categories . Osaka J. Math. 10(1973), 357–367.Google Scholar
Hullinger, H. L., Stable equivalence and rings whose modules are a direct sum of finitely generated modules . J. Pure Appl. Algebra 16(1980), 265–273.CrossRefGoogle Scholar
Hungerford, T. W., Algebra. Springer-Verlag Graduate Texts in Mathematics, vol. 73, 1974.CrossRefGoogle Scholar
Herzog, I., A test for finite representation type . J. Pure Appl. Algebra 95(1994), no. 2, 151–182.CrossRefGoogle Scholar
Krause, H., The spectrum of a module category . Mem. Am. Math. Soc. 707(2001), x+125 pp.Google Scholar
Kosakowska, J. and Simson, D., Hereditary coalgebras and representations of species . J. Algebra 293(2005), no. 2, 457–505.CrossRefGoogle Scholar
Menini, C., Gabriel-Popescu Type Theorems and Graded Modules, Perspectives in ring theory. In Proc. NATO Adv. Res. Workshop, Antwerp/Belg. 1987, NATO ASI Ser., Ser. C 233 (1988), 239–251.Google Scholar
Nowak, S. and Simson, D., Locally Dynkin quivers and hereditary coalgebras whose left comodules are direct sums of finite dimensional comodules . Comm. Algebra 30(2002), 455–476.CrossRefGoogle Scholar
Ringel, C. M. and Tachikawa, H., QF-3 rings . J. Reine Angew. Math. 272(1975), 49–72.Google Scholar
Simson, D., Coalgebras, comodules, pseudocompact algebras and tame comodule type . Colloq. Math. 90(2001), no. 1, 101–150.CrossRefGoogle Scholar
Simson, D., Functor categories in which every flat object is projective . Bull. Acad. Pol. Sci. Sér. Sci. Math. Astron. Phys. 22(1974), 375–380.Google Scholar
Simson, D., On pure global dimension of locally finitely presented Grothendieck categories . Fundam. Math. 96(1977), 91–116.CrossRefGoogle Scholar
Simson, D., On pure semi-simple Grothendieck categories I . Fundam. Math. 100(1978), 211–222.CrossRefGoogle Scholar
Simson, D., On pure semi-simple Grothendieck categories II . Fundam. Math. 110(1980), 107–116.CrossRefGoogle Scholar
Simson, D., On the structure of locally finite pure semisimple Grothendieck categories . Cah. Topol. Géom. Différ. 23(1982), 397–406.Google Scholar
Simson, D., Path coalgebras of quivers with relations and a tame-wild dichotomy problem for coalgebras, Lecture Notes in Pure and Appl. Math., Marcel-Dekker, vol. 236(2004), 465–492.Google Scholar
Simson, D., Pure semisimple categories and rings of finite representation type . J. Algebra 48(1977), 290–295.CrossRefGoogle Scholar
Simson, D., Pure semisimple categories and rings of finite representation type, Corrigendum. J. Algebra 67(1980), 254–256.CrossRefGoogle Scholar
Stenström, B., Rings of Quotients. An Introduction to Methods of Ring Theory, Die Grundlehren der mathematischen Wissenschaften. Band 217. Berlin-Heidelberg-New York: Springer-Verlag. VIII, 309 p.Google Scholar
Tachikawa, H., Quasi-Frobenius rings and generalizations. QF-3 and QF-1 rings . Notes by Claus Michael Ringel. Lecture Notes in Mathematics. Berlin-Heidelberg-New York: Springer-Verlag. XI, 351, 172 p.Google Scholar
Wisbauer, R., Foundations of Module and Ring Theory. A Handbook for Study and Research, Algebra Logic Appl., vol. 3, Gordon and Breach Science Publishers, Philadelphia, PA, 1991, revised and translated from the 1988 German edition.Google Scholar
Wisbauer, R., Zur Brauer-Thrall-Vermutung für Ringe . Arch. Math. 44(1985), 138–146.CrossRefGoogle Scholar
Yamagata, K., On Morita duality for additive group valued functors . Comm. Algebra 7(1979), 367–392.CrossRefGoogle Scholar
Huisgen-Zimmermann, B., Purity, algebraic compactness, direct sum decompositions, and representation type. In: Krause, H. and Ringel, C. M. (eds.), Infinite Length Modules, Bielefeld, 1998, pp. 331–367. Birkhäuser, Basel, 2000.Google Scholar