Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:17:06.026Z Has data issue: false hasContentIssue false
  • English
  • Français

L-Indistinguishability For SL (2)

Published online by Cambridge University Press:  20 November 2018

J-P. Labesse  and
R. P. Langlands
J-P. Labesse
Affiliation:
Faculté des Sciences, Dijon, France
R. P. Langlands
Affiliation:
The Institute for Advanced Study, Princeton, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The notion of L-indistinguishability, like many others current in the study of L-functions, has yet to be completely defined, but it is in our opinion important for the study of automorphic forms and of representations of algebraic groups. In this paper we study it for the simplest class of groups, basically forms of SL(2). Although the definition we use is applicable to very few groups, there is every reason to believe that the results will have general analogues [12].

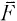The phenomena which the notion is intended to express have been met–and exploited–by others (Hecke [5] § 13, Shimura [17]). Their source seems to lie in the distinction between conjugacy and stable conjugacy. If F is a field, G a reductive algebraic group over F, and the algebraic closure of F then two elements of G(F) may be conjugate in 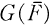without being conjugate in G(F).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 4 , 01 August 1979 , pp. 726 - 785
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Arthur, J., The Selberg trace formula for groups of F-rank one, Ann. of Math. 100 (1974).Google Scholar
2. Borel, A., Formes automorphes et séries de Dirichlet , Sem. Bourbaki (1975).Google Scholar
3. Duflo, M. et Labesse, J-P., Sur la formule des traces de Selberg, Ann. Se. de l'Ec. Norm. Sup. t. 4(1971).Google Scholar
4. Harish-Chandra, , Some results on an invariant integral on a semi-simple Lie algebra, Ann. of Math. 80 (1964).Google Scholar
5. Hecke, E., Uber Modulfunktionen und die Dirichletschen Reihen mit Eulerscher Produktentwicklung, II, Math. Ann. Bd. 114 (1937).Google Scholar
6. Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Lecture notes in mathematics 114 (1970).Google Scholar
7. Knapp, A. W. and Zuckerman, G., Classification of irreducible tempered representations of semisimple Lie groups, PNAS vol. 73 (1976).Google Scholar
8. Labesse, J. P., L-indistinguishable representations and the trace formula for SL(2), in Lie groups and their representations (John Wiley, 1975).Google Scholar
9. Langlands, R. P., Modular forms and l-adic representations, in Modular functions of one variable II, Lecture notes in mathematics 349 (1973).Google Scholar
10. Langlands, R. P., On the classification of irreducible representations of real algebraic groups, Notes, IAS (1973).Google Scholar
11. Langlands, R. P., Base change for GL(2), Notes, IAS (1975).Google Scholar
12. Langlands, R. P., Stable conjugacy: definitions and lemmas , to appear, Can. J. Math.Google Scholar
13. Langlands, R. P., On Artin s L-functions, Rice University Studies 56 (1970).Google Scholar
14. Langlands, R. P., Representations of abelian algebraic groups, Preprint, Yale (1968).Google Scholar
15. Langlands, R. P., Automorphic representations, Shimura varieties, and motives, to appear in Proc. Summer Institute, Corvallis (1977).Google Scholar
16. Shelstad, D., Notes on L-indistinguishability, to appear in Proc. Summer Institute, Corvallis (1977).Google Scholar
17. Shimura, G., On the factors of the jacobian variety of a modular function field, Jour. Math. Soc. Japan 25 (1973).Google Scholar
18. Tunnell, G., Langlands’ conjecture for GL(2) over local fields , to appear in Proc. Summer Institute, Corvallis (1977).Google Scholar