Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hayashi, Nakao
and
Naumkin †, Pavel I.
2004.
On the asymptotics for cubic nonlinear Schrödinger equations.
Complex Variables, Theory and Application: An International Journal,
Vol. 49,
Issue. 5,
p.
339.
SUNAGAWA, Hideaki
2006.
Large time behavior of solutions to the Klein-Gordon equation with nonlinear dissipative terms.
Journal of the Mathematical Society of Japan,
Vol. 58,
Issue. 2,
Hayashi, Nakao
Naumkin, Pavel I.
and
Sunagawa, Hideaki
2008.
On the Schrödinger Equation with Dissipative Nonlinearities of Derivative Type.
SIAM Journal on Mathematical Analysis,
Vol. 40,
Issue. 1,
p.
278.
Hayashi, Nakao
and
Naumkin, Pavel I.
2009.
Asymptotics of odd solutions for cubic nonlinear Schrödinger equations.
Journal of Differential Equations,
Vol. 246,
Issue. 4,
p.
1703.
I. Naumkin, Pavel
and
Sánchez-Suárez, Isahi
2011.
On the critical nongauge invariant nonlinear Schrödinger equation.
Discrete & Continuous Dynamical Systems - A,
Vol. 30,
Issue. 3,
p.
807.
Hayashi, Nakao
and
Naumkin, Pavel I.
2015.
Logarithmic Time Decay for the Cubic Nonlinear Schrödinger Equations.
International Mathematics Research Notices,
Vol. 2015,
Issue. 14,
p.
5604.
Sagawa, Yuji
and
Sunagawa, Hideaki
2016.
The lifespan of small solutions to cubic derivative nonlinear Schrödinger equations in one space dimension.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 10,
p.
5743.
Murphy, Jason
and
Pusateri, Fabio
2017.
Almost global existence for cubic nonlinear Schrödinger equations in one space dimension.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 4,
p.
2077.
Naumkin, Ivan
2018.
Nonlinear Schrödinger equations with exceptional potentials.
Journal of Differential Equations,
Vol. 265,
Issue. 9,
p.
4575.
Masaki, Satoshi
and
Miyazaki, Hayato
2018.
Long Range Scattering for Nonlinear Schrödinger Equations with Critical Homogeneous Nonlinearity.
SIAM Journal on Mathematical Analysis,
Vol. 50,
Issue. 3,
p.
3251.
Cazenave, Thierry
and
Naumkin, Ivan
2018.
Modified scattering for the critical nonlinear Schrödinger equation.
Journal of Functional Analysis,
Vol. 274,
Issue. 2,
p.
402.
Cazenave, Thierry
and
Naumkin, Ivan
2018.
Spatial behavior for NLS and applications to scattering.
Séminaire Laurent Schwartz — EDP et applications,
p.
1.
Naumkin, Ivan
2020.
Modified scattering for the mixed initial-boundary problem for the nonlinear Klein–Gordon equation.
Nonlinearity,
Vol. 33,
Issue. 1,
p.
276.
Li, Chunhua
Nishii, Yoshinori
Sagawa, Yuji
and
Sunagawa, Hideaki
2021.
On the derivative nonlinear Schrödinger equation with weakly dissipative structure.
Journal of Evolution Equations,
Vol. 21,
Issue. 2,
p.
1541.
El-Nabulsi, Rami Ahmad
2021.
Extended Ginzburg-Landau equations and Abrikrosov vortex and geometric transition from square to rectangular lattice in a magnetic field.
Physica C: Superconductivity and its Applications,
Vol. 581,
Issue. ,
p.
1353808.
Ballesteros, Miguel
Iniesta, Diego
Naumkin, Ivan
and
Peña, Clemente
2023.
Wave and scattering operators for the nonlinear matrix Schrödinger equation on the half-line with a potential.
Nonlinear Analysis,
Vol. 227,
Issue. ,
p.
113183.
Kawamoto, Masaki
and
Miyazaki, Hayato
2023.
Long-range scattering for a critical homogeneous type nonlinear Schrödinger equation with time-decaying harmonic potentials.
Journal of Differential Equations,
Vol. 365,
Issue. ,
p.
127.
Naumkin, Ivan
and
Weder, Ricardo
2023.
The matrix nonlinear Schrödinger equation with a potential.
Journal de Mathématiques Pures et Appliquées,
Vol. 172,
Issue. ,
p.
1.
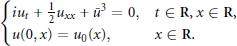 $$\left\{ \begin{align}
& i{{u}_{t}}\,+\,\frac{1}{2}{{u}_{xx}}\,+\,{{{\bar{u}}}^{3}}\,=\,0,\,\,\,\,\,t\,\in \,\mathbf{R},\,x\,\in \,\mathbf{R}, \\
& u(0,\,x)\,=\,{{u}_{0}}(x),\,\,\,\,\,\,\,\,\,\,\,x\,\in \,\mathbf{R}. \\
\end{align} \right.$$
$$\left\{ \begin{align}
& i{{u}_{t}}\,+\,\frac{1}{2}{{u}_{xx}}\,+\,{{{\bar{u}}}^{3}}\,=\,0,\,\,\,\,\,t\,\in \,\mathbf{R},\,x\,\in \,\mathbf{R}, \\
& u(0,\,x)\,=\,{{u}_{0}}(x),\,\,\,\,\,\,\,\,\,\,\,x\,\in \,\mathbf{R}. \\
\end{align} \right.$$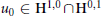 ${{u}_{0}}\,\in \,{{\mathbf{H}}^{1,\,0}}\,\cap \,{{\mathbf{H}}^{0,\,1}}$ are small and such that
${{u}_{0}}\,\in \,{{\mathbf{H}}^{1,\,0}}\,\cap \,{{\mathbf{H}}^{0,\,1}}$ are small and such that 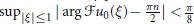 ${{\sup }_{|\xi |\le 1}}\left| \arg \mathcal{F}{{u}_{0}}(\text{ }\xi \text{ )}\text{0}\frac{\pi n}{2} \right|<\frac{\pi }{8}$ for some n ∈ Z, and
${{\sup }_{|\xi |\le 1}}\left| \arg \mathcal{F}{{u}_{0}}(\text{ }\xi \text{ )}\text{0}\frac{\pi n}{2} \right|<\frac{\pi }{8}$ for some n ∈ Z, and 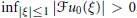 ${{\inf }_{\left| \xi \right|\le 1}}\,\left| \mathcal{F}{{u}_{0}}(\xi ) \right|\,>\,0$, then the solution has an additional logarithmic timedecay in the short range region
${{\inf }_{\left| \xi \right|\le 1}}\,\left| \mathcal{F}{{u}_{0}}(\xi ) \right|\,>\,0$, then the solution has an additional logarithmic timedecay in the short range region 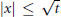 $\left| x \right|\,\le \,\sqrt{t}$. In the far region
$\left| x \right|\,\le \,\sqrt{t}$. In the far region 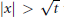 $\left| x \right|\,>\,\sqrt{t}$ the asymptotics have a quasilinear character.
$\left| x \right|\,>\,\sqrt{t}$ the asymptotics have a quasilinear character.