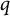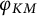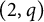1 Introduction
Let
![]() $(V,Q)$
be a quadratic space over
$(V,Q)$
be a quadratic space over
![]() $\mathbb {Q}$
of signature
$\mathbb {Q}$
of signature
![]() $(p,q)$
, and let G be its orthogonal group. Let
$(p,q)$
, and let G be its orthogonal group. Let
![]() $\mathbb {D}$
be the space of oriented negative q-planes in
$\mathbb {D}$
be the space of oriented negative q-planes in
![]() $V(\mathbb {R})$
and
$V(\mathbb {R})$
and
![]() $\mathbb {D}^+$
one of its connected components. It is a Riemannian manifold of dimension
$\mathbb {D}^+$
one of its connected components. It is a Riemannian manifold of dimension
![]() $pq$
and an open subset of the Grassmannian. The Lie group
$pq$
and an open subset of the Grassmannian. The Lie group
![]() $G(\mathbb {R})^+$
is the connected component of the identity and acts transitively on
$G(\mathbb {R})^+$
is the connected component of the identity and acts transitively on
![]() $\mathbb {D}^+$
. Hence, we can identify
$\mathbb {D}^+$
. Hence, we can identify
![]() $\mathbb {D}^+$
with
$\mathbb {D}^+$
with
![]() $G(\mathbb {R})^+ /K $
, where K is a compact subgroup of
$G(\mathbb {R})^+ /K $
, where K is a compact subgroup of
![]() $G(\mathbb {R})^+$
and is isomorphic to
$G(\mathbb {R})^+$
and is isomorphic to
![]() $\operatorname {SO}(p)\times \operatorname {SO}(q)$
. Moreover, let L be a lattice in
$\operatorname {SO}(p)\times \operatorname {SO}(q)$
. Moreover, let L be a lattice in
![]() $ V(\mathbb {Q}),$
and let
$ V(\mathbb {Q}),$
and let
![]() $\Gamma $
be a torsion-free subgroup of
$\Gamma $
be a torsion-free subgroup of
![]() $G(\mathbb {R})^+$
preserving L.
$G(\mathbb {R})^+$
preserving L.
For every vector v in
![]() $V(\mathbb {R})$
such that
$V(\mathbb {R})$
such that
![]() $Q(v,v)>0$
, there is a totally geodesic submanifold
$Q(v,v)>0$
, there is a totally geodesic submanifold
![]() $\mathbb {D}^+_v$
of codimension q consisting of all the negative q-planes that are orthogonal to v. Let
$\mathbb {D}^+_v$
of codimension q consisting of all the negative q-planes that are orthogonal to v. Let
![]() $\Gamma _v$
denote the stabilizer of v in
$\Gamma _v$
denote the stabilizer of v in
![]() $\Gamma $
. We can view
$\Gamma $
. We can view
![]() $ \Gamma _v \backslash \mathbb {D}^+$
as a rank q vector bundle over
$ \Gamma _v \backslash \mathbb {D}^+$
as a rank q vector bundle over
![]() $\Gamma _v \backslash \mathbb {D}_v^+$
, so that the natural embedding
$\Gamma _v \backslash \mathbb {D}_v^+$
, so that the natural embedding
![]() $\Gamma _v \backslash \mathbb {D}_v^+ $
in
$\Gamma _v \backslash \mathbb {D}_v^+ $
in
![]() $ \Gamma _v \backslash \mathbb {D}^+$
is the zero section. In [Reference Kudla and Millson6], Kudla and Millson constructed a closed
$ \Gamma _v \backslash \mathbb {D}^+$
is the zero section. In [Reference Kudla and Millson6], Kudla and Millson constructed a closed
![]() $G(\mathbb {R})^+$
-invariant differential form
$G(\mathbb {R})^+$
-invariant differential form
where
![]() $G(\mathbb {R})^+$
acts on the Schwartz space
$G(\mathbb {R})^+$
acts on the Schwartz space
![]() $\mathscr {S}(V(\mathbb {R}))$
from the left by
$\mathscr {S}(V(\mathbb {R}))$
from the left by
![]() and on
and on
![]() $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$
from the right by
$\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$
from the right by
![]() . In particular,
. In particular,
![]() $\varphi _{KM}(v)$
is a
$\varphi _{KM}(v)$
is a
![]() $\Gamma _v$
-invariant form on
$\Gamma _v$
-invariant form on
![]() $\mathbb {D}^+$
. The main property of the Kudla–Millson form is its Thom form property: if
$\mathbb {D}^+$
. The main property of the Kudla–Millson form is its Thom form property: if
![]() $\omega $
in
$\omega $
in
![]() $\Omega _c^{pq-q}(\Gamma _v \backslash \mathbb {D}^+)$
is a compactly supported form, then
$\Omega _c^{pq-q}(\Gamma _v \backslash \mathbb {D}^+)$
is a compactly supported form, then
Another way to state it is to say that in cohomology, we have
where
![]() $\operatorname {PD}(\Gamma _v \backslash \mathbb {D}^+_v)$
denotes the Poincaré dual class to
$\operatorname {PD}(\Gamma _v \backslash \mathbb {D}^+_v)$
denotes the Poincaré dual class to
![]() $\Gamma _v \backslash \mathbb {D}^+_v$
.
$\Gamma _v \backslash \mathbb {D}^+_v$
.
1.1 Kudla–Millson theta lift
In order to motivate the interest in the Kudla–Millson form, let us briefly recall how it is used to construct a theta correspondence between certain cohomology classes and modular forms. For simplicity,Footnote
1
assume that
![]() $p+q$
is even, and let
$p+q$
is even, and let
![]() $\omega $
be the Weil representation of the dual pair
$\omega $
be the Weil representation of the dual pair
![]() $\operatorname {SL}_2(\mathbb {R}) \times G(\mathbb {R})$
in
$\operatorname {SL}_2(\mathbb {R}) \times G(\mathbb {R})$
in
![]() $\mathscr {S}(V(\mathbb {R}))$
. We extend it to a representation in
$\mathscr {S}(V(\mathbb {R}))$
. We extend it to a representation in
![]() $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$
by acting in the second factor of the tensor product. Building on the work of [Reference Weil11], Kudla and Millson [Reference Kudla and Millson7, Reference Kudla and Millson9] used their differential form to construct the theta series
$\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$
by acting in the second factor of the tensor product. Building on the work of [Reference Weil11], Kudla and Millson [Reference Kudla and Millson7, Reference Kudla and Millson9] used their differential form to construct the theta series
where
![]() $\tau =x+iy$
is in
$\tau =x+iy$
is in
![]() $\mathbb {H}$
and
$\mathbb {H}$
and
![]() $g_\tau $
is the matrix
$g_\tau $
is the matrix
 $\begin {pmatrix} \sqrt {y} & x\sqrt {y}^{-1} \\ 0 & \sqrt {y}^{-1} \end {pmatrix}$
in
$\begin {pmatrix} \sqrt {y} & x\sqrt {y}^{-1} \\ 0 & \sqrt {y}^{-1} \end {pmatrix}$
in
![]() $\operatorname {SL}_2(\mathbb {R})$
that sends i to
$\operatorname {SL}_2(\mathbb {R})$
that sends i to
![]() $\tau $
by Möbius transformation. This form is
$\tau $
by Möbius transformation. This form is
![]() $\Gamma $
-invariant, closed and holomorphic in cohomology in the sense that
$\Gamma $
-invariant, closed and holomorphic in cohomology in the sense that
![]() $\frac {\partial }{\partial \overline {\tau }}\Theta _{KM}(\tau )$
is an exact form. Kudla and Millson showed that if we integrate this closed form on a compact q-cycle C in
$\frac {\partial }{\partial \overline {\tau }}\Theta _{KM}(\tau )$
is an exact form. Kudla and Millson showed that if we integrate this closed form on a compact q-cycle C in
![]() $\mathcal {Z}_q(\Gamma \backslash \mathbb {D}^+)$
, then
$\mathcal {Z}_q(\Gamma \backslash \mathbb {D}^+)$
, then
is a modular form of weight
![]() $\frac {p+q}{2}$
, where
$\frac {p+q}{2}$
, where

and the special cycles
![]() $C_v$
are the images of the composition
$C_v$
are the images of the composition
Thus, the Kudla–Millson theta series realizes a lift between the (co)-homology of
![]() $\Gamma \backslash \mathbb {D}^+$
and the space of weight
$\Gamma \backslash \mathbb {D}^+$
and the space of weight
![]() $\frac {p+q}{2}$
modular forms.
$\frac {p+q}{2}$
modular forms.
1.2 The result
Let E be a
![]() $G(\mathbb {R})^+$
-equivariant vector bundle of rank q over
$G(\mathbb {R})^+$
-equivariant vector bundle of rank q over
![]() $\mathbb {D}^+$
, and let
$\mathbb {D}^+$
, and let
![]() $E_0$
be the image of the zero section. By the equivariance, we also have a vector bundle
$E_0$
be the image of the zero section. By the equivariance, we also have a vector bundle
![]() $\Gamma _v \backslash E$
over
$\Gamma _v \backslash E$
over
![]() $\Gamma _v \backslash \mathbb {D}^+$
. The Thom class of the vector bundle is a characteristic class
$\Gamma _v \backslash \mathbb {D}^+$
. The Thom class of the vector bundle is a characteristic class
![]() $\operatorname {Th}(\Gamma _v \backslash E)$
in
$\operatorname {Th}(\Gamma _v \backslash E)$
in
![]() $ H^{q}(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$
defined by the Thom isomorphism (see Section 3.6). A Thom form is a form representing the Thom class. It can be shown that the Thom class is also the Poincaré dual class to
$ H^{q}(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$
defined by the Thom isomorphism (see Section 3.6). A Thom form is a form representing the Thom class. It can be shown that the Thom class is also the Poincaré dual class to
![]() $\Gamma _v \backslash E_0$
. Let
$\Gamma _v \backslash E_0$
. Let
![]() $s_v \colon \Gamma _v \backslash \mathbb {D}^+ \longrightarrow \Gamma _v \backslash E$
be a section whose zero locus is
$s_v \colon \Gamma _v \backslash \mathbb {D}^+ \longrightarrow \Gamma _v \backslash E$
be a section whose zero locus is
![]() $\Gamma _v \backslash \mathbb {D}_v^+$
, then
$\Gamma _v \backslash \mathbb {D}_v^+$
, then
Viewing it as a class in
![]() $H^q(\Gamma _v \backslash \mathbb {D}^+)$
it is the Poincaré dual class of
$H^q(\Gamma _v \backslash \mathbb {D}^+)$
it is the Poincaré dual class of
![]() $\Gamma _v \backslash \mathbb {D}_v^+$
. Since the Poincaré dual class is unique, property (1.3) implies that
$\Gamma _v \backslash \mathbb {D}_v^+$
. Since the Poincaré dual class is unique, property (1.3) implies that
on the level of cohomology.
For arbitrary real oriented metric vector bundles, Mathai and Quillen used the Chern–Weil theory to construct in [Reference Mathai and Quillen10] a canonical Thom form on E. We denote by
![]() $U_{MQ}$
the canonical Thom form in
$U_{MQ}$
the canonical Thom form in
![]() $\Omega ^{q}(E)$
of Mathai and Quillen. Since
$\Omega ^{q}(E)$
of Mathai and Quillen. Since
![]() $U_{MQ}$
is
$U_{MQ}$
is
![]() $\Gamma $
-invariant, it is also a Thom form for the bundle
$\Gamma $
-invariant, it is also a Thom form for the bundle
![]() $\Gamma _v \backslash E$
for every vector v. The main result is the following.
$\Gamma _v \backslash E$
for every vector v. The main result is the following.
Theorem (Theorem 4.5)
For a natural choice of a bundle E and of a section
![]() $s_v$
, we have
$s_v$
, we have
![]() $\varphi _{KM}(v)= 2^{-\frac {q}{2}}e^{-\pi Q(v,v)} s_v^\ast U_{MQ}$
in
$\varphi _{KM}(v)= 2^{-\frac {q}{2}}e^{-\pi Q(v,v)} s_v^\ast U_{MQ}$
in
![]() $\Omega ^q(\Gamma _v \backslash \mathbb {D}^+).$
$\Omega ^q(\Gamma _v \backslash \mathbb {D}^+).$
The bundle E is the tautological bundle of the Grassmannian
![]() $\mathbb {D}^+$
(see Section 3.6), and the section
$\mathbb {D}^+$
(see Section 3.6), and the section
![]() $s_v$
is defined in Section 4.1.
$s_v$
is defined in Section 4.1.
For signature
![]() $(2,q)$
, the spaces are Hermitian and the result was obtained by a similar method in [Reference Garcia3] using the work of Bismut–Gillet–Soulé.
$(2,q)$
, the spaces are Hermitian and the result was obtained by a similar method in [Reference Garcia3] using the work of Bismut–Gillet–Soulé.
1.3 Generalizations
More generally, for a positive nondegenerate r-subspace
![]() $U \subset V$
spanned by vectors
$U \subset V$
spanned by vectors
![]() $v_1, \dots , v_r$
, Kudla and Millson also construct an
$v_1, \dots , v_r$
, Kudla and Millson also construct an
![]() $rq$
form
$rq$
form
![]() $\varphi _{KM}(v_1,\dots ,v_r)$
. This form can also be recovered by the Mathai–Quillen formalism (see (3) of Section 5). Furthermore, in [Reference Kudla and Millson7, Reference Kudla and Millson9], they not only construct forms for the symmetric space associated with
$\varphi _{KM}(v_1,\dots ,v_r)$
. This form can also be recovered by the Mathai–Quillen formalism (see (3) of Section 5). Furthermore, in [Reference Kudla and Millson7, Reference Kudla and Millson9], they not only construct forms for the symmetric space associated with
![]() $\operatorname {SO}(p,q)$
, but also for the Hermitian space associated with
$\operatorname {SO}(p,q)$
, but also for the Hermitian space associated with
![]() $U(p,q)$
. In this case, one should be able to recover their forms using the formalism of superconnections as in [Reference Mathai and Quillen10, Theorem 8.5]. We expect the computations to be closer to the computations done in [Reference Garcia3].
$U(p,q)$
. In this case, one should be able to recover their forms using the formalism of superconnections as in [Reference Mathai and Quillen10, Theorem 8.5]. We expect the computations to be closer to the computations done in [Reference Garcia3].
2 The Kudla–Millson form
2.1 The symmetric space
 $\mathbb {D}$
$\mathbb {D}$
Let
![]() $(V,Q)$
be a rational quadratic space, and let
$(V,Q)$
be a rational quadratic space, and let
![]() $(p,q)$
be the signature of
$(p,q)$
be the signature of
![]() $V(\mathbb {R})$
. Let
$V(\mathbb {R})$
. Let
![]() $e_1, \dots , e_{p+q}$
be an orthogonal basis of
$e_1, \dots , e_{p+q}$
be an orthogonal basis of
![]() $V(\mathbb {R})$
such that
$V(\mathbb {R})$
such that
 $$ \begin{align} Q(e_\alpha , e_\alpha) =1 \quad & \textrm{for} \quad \; 1 \leq \alpha \leq p, \nonumber \\ Q(e_\mu , e_\mu) =-1 \quad & \textrm{for} \quad \; p+1 \leq \mu \leq p+q. \end{align} $$
$$ \begin{align} Q(e_\alpha , e_\alpha) =1 \quad & \textrm{for} \quad \; 1 \leq \alpha \leq p, \nonumber \\ Q(e_\mu , e_\mu) =-1 \quad & \textrm{for} \quad \; p+1 \leq \mu \leq p+q. \end{align} $$
Note that we will always use letters
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
for indices between
$\beta $
for indices between
![]() $1$
and p, and letters
$1$
and p, and letters
![]() $\mu $
and
$\mu $
and
![]() $\nu $
for indices between
$\nu $
for indices between
![]() $p+1$
and
$p+1$
and
![]() $p+q$
. A plane z in
$p+q$
. A plane z in
![]() $V(\mathbb {R})$
is a negative plane if
$V(\mathbb {R})$
is a negative plane if
![]() $Q\big|{}_{z} $
is negative definite. Let
$Q\big|{}_{z} $
is negative definite. Let
be the set of negative-oriented q-planes in
![]() $V(\mathbb {R})$
. For each negative plane, there are two possible orientations, yielding two connected components
$V(\mathbb {R})$
. For each negative plane, there are two possible orientations, yielding two connected components
![]() $\mathbb {D}^+ $
and
$\mathbb {D}^+ $
and
![]() $ \mathbb {D}^-$
of
$ \mathbb {D}^-$
of
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $z_0$
in
$z_0$
in
![]() $\mathbb {D}^+$
be the negative plane spanned by the vectors
$\mathbb {D}^+$
be the negative plane spanned by the vectors
![]() $e_{p+1}, \dots , e_{p+q}$
together with a fixed orientation. The group
$e_{p+1}, \dots , e_{p+q}$
together with a fixed orientation. The group
![]() $G(\mathbb {R})^+$
acts transitively on
$G(\mathbb {R})^+$
acts transitively on
![]() $\mathbb {D}^+$
by sending
$\mathbb {D}^+$
by sending
![]() $z_0$
to
$z_0$
to
![]() $gz_0$
. Let K be the stabilizer of
$gz_0$
. Let K be the stabilizer of
![]() $z_0$
, which is isomorphic to
$z_0$
, which is isomorphic to
![]() $\operatorname {SO}(p)\times \operatorname {SO}(q)$
. Thus, we have an identification
$\operatorname {SO}(p)\times \operatorname {SO}(q)$
. Thus, we have an identification
 $$ \begin{align} G(\mathbb{R})^+/K & \longrightarrow \mathbb{D}^+ \nonumber \\ gK & \longmapsto gz_0. \end{align} $$
$$ \begin{align} G(\mathbb{R})^+/K & \longrightarrow \mathbb{D}^+ \nonumber \\ gK & \longmapsto gz_0. \end{align} $$
For z in
![]() $\mathbb {D}^+$
, we denote by
$\mathbb {D}^+$
, we denote by
![]() $g_z$
any element of
$g_z$
any element of
![]() $G(\mathbb {R})^+$
sending
$G(\mathbb {R})^+$
sending
![]() $z_0$
to z.
$z_0$
to z.
For a positive vector v in
![]() $V(\mathbb {R}),$
we define
$V(\mathbb {R}),$
we define
It is a totally geodesic submanifold of
![]() $\mathbb {D}$
of codimension q. Let
$\mathbb {D}$
of codimension q. Let
![]() $\mathbb {D}_v^+$
be the intersection of
$\mathbb {D}_v^+$
be the intersection of
![]() $\mathbb {D}_v$
with
$\mathbb {D}_v$
with
![]() $\mathbb {D}^+$
.
$\mathbb {D}^+$
.
Let z in
![]() $\mathbb {D}^+$
be a negative plane. With respect to the orthogonal splitting of
$\mathbb {D}^+$
be a negative plane. With respect to the orthogonal splitting of
![]() $V(\mathbb {R})$
as
$V(\mathbb {R})$
as
![]() $z^\perp \oplus z$
, the quadratic form splits as
$z^\perp \oplus z$
, the quadratic form splits as
We define the Siegel majorant at z to be the positive-definite quadratic form
2.2 The Lie algebras
 $\mathfrak {g}$
and
$\mathfrak {g}$
and
 $\mathfrak {k}$
$\mathfrak {k}$
Let


be the Lie algebras of
![]() $G(\mathbb {R})^+$
and
$G(\mathbb {R})^+$
and
![]() $K,$
where
$K,$
where
![]() $\mathfrak {so}(z_0)$
is equal to
$\mathfrak {so}(z_0)$
is equal to
![]() $\mathfrak {so}(q)$
. The latter is the space of skew-symmetric q by q matrices. Similarly, we have
$\mathfrak {so}(q)$
. The latter is the space of skew-symmetric q by q matrices. Similarly, we have
![]() $\mathfrak {so}(z_0^\perp )$
equals
$\mathfrak {so}(z_0^\perp )$
equals
![]() $\mathfrak {so}(p)$
. Hence, we have a decomposition of
$\mathfrak {so}(p)$
. Hence, we have a decomposition of
![]() $\mathfrak {k}$
as
$\mathfrak {k}$
as
![]() $\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$
that is orthogonal with respect to the Killing form. Let
$\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$
that is orthogonal with respect to the Killing form. Let
![]() $\epsilon $
be the Lie algebra involution of
$\epsilon $
be the Lie algebra involution of
![]() $\mathfrak {g}$
mapping X to
$\mathfrak {g}$
mapping X to
![]() $-X$
. The
$-X$
. The
![]() $+1$
-eigenspace of
$+1$
-eigenspace of
![]() $\epsilon $
is
$\epsilon $
is
![]() $\mathfrak {k}$
and the
$\mathfrak {k}$
and the
![]() $-1$
-eigenspace is
$-1$
-eigenspace is

We have a decomposition of
![]() $\mathfrak {g} $
as
$\mathfrak {g} $
as
![]() $\mathfrak {k} \oplus \mathfrak {p}$
and it is orthogonal with respect to the Killing form. We can identify
$\mathfrak {k} \oplus \mathfrak {p}$
and it is orthogonal with respect to the Killing form. We can identify
![]() $\mathfrak {p}$
with
$\mathfrak {p}$
with
![]() $\mathfrak {g}/\mathfrak {k}$
. Since
$\mathfrak {g}/\mathfrak {k}$
. Since
![]() $\epsilon $
is a Lie algebra automorphism, we have that
$\epsilon $
is a Lie algebra automorphism, we have that
We identify the tangent space of
![]() $\mathbb {D}^+$
at
$\mathbb {D}^+$
at
![]() $eK$
with
$eK$
with
![]() $\mathfrak {p}$
and the tangent bundle
$\mathfrak {p}$
and the tangent bundle
![]() $T\mathbb {D}^+$
with
$T\mathbb {D}^+$
with
![]() $G(\mathbb {R})^+ \times _K \mathfrak {p}$
, where K acts on
$G(\mathbb {R})^+ \times _K \mathfrak {p}$
, where K acts on
![]() $\mathfrak {p}$
by the
$\mathfrak {p}$
by the
![]() $\operatorname {Ad}$
-representation. We have an isomorphism
$\operatorname {Ad}$
-representation. We have an isomorphism

A basis of
![]() $\mathfrak {g}$
is given by the set of matrices
$\mathfrak {g}$
is given by the set of matrices
and we denote by
![]() $\omega _{ij}$
, its dual basis in the dual space
$\omega _{ij}$
, its dual basis in the dual space
![]() $\mathfrak {g}^\ast $
. Let
$\mathfrak {g}^\ast $
. Let
![]() $E_{ij}$
be the elementary matrix sending
$E_{ij}$
be the elementary matrix sending
![]() $e_i$
to
$e_i$
to
![]() $e_j$
and the other
$e_j$
and the other
![]() $e_k$
’s to
$e_k$
’s to
![]() $0$
. Then
$0$
. Then
![]() $\mathfrak {p}$
is spanned by the matrices
$\mathfrak {p}$
is spanned by the matrices
and
![]() $\mathfrak {k}$
is spanned by the matrices
$\mathfrak {k}$
is spanned by the matrices
 $$ \begin{align} X_{\alpha \beta} & = E_{\alpha \beta}-E_{\beta \alpha}, \nonumber \\ X_{\nu \mu} & = -E_{\nu \mu}+E_{\mu \nu}. \end{align} $$
$$ \begin{align} X_{\alpha \beta} & = E_{\alpha \beta}-E_{\beta \alpha}, \nonumber \\ X_{\nu \mu} & = -E_{\nu \mu}+E_{\mu \nu}. \end{align} $$
2.3 Poincaré duals
Let M be an arbitrary m-dimensional real orientable manifold without boundary. The integration map yields a nondegenerate pairing [Reference Bott and Tu2, Theorem 5.11]
 $$ \begin{align} H^{q}(M) \otimes_{\mathbb{R}} H_c^{m-q}(M)& \longrightarrow \mathbb{R} \nonumber \\ [\omega]\otimes [\eta] & \longmapsto \int_M \omega \wedge \eta, \end{align} $$
$$ \begin{align} H^{q}(M) \otimes_{\mathbb{R}} H_c^{m-q}(M)& \longrightarrow \mathbb{R} \nonumber \\ [\omega]\otimes [\eta] & \longmapsto \int_M \omega \wedge \eta, \end{align} $$
where
![]() $H_c(M)$
denotes the cohomology of compactly supported forms on M. This yields an isomorphism between
$H_c(M)$
denotes the cohomology of compactly supported forms on M. This yields an isomorphism between
![]() $H^{q}(M)$
and the dual
$H^{q}(M)$
and the dual
![]() $H_c^{m-q}(M)^\ast =\operatorname {Hom}(H_c^{m-q}(M),\mathbb {R})$
. If C is an immersed submanifold of codimension q in M, then C defines a linear functional on
$H_c^{m-q}(M)^\ast =\operatorname {Hom}(H_c^{m-q}(M),\mathbb {R})$
. If C is an immersed submanifold of codimension q in M, then C defines a linear functional on
![]() $H_c^{m-q}(M)$
by
$H_c^{m-q}(M)$
by
Since we have an isomorphism between
![]() $H_c^{m-q}(M)^\ast $
and
$H_c^{m-q}(M)^\ast $
and
![]() $H^{q}(M)$
, there is a unique cohomology class
$H^{q}(M)$
, there is a unique cohomology class
![]() $\operatorname {PD}(C)$
in
$\operatorname {PD}(C)$
in
![]() $H^q(M)$
representing this functional, i.e.,
$H^q(M)$
representing this functional, i.e.,
for every class
![]() $[\omega ]$
in
$[\omega ]$
in
![]() $H_c^{m-q}(M)$
. We call
$H_c^{m-q}(M)$
. We call
![]() $\operatorname {PD}(C)$
the Poincaré dual class to C, and any differential form representing the cohomology class
$\operatorname {PD}(C)$
the Poincaré dual class to C, and any differential form representing the cohomology class
![]() $\operatorname {PD}(C)$
a Poincaré dual form to C.
$\operatorname {PD}(C)$
a Poincaré dual form to C.
2.4 The Kudla–Millson form
The tangent plane at the identity
![]() $T_{eK} \mathbb {D}^+ $
can be identified with
$T_{eK} \mathbb {D}^+ $
can be identified with
![]() $\mathfrak {p}$
and the cotangent bundle
$\mathfrak {p}$
and the cotangent bundle
![]() $(T\mathbb {D}^+)^\ast $
with
$(T\mathbb {D}^+)^\ast $
with
![]() $G(\mathbb {R})^+ \times _K \mathfrak {p}^\ast $
, where K acts on
$G(\mathbb {R})^+ \times _K \mathfrak {p}^\ast $
, where K acts on
![]() $\mathfrak {p}^\ast $
by the dual of the
$\mathfrak {p}^\ast $
by the dual of the
![]() $\operatorname {Ad}$
-representation. The basis
$\operatorname {Ad}$
-representation. The basis
![]() $e_1, \dots , e_{p+q}$
identifies
$e_1, \dots , e_{p+q}$
identifies
![]() $V(\mathbb {R})$
with
$V(\mathbb {R})$
with
![]() $\mathbb {R}^{p+q}$
. With respect to this basis, the Siegel majorant at
$\mathbb {R}^{p+q}$
. With respect to this basis, the Siegel majorant at
![]() $z_0$
is given by
$z_0$
is given by

Recall that
![]() $G(\mathbb {R})^+$
acts on
$G(\mathbb {R})^+$
acts on
![]() $\mathscr {S}(\mathbb {R}^{p+q})$
from the left by
$\mathscr {S}(\mathbb {R}^{p+q})$
from the left by
![]() $(g \cdot f)(v)= f(g^{-1}v)$
and on
$(g \cdot f)(v)= f(g^{-1}v)$
and on
![]() $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(\mathbb {R}^{p+q})$
from the right by
$\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(\mathbb {R}^{p+q})$
from the right by
![]() . We have an isomorphism
. We have an isomorphism
 $$ \begin{align} \left [ \Omega^q(\mathbb{D}^+) \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+} & \longrightarrow \left [ \sideset{}{^q}\bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^K \nonumber \\ \varphi & \longrightarrow \varphi_e \end{align} $$
$$ \begin{align} \left [ \Omega^q(\mathbb{D}^+) \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+} & \longrightarrow \left [ \sideset{}{^q}\bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^K \nonumber \\ \varphi & \longrightarrow \varphi_e \end{align} $$
by evaluating
![]() $\varphi $
at the basepoint
$\varphi $
at the basepoint
![]() $eK$
in
$eK$
in
![]() $G(\mathbb {R})^+/K$
, corresponding to the point
$G(\mathbb {R})^+/K$
, corresponding to the point
![]() $z_0$
in
$z_0$
in
![]() $\mathbb {D}^+$
. We define the Howe operator
$\mathbb {D}^+$
. We define the Howe operator
by

where
![]() $A_{\alpha \mu }$
denotes left multiplication by
$A_{\alpha \mu }$
denotes left multiplication by
![]() $\omega _{\alpha \mu }$
. The Kudla–Millson form is defined by applying D to the Gaussian:
$\omega _{\alpha \mu }$
. The Kudla–Millson form is defined by applying D to the Gaussian:
Kudla and Millson showed that this form is K-invariant. Hence, by the isomorphism (2.19), we get a form
In particular, since
![]() $g^\ast \varphi _{KM}(v)=\varphi _{KM}(g^{-1}v)$
for any
$g^\ast \varphi _{KM}(v)=\varphi _{KM}(g^{-1}v)$
for any
![]() $g \in G(\mathbb {R})^+$
, the form is
$g \in G(\mathbb {R})^+$
, the form is
![]() $\Gamma _v$
-invariant and defines a form on
$\Gamma _v$
-invariant and defines a form on
![]() $\Gamma _v \backslash \mathbb {D}^+$
. It is also closed and Kudla–Millson prove in [Reference Kudla and Millson8, Proposition 5.2] that it satisfies the Thom form property: for every compactly supported form
$\Gamma _v \backslash \mathbb {D}^+$
. It is also closed and Kudla–Millson prove in [Reference Kudla and Millson8, Proposition 5.2] that it satisfies the Thom form property: for every compactly supported form
![]() $\omega $
in
$\omega $
in
![]() $\Omega ^{pq-q}_c(\Gamma _v \backslash \mathbb {D}^+)$
, we have
$\Omega ^{pq-q}_c(\Gamma _v \backslash \mathbb {D}^+)$
, we have
3 The Mathai–Quillen formalism
We begin by recalling a few facts about principal bundles, connections, and associated vector bundles. For more details, we refer to [Reference Berline, Getzler and Vergne1, Reference Kobayashi and Nomizu5]. The Mathai–Quillen form is defined in Section 3.7 following [Reference Berline, Getzler and Vergne1] (see also [Reference Getzler, Cruzeiro and Zambrini4]).
3.1 K-principal bundles and principal connections
Let K be
![]() $\operatorname {SO}(p)\times \operatorname {SO}(q)$
as before, and let P be a smooth principal K-bundle. Let
$\operatorname {SO}(p)\times \operatorname {SO}(q)$
as before, and let P be a smooth principal K-bundle. Let
 $$ \begin{align} R \colon K \times P \longrightarrow P \nonumber \\ (k,p) \longmapsto R_k(p) \end{align} $$
$$ \begin{align} R \colon K \times P \longrightarrow P \nonumber \\ (k,p) \longmapsto R_k(p) \end{align} $$
be the smooth right action of K on P and
the projection map. For a fixed
![]() $p $
in P, consider the map
$p $
in P, consider the map
 $$ \begin{align} R_p \colon K & \longrightarrow P \nonumber \nonumber \\ k & \longmapsto R_k(p). \end{align} $$
$$ \begin{align} R_p \colon K & \longrightarrow P \nonumber \nonumber \\ k & \longmapsto R_k(p). \end{align} $$
Let
![]() $V_pP$
be the image of the derivative at the identity
$V_pP$
be the image of the derivative at the identity
which is injective. It coincides with the kernel of the differential
![]() $d_p\pi $
. A vector in
$d_p\pi $
. A vector in
![]() $V_pP$
is called a vertical vector. Using this map, we can view a vector X in
$V_pP$
is called a vertical vector. Using this map, we can view a vector X in
![]() $\mathfrak {k}$
as a vertical vector field on P. The space P can a priori be arbitrary, but in our case, we will consider either:
$\mathfrak {k}$
as a vertical vector field on P. The space P can a priori be arbitrary, but in our case, we will consider either:
-
(1) P is
 $G(\mathbb {R})^+$
and
$G(\mathbb {R})^+$
and
 $R_k$
the natural right action sending g to
$R_k$
the natural right action sending g to
 $gk$
. Then
$gk$
. Then
 $P/K$
can be identified with
$P/K$
can be identified with
 $\mathbb {D}^+$
.
$\mathbb {D}^+$
. -
(2) P is
 $G(\mathbb {R})^+ \times z_0$
and the action
$G(\mathbb {R})^+ \times z_0$
and the action
 $R_k$
maps
$R_k$
maps
 $(g,w)$
to
$(g,w)$
to
 $(gk,k^{-1}w)$
. In this case,
$(gk,k^{-1}w)$
. In this case,
 $P/K$
can be identified with
$P/K$
can be identified with
 $G(\mathbb {R})^+ \times _K z_0$
. It is the vector bundle associated with the principal bundle
$G(\mathbb {R})^+ \times _K z_0$
. It is the vector bundle associated with the principal bundle
 $G(\mathbb {R})^+$
as defined below.
$G(\mathbb {R})^+$
as defined below.
A principal K-connection on P is a
![]() $1$
-form
$1$
-form
![]() $\theta _P $
in
$\theta _P $
in
![]() $\Omega ^1(P, \mathfrak {k})$
such that:
$\Omega ^1(P, \mathfrak {k})$
such that:
-
•
 $\iota _X \theta _P = X$
for any
$\iota _X \theta _P = X$
for any
 $X $
in
$X $
in
 $\mathfrak {k}$
,
$\mathfrak {k}$
, -
•
 $R_k^\ast \theta _P=Ad(k^{-1}) \theta _P \quad $
for any k in K,
$R_k^\ast \theta _P=Ad(k^{-1}) \theta _P \quad $
for any k in K,
where
![]() $\iota _X$
is the interior product
$\iota _X$
is the interior product

and we view X as a vector field on P. Geometrically, these conditions imply that the kernel of
![]() $\theta _P$
defines a horizontal subspace of
$\theta _P$
defines a horizontal subspace of
![]() $TP$
that we denote by
$TP$
that we denote by
![]() $HP$
. It is a complement to the vertical subspace, i.e., we get a splitting of
$HP$
. It is a complement to the vertical subspace, i.e., we get a splitting of
![]() $T_pP$
as
$T_pP$
as
![]() $V_pP \oplus H_pP$
.
$V_pP \oplus H_pP$
.
Let
![]() $\mathfrak {g}$
be the Lie algebra of
$\mathfrak {g}$
be the Lie algebra of
![]() $G(\mathbb {R})^+$
, and let
$G(\mathbb {R})^+$
, and let
![]() $\mathcal {P}$
be the orthogonal projection from
$\mathcal {P}$
be the orthogonal projection from
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\mathfrak {k}$
. After identifying
$\mathfrak {k}$
. After identifying
![]() $\mathfrak {g}^\ast $
with the space
$\mathfrak {g}^\ast $
with the space
![]() $\Omega ^1(G(\mathbb {R})^+)^{G(\mathbb {R})^+}$
of
$\Omega ^1(G(\mathbb {R})^+)^{G(\mathbb {R})^+}$
of
![]() $G(\mathbb {R})^+$
-invariant forms, we define a natural
$G(\mathbb {R})^+$
-invariant forms, we define a natural
![]() $1$
-form
$1$
-form
called the Maurer–Cartan form, where
![]() $X_{ij}$
is the basis of
$X_{ij}$
is the basis of
![]() $\mathfrak {g}$
defined earlier and
$\mathfrak {g}$
defined earlier and
![]() $\omega _{ij}$
its dual in
$\omega _{ij}$
its dual in
![]() $\mathfrak {g}^\ast $
. After projection onto
$\mathfrak {g}^\ast $
. After projection onto
![]() $\mathfrak {k}$
, we get a form
$\mathfrak {k}$
, we get a form

where we identify
![]() $\Omega ^1(G(\mathbb {R})^+, \mathfrak {k})$
with
$\Omega ^1(G(\mathbb {R})^+, \mathfrak {k})$
with
![]() $\Omega ^1(G(\mathbb {R})^+) \otimes \mathfrak {k}$
. A direct computation shows that it is a principal K-connection on P, when P is
$\Omega ^1(G(\mathbb {R})^+) \otimes \mathfrak {k}$
. A direct computation shows that it is a principal K-connection on P, when P is
![]() $G(\mathbb {R})^+$
.
$G(\mathbb {R})^+$
.
If P is
![]() $G(\mathbb {R})^+ \times z_0$
, then the projection
$G(\mathbb {R})^+ \times z_0$
, then the projection
induces a pullback map
The form
is a principal connection on
![]() $G(\mathbb {R})^+ \times z_0$
.
$G(\mathbb {R})^+ \times z_0$
.
3.2 The associated vector bundles
Since
![]() $z_0$
is preserved by K, we have an orthogonal K-representation
$z_0$
is preserved by K, we have an orthogonal K-representation

where we will usually simply write
![]() $kw$
instead of
$kw$
instead of
![]() ${k\big|{}_{z_0} }w$
. We can consider the associated vector bundle
${k\big|{}_{z_0} }w$
. We can consider the associated vector bundle
![]() $P \times _K z_0$
which is the quotient of
$P \times _K z_0$
which is the quotient of
![]() $P \times z_0$
by K, where K acts by sending
$P \times z_0$
by K, where K acts by sending
![]() $(p,w)$
to
$(p,w)$
to
![]() $ (R_k(p), \rho (k)^{-1}w)$
. Hence, an element
$ (R_k(p), \rho (k)^{-1}w)$
. Hence, an element
![]() $[p,w]$
of
$[p,w]$
of
![]() $P \times _K z_0$
is an equivalence class where the equivalence relation identifies
$P \times _K z_0$
is an equivalence class where the equivalence relation identifies
![]() $(p,w)$
with
$(p,w)$
with
![]() $(R_k(p), \rho (k)^{-1}w)$
. This is a vector bundle over
$(R_k(p), \rho (k)^{-1}w)$
. This is a vector bundle over
![]() $P/K$
with projection map sending
$P/K$
with projection map sending
![]() $[p,w]$
to
$[p,w]$
to
![]() $\pi (p)$
. Let
$\pi (p)$
. Let
![]() $\Omega ^i(P/K,P \times _Kz_0)$
be the space of i-forms valued in
$\Omega ^i(P/K,P \times _Kz_0)$
be the space of i-forms valued in
![]() $P \times _Kz_0$
, when i is zero it is the space of smooth sections of the associated bundle.
$P \times _Kz_0$
, when i is zero it is the space of smooth sections of the associated bundle.
In the two cases of interest to us, we define

Note that in both cases, P admits a left action of
![]() $G(\mathbb {R})^+$
and that the associated vector bundles are
$G(\mathbb {R})^+$
and that the associated vector bundles are
![]() $G(\mathbb {R})^+$
-equivariant. Moreover, it is a Euclidean bundle, equipped with the inner product
$G(\mathbb {R})^+$
-equivariant. Moreover, it is a Euclidean bundle, equipped with the inner product
on the fiber. Let
![]() $ \Omega ^i(P,z_0)$
be the space of
$ \Omega ^i(P,z_0)$
be the space of
![]() $z_0$
-valued differential i-forms on P. A differential form
$z_0$
-valued differential i-forms on P. A differential form
![]() $\alpha $
in
$\alpha $
in
![]() $\Omega ^i(P,z_0)$
is said to be horizontal if
$\Omega ^i(P,z_0)$
is said to be horizontal if
![]() $\iota _X\alpha $
vanishes for all vertical vector fields X. There is a left action of K on a differential form
$\iota _X\alpha $
vanishes for all vertical vector fields X. There is a left action of K on a differential form
![]() $\alpha $
in
$\alpha $
in
![]() $\Omega ^i(P,z_0)$
defined by
$\Omega ^i(P,z_0)$
defined by
and
![]() $\alpha $
is K-invariant if it satisfies
$\alpha $
is K-invariant if it satisfies
![]() $k\cdot \alpha = \alpha $
for any k in
$k\cdot \alpha = \alpha $
for any k in
![]() $K,$
i.e., we have
$K,$
i.e., we have
![]() $R_k^\ast \alpha = \rho (k^{-1}) \alpha $
. We write
$R_k^\ast \alpha = \rho (k^{-1}) \alpha $
. We write
![]() $\Omega ^i(P, z_0)^K$
for the space of K-invariant
$\Omega ^i(P, z_0)^K$
for the space of K-invariant
![]() $z_0$
-valued forms on P. Finally, a form that is horizontal and K-invariant is called a basic form and the space of such forms is denoted by
$z_0$
-valued forms on P. Finally, a form that is horizontal and K-invariant is called a basic form and the space of such forms is denoted by
![]() $\Omega ^i(P,z_0)_{\mathrm{bas}}$
.
$\Omega ^i(P,z_0)_{\mathrm{bas}}$
.
Let
![]() $X_1, \dots , X_N$
be tangent vectors of
$X_1, \dots , X_N$
be tangent vectors of
![]() $P/K$
at
$P/K$
at
![]() $\pi (p),$
and let
$\pi (p),$
and let
![]() $\widetilde {X}_i$
be tangent vectors of P at p that satisfy
$\widetilde {X}_i$
be tangent vectors of P at p that satisfy
![]() $d_p\pi (\widetilde {X}_i)=X_i$
. There is a map
$d_p\pi (\widetilde {X}_i)=X_i$
. There is a map
 $$ \begin{align} \Omega^i(P,z_0)_{\mathrm{bas}} & \longrightarrow \Omega^i(P/K,P \times_K z_0) \nonumber \\ \alpha & \longmapsto \omega_\alpha \end{align} $$
$$ \begin{align} \Omega^i(P,z_0)_{\mathrm{bas}} & \longrightarrow \Omega^i(P/K,P \times_K z_0) \nonumber \\ \alpha & \longmapsto \omega_\alpha \end{align} $$
defined by
Proposition 3.1 The map is well-defined and yields an isomorphism between
![]() $\Omega ^i(P/K,P \times _K z_0)$
and
$\Omega ^i(P/K,P \times _K z_0)$
and
![]() $\Omega ^i(P,z_0)_{\mathrm{bas}}$
. In particular, if
$\Omega ^i(P,z_0)_{\mathrm{bas}}$
. In particular, if
![]() $z_0$
is one-dimensional, then
$z_0$
is one-dimensional, then
![]() $\Omega ^i(P/K)$
is isomorphic to
$\Omega ^i(P/K)$
is isomorphic to
![]() $\Omega ^i(P)_{\mathrm{bas}}$
.
$\Omega ^i(P)_{\mathrm{bas}}$
.
Proof In the case where i is zero, the horizontally condition is vacuous and the isomorphism simply identifies
![]() $\Omega ^0(P/K,P \times _K z_0)$
with
$\Omega ^0(P/K,P \times _K z_0)$
with
![]() $\Omega ^0(P,z_0)^K$
. We have a map
$\Omega ^0(P,z_0)^K$
. We have a map

which is well defined since
Conversely, every smooth section s in
![]() $\Omega ^0(P/K,P \times _K z_0)$
is given by
$\Omega ^0(P/K,P \times _K z_0)$
is given by
for some smooth function
![]() $f_s$
in
$f_s$
in
![]() $\Omega ^0(P,z_0)^K$
. The map sending s to
$\Omega ^0(P,z_0)^K$
. The map sending s to
![]() $f_s$
is inverse to the previous one. The proof is similar for positive i.
$f_s$
is inverse to the previous one. The proof is similar for positive i.
3.3 Covariant derivatives
A covariant derivative on the vector bundle
![]() $P \times _K z_0$
is a differential operator
$P \times _K z_0$
is a differential operator
such that for every smooth function f in
![]() $C^\infty (P/K),$
we have
$C^\infty (P/K),$
we have
The inner product on
![]() $P \times _Kz_0$
defines a pairing
$P \times _Kz_0$
defines a pairing
 $$ \begin{align} \Omega^i(P/K,P \times_K z_0) \times \Omega^j(P/K,P \times_K z_0) & \longrightarrow \Omega^{i+j}(P/K) \nonumber \\ ( \omega_1 \otimes s_1 , \omega_2 \otimes s_2 ) & \longmapsto \langle \omega_1 \otimes s_1 , \omega_2 \otimes s_2 \rangle = \omega_1 \wedge \omega_2 \langle s_1,s_2 \rangle, \end{align} $$
$$ \begin{align} \Omega^i(P/K,P \times_K z_0) \times \Omega^j(P/K,P \times_K z_0) & \longrightarrow \Omega^{i+j}(P/K) \nonumber \\ ( \omega_1 \otimes s_1 , \omega_2 \otimes s_2 ) & \longmapsto \langle \omega_1 \otimes s_1 , \omega_2 \otimes s_2 \rangle = \omega_1 \wedge \omega_2 \langle s_1,s_2 \rangle, \end{align} $$
and we say that the derivative is compatible with the metric if
for any two sections
![]() $s_1$
and
$s_1$
and
![]() $s_2$
in
$s_2$
in
![]() $\Omega ^0(P/K,P\times _Kz_0)$
. There is a covariant derivative that is induced by a principal connection
$\Omega ^0(P/K,P\times _Kz_0)$
. There is a covariant derivative that is induced by a principal connection
![]() $\theta _P$
in
$\theta _P$
in
![]() $\Omega ^1(P) \otimes \mathfrak {k}$
as follows. The derivative of the representation gives a map
$\Omega ^1(P) \otimes \mathfrak {k}$
as follows. The derivative of the representation gives a map
which we also denote by
![]() $\rho $
by abuse of notation. Note that for the representation (3.11), this is simply the map
$\rho $
by abuse of notation. Note that for the representation (3.11), this is simply the map
 $$ \begin{align} \rho \colon \mathfrak{k} & \longrightarrow \mathfrak{so}(z_0) \nonumber \\ X & \longmapsto {{X}\big|{}_{z_0} }, \end{align} $$
$$ \begin{align} \rho \colon \mathfrak{k} & \longrightarrow \mathfrak{so}(z_0) \nonumber \\ X & \longmapsto {{X}\big|{}_{z_0} }, \end{align} $$
since
![]() $\mathfrak {k}$
splits as
$\mathfrak {k}$
splits as
![]() $\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$
. Composing the principal connection with
$\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$
. Composing the principal connection with
![]() $\rho $
defines an element
$\rho $
defines an element
In particular, if s is a section of
![]() $P \times _K z_0$
, then we can identify it with a K-invariant smooth map
$P \times _K z_0$
, then we can identify it with a K-invariant smooth map
![]() $f_s$
in
$f_s$
in
![]() $\Omega ^0(P, z_0)^K$
. Since
$\Omega ^0(P, z_0)^K$
. Since
![]() $\rho (\theta _P)$
is a
$\rho (\theta _P)$
is a
![]() $\mathfrak {so}(z_0)$
-valued form and
$\mathfrak {so}(z_0)$
-valued form and
![]() $\mathfrak {so}(z_0)$
is a subspace of
$\mathfrak {so}(z_0)$
is a subspace of
![]() $\operatorname {End}(z_0),$
we can define
$\operatorname {End}(z_0),$
we can define
Lemma 3.2 The form
![]() $df_s+\rho (\theta _P) \cdot f_s$
is basic, hence gives a
$df_s+\rho (\theta _P) \cdot f_s$
is basic, hence gives a
![]() $P \times _K z_0$
-valued form on
$P \times _K z_0$
-valued form on
![]() $P/K$
. Thus,
$P/K$
. Thus,
![]() $d+\rho (\theta _P)$
defines a covariant derivative on
$d+\rho (\theta _P)$
defines a covariant derivative on
![]() $P \times _K z_0$
. Moreover, it is compatible with the metric.
$P \times _K z_0$
. Moreover, it is compatible with the metric.
Proof See [Reference Berline, Getzler and Vergne1, p. 24]. For the compatibility with the metric, it follows from the fact that the connection
![]() $\rho (\theta _P)$
is valued in
$\rho (\theta _P)$
is valued in
![]() $\mathfrak {so}(z_0)$
that
$\mathfrak {so}(z_0)$
that
Hence, if we denote by
![]() $\nabla _P$
is the covariant derivative defined by
$\nabla _P$
is the covariant derivative defined by
![]() $d+\rho (\theta _P),$
then
$d+\rho (\theta _P),$
then
Let us denote by
![]() $\nabla _P$
the covariant derivative
$\nabla _P$
the covariant derivative
![]() $d+\rho (\theta _P)$
. It can be extended to a map
$d+\rho (\theta _P)$
. It can be extended to a map
by setting
where
We define the curvature
![]() $R_P$
in
$R_P$
in
![]() $\Omega ^2(P,\mathfrak {k})$
by
$\Omega ^2(P,\mathfrak {k})$
by
for two vector fields X and Y on P. It is basic by [Reference Berline, Getzler and Vergne1, Proposition 1.13] and composing with
![]() $\rho $
gives an element
$\rho $
gives an element
so that we can view it as an element in
![]() $\Omega ^2(P/K,P \times _K \mathfrak {so}(z_0)),$
where K acts on
$\Omega ^2(P/K,P \times _K \mathfrak {so}(z_0)),$
where K acts on
![]() $\mathfrak {so}(z_0)$
by the
$\mathfrak {so}(z_0)$
by the
![]() $\operatorname {Ad}$
-representation. For a section s in
$\operatorname {Ad}$
-representation. For a section s in
![]() $\Omega ^0(P/K,P \times _K z_0)$
, we have [Reference Berline, Getzler and Vergne1, Proposition 1.15]
$\Omega ^0(P/K,P \times _K z_0)$
, we have [Reference Berline, Getzler and Vergne1, Proposition 1.15]
From now on, we denote by
![]() $\nabla $
and
$\nabla $
and
![]() $\widetilde {\nabla }$
the covariant derivatives on E and
$\widetilde {\nabla }$
the covariant derivatives on E and
![]() $\widetilde {E}$
associated with
$\widetilde {E}$
associated with
![]() $\theta $
and
$\theta $
and
![]() $\widetilde {\theta }$
defined in (3.7) and (3.10). Let R and
$\widetilde {\theta }$
defined in (3.7) and (3.10). Let R and
![]() $\widetilde {R}$
be their respective curvatures.
$\widetilde {R}$
be their respective curvatures.
3.4 Pullback of bundles
The pullback of E by the projection map gives a canonical bundle
over E. We have the following diagram:

The projection induces a pullback of the sections
We can also pullback the covariant derivative
![]() $\nabla $
to a covariant derivative
$\nabla $
to a covariant derivative
on
![]() $\pi ^\ast E$
. It is characterized by the property
$\pi ^\ast E$
. It is characterized by the property
Proposition 3.3 The bundles
![]() $\widetilde {E}$
and
$\widetilde {E}$
and
![]() $\pi ^\ast E$
are isomorphic, and this isomorphism identifies
$\pi ^\ast E$
are isomorphic, and this isomorphism identifies
![]() $\widetilde {\nabla }$
and
$\widetilde {\nabla }$
and
![]() $\pi ^\ast \nabla $
.
$\pi ^\ast \nabla $
.
Proof By definition,
![]() $([g_1,w_1],[g_2,w_2])$
are elements of
$([g_1,w_1],[g_2,w_2])$
are elements of
![]() $ \pi ^\ast E$
if and only if
$ \pi ^\ast E$
if and only if
![]() $g^{-1}_1g_2$
is in K. We have a
$g^{-1}_1g_2$
is in K. We have a
![]() $G(\mathbb {R})^+$
-equivariant morphism
$G(\mathbb {R})^+$
-equivariant morphism
 $$ \begin{align} \pi^\ast E & \longrightarrow \widetilde{E} \nonumber \\ ([g_1,w_1],[g_2,w_2]) & \longrightarrow [(g_1,g_1^{-1}g_2w_2),w_1]. \end{align} $$
$$ \begin{align} \pi^\ast E & \longrightarrow \widetilde{E} \nonumber \\ ([g_1,w_1],[g_2,w_2]) & \longrightarrow [(g_1,g_1^{-1}g_2w_2),w_1]. \end{align} $$
This map is well defined and has as inverse
 $$ \begin{align} \widetilde{E} & \longrightarrow \pi^\ast E \nonumber \\ [(g,w_1),w_2] & \longrightarrow ([g,w_2],[g,w_1]). \end{align} $$
$$ \begin{align} \widetilde{E} & \longrightarrow \pi^\ast E \nonumber \\ [(g,w_1),w_2] & \longrightarrow ([g,w_2],[g,w_1]). \end{align} $$
The second statement follows from the fact that
![]() $\widetilde {\theta }$
is
$\widetilde {\theta }$
is
![]() $\pi ^\ast \theta $
.
$\pi ^\ast \theta $
.
3.5 A few operations on the vector bundles
We extend the K-representation
![]() $z_0$
to
$z_0$
to
![]() $\bigwedge ^j z_0$
by
$\bigwedge ^j z_0$
by
We consider the bundles
![]() $P \times _K \wedge ^j z_0$
and
$P \times _K \wedge ^j z_0$
and
![]() $ P \times _K \wedge z_0$
over
$ P \times _K \wedge z_0$
over
![]() $P/K$
, where
$P/K$
, where
![]() $\bigwedge z_0$
is defined as
$\bigwedge z_0$
is defined as
![]() $ \bigoplus _i \bigwedge ^iz_0$
. Denote the space of differential forms valued in
$ \bigoplus _i \bigwedge ^iz_0$
. Denote the space of differential forms valued in
![]() $P \times _K \wedge ^j z_0$
by
$P \times _K \wedge ^j z_0$
by
The total space of differential forms
is an (associative) bigraded
![]() $C^\infty (P/K)$
-algebra, where the product is defined by
$C^\infty (P/K)$
-algebra, where the product is defined by

This algebra structure allows us to define an exponential map by

where
![]() $\omega ^k$
is the k-fold wedge product
$\omega ^k$
is the k-fold wedge product
![]() $\omega \wedge \cdots \wedge \omega $
.
$\omega \wedge \cdots \wedge \omega $
.
Remark 3.1 Suppose that
![]() $\omega $
and
$\omega $
and
![]() $\eta $
commute. Then the binomial formula
$\eta $
commute. Then the binomial formula
 $$ \begin{align} (\omega+\eta)^k=\sum_{l=0}^k \binom{k}{l}\omega^l\eta^{k-l} \end{align} $$
$$ \begin{align} (\omega+\eta)^k=\sum_{l=0}^k \binom{k}{l}\omega^l\eta^{k-l} \end{align} $$
holds and one can show that
![]() $\exp (\omega +\eta )=\exp (\omega )+\exp (\eta )$
in the same way as for the real exponential map. In particular, the diagonal subalgebra
$\exp (\omega +\eta )=\exp (\omega )+\exp (\eta )$
in the same way as for the real exponential map. In particular, the diagonal subalgebra
![]() $\bigoplus \Omega _P^{i,i}$
is a commutative, since for two forms
$\bigoplus \Omega _P^{i,i}$
is a commutative, since for two forms
![]() $\omega $
and
$\omega $
and
![]() $\eta $
in
$\eta $
in
![]() $\Omega _P$
, we have
$\Omega _P$
, we have
and similarly for two sections s and t in
![]() $\Omega ^0(P/K,P \times _K z_0)$
.
$\Omega ^0(P/K,P \times _K z_0)$
.
The inner product
![]() $\langle - , - \rangle $
on
$\langle - , - \rangle $
on
![]() $z_0$
can be extended to an inner product on
$z_0$
can be extended to an inner product on
![]() $\bigwedge z_0$
by
$\bigwedge z_0$
by

If
![]() $e_1, \dots , e_q$
is an orthonormal basis of
$e_1, \dots , e_q$
is an orthonormal basis of
![]() $z_0$
, then the set
$z_0$
, then the set
is an orthonormal basis of
![]() $\bigwedge z_0$
. We define the Berezin integral
$\bigwedge z_0$
. We define the Berezin integral
![]() $\int ^B$
to be the orthogonal projection onto the top dimensional component, that is the map
$\int ^B$
to be the orthogonal projection onto the top dimensional component, that is the map
 $$ \begin{align} \int^B \colon \bigwedge z_0& \longrightarrow \mathbb{R} \nonumber \\ w & \longmapsto \langle w \; , \;e_1\wedge \cdots \wedge e_q \rangle. \end{align} $$
$$ \begin{align} \int^B \colon \bigwedge z_0& \longrightarrow \mathbb{R} \nonumber \\ w & \longmapsto \langle w \; , \;e_1\wedge \cdots \wedge e_q \rangle. \end{align} $$
The Berezin integral can then be extended to
 $$ \begin{align} \int^B \colon \Omega(P/K,P\times_K \wedge z_0) & \longrightarrow \Omega(P/K) \nonumber \\ \omega \otimes s & \longmapsto \omega \int^B s, \end{align} $$
$$ \begin{align} \int^B \colon \Omega(P/K,P\times_K \wedge z_0) & \longrightarrow \Omega(P/K) \nonumber \\ \omega \otimes s & \longmapsto \omega \int^B s, \end{align} $$
where
![]() $\int ^B s$
in
$\int ^B s$
in
![]() $C^\infty (P/K)$
is the composition of the section with the Berezinian in every fiber. Let
$C^\infty (P/K)$
is the composition of the section with the Berezinian in every fiber. Let
![]() $s_1, \dots , s_q$
be a local orthonormal frame of
$s_1, \dots , s_q$
be a local orthonormal frame of
![]() $P \times _K z_0$
. Then
$P \times _K z_0$
. Then
![]() $s_1 \wedge \cdots \wedge s_q$
is in
$s_1 \wedge \cdots \wedge s_q$
is in
![]() $\Omega ^0(P/K,\wedge ^q P \times _K z_0)$
and defines a global section. Hence, for
$\Omega ^0(P/K,\wedge ^q P \times _K z_0)$
and defines a global section. Hence, for
![]() $\alpha $
in
$\alpha $
in
![]() $\Omega (P/K,P\times _K \wedge z_0),$
we have
$\Omega (P/K,P\times _K \wedge z_0),$
we have
Finally, for every section s in
![]() $\Omega ^{0,1}$
, we can define the contraction
$\Omega ^{0,1}$
, we can define the contraction
 $$ \begin{align} i(s) \colon \Omega_P^{i,j} & \longrightarrow \Omega_P^{i,j-1} \nonumber \\ \omega \otimes s_1 \wedge \cdots \wedge s_j & \longmapsto \sum_{k=1}^j (-1)^{i+k-1}\langle s,s_k \rangle \omega \otimes s_1\wedge \cdots \wedge \widehat{s_k} \wedge \cdots \wedge s_j, \end{align} $$
$$ \begin{align} i(s) \colon \Omega_P^{i,j} & \longrightarrow \Omega_P^{i,j-1} \nonumber \\ \omega \otimes s_1 \wedge \cdots \wedge s_j & \longmapsto \sum_{k=1}^j (-1)^{i+k-1}\langle s,s_k \rangle \omega \otimes s_1\wedge \cdots \wedge \widehat{s_k} \wedge \cdots \wedge s_j, \end{align} $$
and extended by linearity, where the symbol
![]() $ \, \widehat {\cdot } \,$
means that we remove it from the product. Note that when j is zero, then
$ \, \widehat {\cdot } \,$
means that we remove it from the product. Note that when j is zero, then
![]() $i(s)$
is defined to be zero. The contraction
$i(s)$
is defined to be zero. The contraction
![]() $i(s)$
defines a derivation on
$i(s)$
defines a derivation on
![]() $\oplus \widetilde {\Omega }^{i,j}$
that satisfies
$\oplus \widetilde {\Omega }^{i,j}$
that satisfies
for
![]() $\alpha $
in
$\alpha $
in
![]() $\widetilde {\Omega }^{i,j}$
and
$\widetilde {\Omega }^{i,j}$
and
![]() $\alpha '$
in
$\alpha '$
in
![]() $\widetilde {\Omega }^{k,l}$
.
$\widetilde {\Omega }^{k,l}$
.
3.6 Thom forms
We denote by E the bundle
![]() $G(\mathbb {R})^+\times _K z_0$
. On the fibers of the bundle, we have the inner product given by
$G(\mathbb {R})^+\times _K z_0$
. On the fibers of the bundle, we have the inner product given by
![]() . Let v be arbitrary vector in L and
. Let v be arbitrary vector in L and
![]() $\Gamma _v$
its stabilizer. Since the bundle is
$\Gamma _v$
its stabilizer. Since the bundle is
![]() $G(\mathbb {R})^+$
-equivariant, we have a bundle
$G(\mathbb {R})^+$
-equivariant, we have a bundle
and let
![]() $\operatorname {D}(\Gamma _v \backslash E)$
be the closed disk bundle. If we have a closed
$\operatorname {D}(\Gamma _v \backslash E)$
be the closed disk bundle. If we have a closed
![]() $(q+i)$
-form on
$(q+i)$
-form on
![]() $\Gamma _v \backslash E$
whose support is contained in
$\Gamma _v \backslash E$
whose support is contained in
![]() $\operatorname {D}(\Gamma _v \backslash E)$
, then it has compact support in the fiber and represents a class in
$\operatorname {D}(\Gamma _v \backslash E)$
, then it has compact support in the fiber and represents a class in
![]() $H^{q+i}(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$
. The cohomology group
$H^{q+i}(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$
. The cohomology group
![]() $H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$
is equal to the cohomology group
$H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$
is equal to the cohomology group
![]() $H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$
that we used in the introduction, where
$H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$
that we used in the introduction, where
![]() $E_0$
is the zero section. Fiber integration induces an isomorphism on the level of cohomology
$E_0$
is the zero section. Fiber integration induces an isomorphism on the level of cohomology
 $$ \begin{align} \operatorname{Th} \colon H^{q+i}(\Gamma_v \backslash E,\Gamma_v \backslash E-\operatorname{D}(\Gamma_v \backslash E)) & \longrightarrow H^i(\Gamma_v \backslash \mathbb{D}^+) \nonumber \\ [\omega] & \longmapsto \int_{\mathrm{fiber}} \omega \end{align} $$
$$ \begin{align} \operatorname{Th} \colon H^{q+i}(\Gamma_v \backslash E,\Gamma_v \backslash E-\operatorname{D}(\Gamma_v \backslash E)) & \longrightarrow H^i(\Gamma_v \backslash \mathbb{D}^+) \nonumber \\ [\omega] & \longmapsto \int_{\mathrm{fiber}} \omega \end{align} $$
known as the Thom isomorphism [Reference Bott and Tu2, Theorem 6.17]. When i is zero, then
![]() $H^i(\Gamma _v \backslash \mathbb {D}^+)$
is
$H^i(\Gamma _v \backslash \mathbb {D}^+)$
is
![]() $\mathbb {R}$
and we call the preimage of
$\mathbb {R}$
and we call the preimage of
![]() $1$
$1$
the Thom class. Any differential form representating this class is called a Thom form, in particular, every closed q-form on
![]() $\Gamma _v \backslash E$
that has compact support in every fiber and whose integral along every fiber is
$\Gamma _v \backslash E$
that has compact support in every fiber and whose integral along every fiber is
![]() $1$
is a Thom form. One can also view the Thom class as the Poincaré dual class of the zero section
$1$
is a Thom form. One can also view the Thom class as the Poincaré dual class of the zero section
![]() $E_0$
in E, in the same sense as for (2.24).
$E_0$
in E, in the same sense as for (2.24).
Let
![]() $\omega $
in
$\omega $
in
![]() $\Omega ^j(E)$
be a form on the bundle, and let
$\Omega ^j(E)$
be a form on the bundle, and let
![]() $\omega _z$
be its restriction to a fiber
$\omega _z$
be its restriction to a fiber
![]() $E_z=\pi ^{-1}(z)$
for some z in
$E_z=\pi ^{-1}(z)$
for some z in
![]() $\mathbb {D}^+$
. After identifying
$\mathbb {D}^+$
. After identifying
![]() $z_0$
with
$z_0$
with
![]() $\mathbb {R}^q$
, we see
$\mathbb {R}^q$
, we see
![]() $\omega _z$
as an element of
$\omega _z$
as an element of
![]() $C^\infty (\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $
. We say that
$C^\infty (\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $
. We say that
![]() $\omega $
is rapidly decreasing in the fiber, if
$\omega $
is rapidly decreasing in the fiber, if
![]() $\omega _z$
lies in
$\omega _z$
lies in
![]() $\mathscr {S}(\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $
for every z in
$\mathscr {S}(\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $
for every z in
![]() $\mathbb {D}^+$
. We write
$\mathbb {D}^+$
. We write
![]() $\Omega ^j_{\textrm {rd}}(E)$
for the space of such forms.
$\Omega ^j_{\textrm {rd}}(E)$
for the space of such forms.
Let
![]() $\Omega ^\bullet _{\textrm {rd}}(\Gamma _v \backslash E)$
be the complex of rapidly decreasing forms in the fiber. It is isomorphic to the complex
$\Omega ^\bullet _{\textrm {rd}}(\Gamma _v \backslash E)$
be the complex of rapidly decreasing forms in the fiber. It is isomorphic to the complex
![]() $\Omega ^\bullet _{\textrm {rd}}(E)^{\Gamma _v}$
of rapidly decreasing
$\Omega ^\bullet _{\textrm {rd}}(E)^{\Gamma _v}$
of rapidly decreasing
![]() $\Gamma _v$
-invariant forms on E. Let
$\Gamma _v$
-invariant forms on E. Let
![]() $H_{\textrm {rd}}(\Gamma _v \backslash E)$
the cohomology of this complex. The map
$H_{\textrm {rd}}(\Gamma _v \backslash E)$
the cohomology of this complex. The map
 $$ \begin{align} h \colon \Gamma_v \backslash E & \longrightarrow \Gamma_v \backslash E \nonumber \\ w & \longrightarrow \frac{w}{\sqrt{1-\lVert {w} \rVert^2}} \end{align} $$
$$ \begin{align} h \colon \Gamma_v \backslash E & \longrightarrow \Gamma_v \backslash E \nonumber \\ w & \longrightarrow \frac{w}{\sqrt{1-\lVert {w} \rVert^2}} \end{align} $$
is a diffeomorphism from the open disk bundle
![]() $\operatorname {D}(\Gamma _v \backslash E)^\circ $
onto
$\operatorname {D}(\Gamma _v \backslash E)^\circ $
onto
![]() $\Gamma _v \backslash E$
. It induces an isomorphism by pullback
$\Gamma _v \backslash E$
. It induces an isomorphism by pullback
which commutes with the fiber integration. Hence, we have the following version of the Thom isomorphism:
The construction of Mathai and Quillen produces a Thom form
which is
![]() $G(\mathbb {R})^+$
-invariant (hence,
$G(\mathbb {R})^+$
-invariant (hence,
![]() $\Gamma _v$
-invariant) and closed. We will recall their construction in the next section.
$\Gamma _v$
-invariant) and closed. We will recall their construction in the next section.
3.7 The Mathai–Quillen construction
As earlier, let
![]() $\widetilde {E}$
be the bundle
$\widetilde {E}$
be the bundle
![]() $(G(\mathbb {R})^+ \times z_0) \times _K z_0$
. Let
$(G(\mathbb {R})^+ \times z_0) \times _K z_0$
. Let
![]() $ \wedge ^j \tilde {E} $
be the bundle
$ \wedge ^j \tilde {E} $
be the bundle
![]() $(G(\mathbb {R})^+ \times z_0) \times _K \wedge ^j z_0$
and
$(G(\mathbb {R})^+ \times z_0) \times _K \wedge ^j z_0$
and

First, consider the tautological section
![]() $\mathbf{s}$
of
$\mathbf{s}$
of
![]() $\widetilde {E}$
defined by
$\widetilde {E}$
defined by
This gives a canonical element
![]() $\mathbf{s}$
of
$\mathbf{s}$
of
![]() $\widetilde {\Omega }^{0,1}$
. Composing with the norm induced from the inner product, we get an element
$\widetilde {\Omega }^{0,1}$
. Composing with the norm induced from the inner product, we get an element
![]() $\lVert \mathbf{s} \rVert ^2$
in
$\lVert \mathbf{s} \rVert ^2$
in
![]() $\widetilde {\Omega }^{0,0}$
.
$\widetilde {\Omega }^{0,0}$
.
The representation
![]() $\rho $
on
$\rho $
on
![]() $z_0$
induces a representation on
$z_0$
induces a representation on
![]() $\wedge ^iz_0$
that we also denote by
$\wedge ^iz_0$
that we also denote by
![]() $\rho $
. The derivative at the identity gives a map
$\rho $
. The derivative at the identity gives a map
The connection form
![]() $\rho (\widetilde {\theta })$
in
$\rho (\widetilde {\theta })$
in
![]() $\Omega ^1(G(\mathbb {R})^+ \times z_0,\wedge ^j z_0)$
defines a covariant derivative
$\Omega ^1(G(\mathbb {R})^+ \times z_0,\wedge ^j z_0)$
defines a covariant derivative
on
![]() $\wedge ^j \widetilde {E}$
. We can extend it to a map
$\wedge ^j \widetilde {E}$
. We can extend it to a map
by setting
as in (3.30). The connection on
![]() $\widetilde {\Omega }^{i,j}$
is compatible with the metric. Finally, the covariant derivative
$\widetilde {\Omega }^{i,j}$
is compatible with the metric. Finally, the covariant derivative
![]() $\widetilde {\nabla }$
defines a derivation on
$\widetilde {\nabla }$
defines a derivation on
![]() $\oplus \widetilde {\Omega }^{i,j}$
that satisfies
$\oplus \widetilde {\Omega }^{i,j}$
that satisfies
for any
![]() $\alpha $
in
$\alpha $
in
![]() $\widetilde {\Omega }^{i,j}$
and
$\widetilde {\Omega }^{i,j}$
and
![]() $\alpha '$
in
$\alpha '$
in
![]() $\widetilde {\Omega }^{k,l}$
.
$\widetilde {\Omega }^{k,l}$
.
Taking the derivative of the tautological section gives an element
Let
![]() $\mathfrak {so}(\widetilde {E})$
denote the bundle
$\mathfrak {so}(\widetilde {E})$
denote the bundle
![]() $(G(\mathbb {R})^+ \times z_0) \times _K \mathfrak {so}(z_0)$
and consider the curvature
$(G(\mathbb {R})^+ \times z_0) \times _K \mathfrak {so}(z_0)$
and consider the curvature
![]() $\rho (\widetilde {R})$
in
$\rho (\widetilde {R})$
in
![]() $\Omega ^2(\widetilde {E}, \mathfrak {so}(\widetilde {E}))$
. We have an isomorphism
$\Omega ^2(\widetilde {E}, \mathfrak {so}(\widetilde {E}))$
. We have an isomorphism
 $$ \begin{align} {{T^{-1}}\big|{}_{z_0} } \colon \mathfrak{so}(z_0) & \longrightarrow \wedge^2 z_0 \nonumber \\ A & \longmapsto \sum_{i<j}\langle Ae_i,e_j\rangle e_i \wedge e_j. \end{align} $$
$$ \begin{align} {{T^{-1}}\big|{}_{z_0} } \colon \mathfrak{so}(z_0) & \longrightarrow \wedge^2 z_0 \nonumber \\ A & \longmapsto \sum_{i<j}\langle Ae_i,e_j\rangle e_i \wedge e_j. \end{align} $$
The inverse sends
![]() $v \wedge w$
to the endomorphism
$v \wedge w$
to the endomorphism
![]() $ u \mapsto \langle v,u \rangle w-\langle w,u \rangle v$
, and is the isomorphism from (2.11) restricted to
$ u \mapsto \langle v,u \rangle w-\langle w,u \rangle v$
, and is the isomorphism from (2.11) restricted to
![]() $z_0$
. Note that we have
$z_0$
. Note that we have
Using this isomorphism, we can also identify
![]() $\mathfrak {so}(\widetilde {E})$
and
$\mathfrak {so}(\widetilde {E})$
and
![]() $\wedge ^2 \widetilde {E}$
so that we can view the curvature as an element
$\wedge ^2 \widetilde {E}$
so that we can view the curvature as an element
Lemma 3.4 The form
![]() lying in
lying in
![]() $\widetilde {\Omega }^{0,0} \oplus \widetilde {\Omega }^{1,1} \oplus \widetilde {\Omega }^{2,2}$
is annihilated by
$\widetilde {\Omega }^{0,0} \oplus \widetilde {\Omega }^{1,1} \oplus \widetilde {\Omega }^{2,2}$
is annihilated by
![]() $\widetilde {\nabla }+ 2 \sqrt {\pi } i(\mathbf{s})$
. Moreover
$\widetilde {\nabla }+ 2 \sqrt {\pi } i(\mathbf{s})$
. Moreover
for every form
![]() $\alpha $
in
$\alpha $
in
![]() $\widetilde {\Omega }^{i,j}$
. Hence,
$\widetilde {\Omega }^{i,j}$
. Hence,
![]() $\int ^B exp(-\omega )$
is a closed form.
$\int ^B exp(-\omega )$
is a closed form.
Proof We have
 $$ \begin{align} & \left (\widetilde{\nabla}+ 2 \sqrt{\pi} i(\mathbf{s}) \right ) \left ( 2 \pi \lVert \mathbf{s} \rVert^2+2 \sqrt{\pi}\widetilde{\nabla} \mathbf{s}-\rho(\widetilde{R}) \right ) \\ & = 2 \pi \widetilde{\nabla} \lVert \mathbf{s} \rVert^2 + 4\pi^{\frac{3}{2}}i(\mathbf{s}) \lVert \mathbf{s} \rVert^2 + 2 \sqrt{\pi} \widetilde{\nabla}^2 \mathbf{s}+4 \pi i(x) \widetilde{\nabla} \mathbf{s}-\widetilde{\nabla} \rho(\widetilde{R})-2 \sqrt{\pi} i(\mathbf{s}) \rho(\widetilde{R}). \nonumber \end{align} $$
$$ \begin{align} & \left (\widetilde{\nabla}+ 2 \sqrt{\pi} i(\mathbf{s}) \right ) \left ( 2 \pi \lVert \mathbf{s} \rVert^2+2 \sqrt{\pi}\widetilde{\nabla} \mathbf{s}-\rho(\widetilde{R}) \right ) \\ & = 2 \pi \widetilde{\nabla} \lVert \mathbf{s} \rVert^2 + 4\pi^{\frac{3}{2}}i(\mathbf{s}) \lVert \mathbf{s} \rVert^2 + 2 \sqrt{\pi} \widetilde{\nabla}^2 \mathbf{s}+4 \pi i(x) \widetilde{\nabla} \mathbf{s}-\widetilde{\nabla} \rho(\widetilde{R})-2 \sqrt{\pi} i(\mathbf{s}) \rho(\widetilde{R}). \nonumber \end{align} $$
It vanishes, because we have the following:
-
∙
 $i(\mathbf{s}) \lVert \mathbf{s} \rVert ^2=0$
since
$i(\mathbf{s}) \lVert \mathbf{s} \rVert ^2=0$
since
 $\lVert \mathbf{s} \rVert $
is in
$\lVert \mathbf{s} \rVert $
is in
 $\widetilde {\Omega }^{0,0}$
,
$\widetilde {\Omega }^{0,0}$
, -
∙
 $\widetilde {\nabla } \rho (\widetilde {R})=0$
by Bianchi’s identity,
$\widetilde {\nabla } \rho (\widetilde {R})=0$
by Bianchi’s identity, -
∙
 $\widetilde {\nabla }\lVert \mathbf{s} \rVert ^2= 2\langle \widetilde {\nabla }\mathbf{s},\mathbf{s} \rangle =-2 i(\mathbf{s}) \widetilde {\nabla }\mathbf{s} $
,
$\widetilde {\nabla }\lVert \mathbf{s} \rVert ^2= 2\langle \widetilde {\nabla }\mathbf{s},\mathbf{s} \rangle =-2 i(\mathbf{s}) \widetilde {\nabla }\mathbf{s} $
, -
∙
 $\widetilde {\nabla }^2\mathbf{s}=\rho (\widetilde {R})\mathbf{s} =i(\mathbf{s})\rho (\widetilde {R})$
.
$\widetilde {\nabla }^2\mathbf{s}=\rho (\widetilde {R})\mathbf{s} =i(\mathbf{s})\rho (\widetilde {R})$
.
For the last point, we used (3.73), where we view
![]() $\rho (\widetilde {R})$
as an element of
$\rho (\widetilde {R})$
as an element of
![]() $\Omega ^2(E,\mathfrak {so}(\widetilde {E}))$
, respectively of
$\Omega ^2(E,\mathfrak {so}(\widetilde {E}))$
, respectively of
![]() $\Omega ^2(E,\wedge ^2\widetilde {E})$
.
$\Omega ^2(E,\wedge ^2\widetilde {E})$
.
Let
![]() $s_1 \wedge \cdots \wedge s_q$
in
$s_1 \wedge \cdots \wedge s_q$
in
![]() $\Omega ^0(E,\wedge ^q \widetilde {E})$
be a global section, where
$\Omega ^0(E,\wedge ^q \widetilde {E})$
be a global section, where
![]() $s_1, \dots , s_q$
is a local orthonormal frame for
$s_1, \dots , s_q$
is a local orthonormal frame for
![]() $\widetilde {E}$
. Then, for any
$\widetilde {E}$
. Then, for any
![]() $\alpha $
in
$\alpha $
in
![]() $\widetilde {\Omega }^{i,j}$
, we have
$\widetilde {\Omega }^{i,j}$
, we have
This vanishes if j is different from q, hence we can assume
![]() $\alpha $
is in
$\alpha $
is in
![]() $\widetilde {\Omega }^{i,q}$
. If we write
$\widetilde {\Omega }^{i,q}$
. If we write
![]() $\alpha $
as
$\alpha $
as
![]() $\beta s_1 \wedge \cdots \wedge s_q$
for some
$\beta s_1 \wedge \cdots \wedge s_q$
for some
![]() $\beta $
in
$\beta $
in
![]() $\Omega ^i(E)$
, then
$\Omega ^i(E)$
, then
On the other hand, since the connection on
![]() $\widetilde {\Omega }^{i,q}$
is compatible with the metric, we have
$\widetilde {\Omega }^{i,q}$
is compatible with the metric, we have
Then we have
 $$ \begin{align} \int^B \widetilde{\nabla} \alpha & =\langle \widetilde{\nabla} \alpha, s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = \langle d\beta \otimes s_1 \wedge \cdots \wedge s_q + (-1)^i \beta \wedge \widetilde{\nabla}( s_1 \wedge \cdots \wedge s_q),s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = d \beta \nonumber \\ & = d \int^B \alpha. \end{align} $$
$$ \begin{align} \int^B \widetilde{\nabla} \alpha & =\langle \widetilde{\nabla} \alpha, s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = \langle d\beta \otimes s_1 \wedge \cdots \wedge s_q + (-1)^i \beta \wedge \widetilde{\nabla}( s_1 \wedge \cdots \wedge s_q),s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = d \beta \nonumber \\ & = d \int^B \alpha. \end{align} $$
Since
![]() $\widetilde {\nabla } + 2 \sqrt {\pi }i(\mathbf{s})$
is a derivation that annihilates
$\widetilde {\nabla } + 2 \sqrt {\pi }i(\mathbf{s})$
is a derivation that annihilates
![]() $\omega $
, we have
$\omega $
, we have
for positive k. Hence, it follows that
 $$ \begin{align} d \int^B \exp(-\omega) & = \int^B \widetilde{\nabla} \exp(-\omega) \nonumber \\ & = \int^B \left (\widetilde{\nabla}+2 \sqrt{\pi}i(\mathbf{s}) \right )\exp(-\omega) \nonumber \\ & =0.\\[-34pt]\nonumber \end{align} $$
$$ \begin{align} d \int^B \exp(-\omega) & = \int^B \widetilde{\nabla} \exp(-\omega) \nonumber \\ & = \int^B \left (\widetilde{\nabla}+2 \sqrt{\pi}i(\mathbf{s}) \right )\exp(-\omega) \nonumber \\ & =0.\\[-34pt]\nonumber \end{align} $$
In [Reference Mathai and Quillen10], Mathai and Quillen define the following form:
We call it the Mathai–Quillen form.
Proposition 3.5 The Mathai–Quillen form is a Thom form.
Proof From the previous lemma, it follows that the form is closed. It remains to show that its integral along the fibers is
![]() $1$
. The restriction of the form
$1$
. The restriction of the form
![]() $U_{MQ}$
along the fiber
$U_{MQ}$
along the fiber
![]() $\pi ^{-1}(eK)$
is given by
$\pi ^{-1}(eK)$
is given by
 $$ \begin{align} U_{MQ} & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} \int^B \exp(-2 \sqrt{\pi} d \mathbf{s}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} (-1)^q \int^B (dx_1 \otimes e_1) \wedge \cdots \wedge (dx_q \otimes e_q) \nonumber \\ & = 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} dx_1 \wedge \cdots \wedge dx_q, \end{align} $$
$$ \begin{align} U_{MQ} & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} \int^B \exp(-2 \sqrt{\pi} d \mathbf{s}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} (-1)^q \int^B (dx_1 \otimes e_1) \wedge \cdots \wedge (dx_q \otimes e_q) \nonumber \\ & = 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} dx_1 \wedge \cdots \wedge dx_q, \end{align} $$
and its integral over the fiber
![]() $\pi ^{-1}(eK)$
is equal to
$\pi ^{-1}(eK)$
is equal to
![]() $1$
.
$1$
.
4 Computation of the Mathai–Quillen form
4.1 The section
 $s_v$
$s_v$
Let
![]() $\textrm {pr}$
denote the orthogonal projection of
$\textrm {pr}$
denote the orthogonal projection of
![]() $V(\mathbb {R})$
on the plane
$V(\mathbb {R})$
on the plane
![]() $z_0$
. Consider the section
$z_0$
. Consider the section
 $$ \begin{align} s_v \colon \mathbb{D}^+ & \longrightarrow E \nonumber \\ z \; & \longmapsto [g_z,\textrm{pr}(g_z^{-1}v)], \end{align} $$
$$ \begin{align} s_v \colon \mathbb{D}^+ & \longrightarrow E \nonumber \\ z \; & \longmapsto [g_z,\textrm{pr}(g_z^{-1}v)], \end{align} $$
where
![]() $g_z$
is any element of
$g_z$
is any element of
![]() $G(\mathbb {R})^+$
sending
$G(\mathbb {R})^+$
sending
![]() $z_0$
to z. Let us denote by
$z_0$
to z. Let us denote by
![]() $L_g$
the left action of an element g in
$L_g$
the left action of an element g in
![]() $G(\mathbb {R})^+$
on
$G(\mathbb {R})^+$
on
![]() $\mathbb {D}^+$
. We also denote by
$\mathbb {D}^+$
. We also denote by
![]() $L_g$
the action on E given by
$L_g$
the action on E given by
![]() $L_{g}[g_z,v]=[gg_z,v]$
. The bundle is
$L_{g}[g_z,v]=[gg_z,v]$
. The bundle is
![]() $G(\mathbb {R})^+$
-equivariant with respect to these actions.
$G(\mathbb {R})^+$
-equivariant with respect to these actions.
Proposition 4.1 The section
![]() $s_v$
is well-defined and
$s_v$
is well-defined and
![]() $\Gamma _v$
-equivariant. Moreover, its zero locus is precisely
$\Gamma _v$
-equivariant. Moreover, its zero locus is precisely
![]() $\mathbb {D}^+_v$
.
$\mathbb {D}^+_v$
.
Proof The section is well-defined, since replacing
![]() $g_z$
by
$g_z$
by
![]() $g_zk$
gives
$g_zk$
gives
Suppose that z is in the zero locus of
![]() $s_v$
, that is to say
$s_v$
, that is to say
![]() $\textrm {pr}(g_z^{-1}v)$
vanishes. Then
$\textrm {pr}(g_z^{-1}v)$
vanishes. Then
![]() $g_z^{-1}v$
is in
$g_z^{-1}v$
is in
![]() $z_0^\perp $
. It is equivalent to the fact that
$z_0^\perp $
. It is equivalent to the fact that
![]() $z=g_zz_0$
is a subspace of
$z=g_zz_0$
is a subspace of
![]() $v^\perp $
, which means that z is in
$v^\perp $
, which means that z is in
![]() $\mathbb {D}_v^+$
. Hence, the zero locus of
$\mathbb {D}_v^+$
. Hence, the zero locus of
![]() $s_v$
is exactly
$s_v$
is exactly
![]() $\mathbb {D}^+_v$
. For the equivariance, note that we have
$\mathbb {D}^+_v$
. For the equivariance, note that we have
Hence, if
![]() $\gamma $
is an element of
$\gamma $
is an element of
![]() $\Gamma _v$
, we have
$\Gamma _v$
, we have
We define the pullback
![]() of the Mathai–Quillen form by
of the Mathai–Quillen form by
![]() $s_v$
. It defines a form
$s_v$
. It defines a form
It is only rapidly decreasing on
![]() $\mathbb {R}^q$
, and in order to make it rapidly decreasing everywhere we set
$\mathbb {R}^q$
, and in order to make it rapidly decreasing everywhere we set
It defines a form
![]() $ \varphi \in \mathscr {S}(\mathbb {R}^{p+q}) \otimes \Omega ^q(\mathbb {D})^+$
.
$ \varphi \in \mathscr {S}(\mathbb {R}^{p+q}) \otimes \Omega ^q(\mathbb {D})^+$
.
Proposition 4.2
-
(1) For fixed v in
 $V(\mathbb {R}),$
the form
$V(\mathbb {R}),$
the form
 $\varphi ^0(v)$
in
$\varphi ^0(v)$
in
 $\Omega ^q(\mathbb {D}^+)$
is given by (4.7)
$\Omega ^q(\mathbb {D}^+)$
is given by (4.7) $$ \begin{align} \varphi^0(v) & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \exp \left (-2 \sqrt{\pi} \nabla s_v+\rho(R)\right ). \end{align} $$
$$ \begin{align} \varphi^0(v) & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \exp \left (-2 \sqrt{\pi} \nabla s_v+\rho(R)\right ). \end{align} $$
-
(2) It satisfies
 $L_g^\ast \varphi ^0(v)=\varphi ^0(g^{-1}v)$
, hence (4.8)
$L_g^\ast \varphi ^0(v)=\varphi ^0(g^{-1}v)$
, hence (4.8) $$ \begin{align} \varphi^0 \in \left [\Omega^q(\mathbb{D}^+) \otimes C^\infty(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+}.\end{align} $$
$$ \begin{align} \varphi^0 \in \left [\Omega^q(\mathbb{D}^+) \otimes C^\infty(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+}.\end{align} $$
-
(3) It is a Poincaré dual of
 $\Gamma _v \backslash \mathbb {D}_v^+$
in
$\Gamma _v \backslash \mathbb {D}_v^+$
in
 $\Gamma _v \backslash \mathbb {D}^+$
.
$\Gamma _v \backslash \mathbb {D}^+$
.
Proof
-
(1) Recall that
 $\widetilde {\nabla }=\pi ^\ast \nabla $
and
$\widetilde {\nabla }=\pi ^\ast \nabla $
and
 $\widetilde {R}=\pi ^\ast R$
. We pullback by
$\widetilde {R}=\pi ^\ast R$
. We pullback by
 $s_v$
$s_v$

Since
 $\pi \circ s_v$
is the identity, we have (4.9)
$\pi \circ s_v$
is the identity, we have (4.9) $$ \begin{align} s_v^\ast \widetilde{\nabla} = s_v^\ast \pi^\ast \nabla = \nabla. \end{align} $$
$$ \begin{align} s_v^\ast \widetilde{\nabla} = s_v^\ast \pi^\ast \nabla = \nabla. \end{align} $$
Hence, the pullback connection
 $s_v^\ast \widetilde {\nabla }$
satisfies (4.10)since
$s_v^\ast \widetilde {\nabla }$
satisfies (4.10)since $$ \begin{align} s_v^\ast (\widetilde{\nabla} \mathbf{s})= (s_v^\ast \widetilde{\nabla}) ( s_v^\ast \mathbf{s}) = \nabla s_v, \end{align} $$
$$ \begin{align} s_v^\ast (\widetilde{\nabla} \mathbf{s})= (s_v^\ast \widetilde{\nabla}) ( s_v^\ast \mathbf{s}) = \nabla s_v, \end{align} $$
 $s_v^\ast \mathbf{s}=s_v$
. We also have
$s_v^\ast \mathbf{s}=s_v$
. We also have
 $s_v^\ast \widetilde {R}=R$
and (4.11)
$s_v^\ast \widetilde {R}=R$
and (4.11) $$ \begin{align}s_v^\ast \lVert \mathbf{s} \rVert^2= \lVert s_v \rVert^2= \langle s_v , s_v \rangle=-{Q\big|{}_{z_0} }(v,v). \end{align} $$
$$ \begin{align}s_v^\ast \lVert \mathbf{s} \rVert^2= \lVert s_v \rVert^2= \langle s_v , s_v \rangle=-{Q\big|{}_{z_0} }(v,v). \end{align} $$
The expression for
 $\varphi ^0$
then follows from the fact that
$\varphi ^0$
then follows from the fact that
 $\exp $
and
$\exp $
and
 $s_v^\ast $
commute.
$s_v^\ast $
commute. -
(2) The bundle E is
 $G(\mathbb {R})^+$
equivariant. By construction, the Mathai–Quillen form is
$G(\mathbb {R})^+$
equivariant. By construction, the Mathai–Quillen form is
 $G(\mathbb {R})^+$
-invariant, so
$G(\mathbb {R})^+$
-invariant, so
 $L_g^\ast U_{MQ}=U_{MQ}$
. On the other hand, we also have (4.12)
$L_g^\ast U_{MQ}=U_{MQ}$
. On the other hand, we also have (4.12) $$ \begin{align}s_v \circ L_g(z)=L_g \circ s_{g^{-1}v}(z),\end{align} $$
$$ \begin{align}s_v \circ L_g(z)=L_g \circ s_{g^{-1}v}(z),\end{align} $$
and thus,
(4.13) $$ \begin{align} L_g^\ast \varphi^0(v)=L_g^\ast s_v^\ast U_{MQ}=\varphi^0(g^{-1}v). \end{align} $$
$$ \begin{align} L_g^\ast \varphi^0(v)=L_g^\ast s_v^\ast U_{MQ}=\varphi^0(g^{-1}v). \end{align} $$
-
(3) Since
 $s_v$
is
$s_v$
is
 $\Gamma _v$
-equivariant, we view it as a section (4.14)whose zero locus is precisely
$\Gamma _v$
-equivariant, we view it as a section (4.14)whose zero locus is precisely $$ \begin{align} s_v \colon \Gamma_v \backslash \mathbb{D}^+ \longrightarrow \Gamma_v \backslash E, \end{align} $$
$$ \begin{align} s_v \colon \Gamma_v \backslash \mathbb{D}^+ \longrightarrow \Gamma_v \backslash E, \end{align} $$
 $\Gamma _v \backslash \mathbb {D}_v^+$
. Let
$\Gamma _v \backslash \mathbb {D}_v^+$
. Let
 $S_0$
(resp.
$S_0$
(resp.
 $S_v$
) be the image in
$S_v$
) be the image in
 $\Gamma _v \backslash E$
of the section
$\Gamma _v \backslash E$
of the section
 $s_v$
(resp. the zero section). By [Reference Bott and Tu2, Proposition 6.24(b)], the Thom form
$s_v$
(resp. the zero section). By [Reference Bott and Tu2, Proposition 6.24(b)], the Thom form
 $U_{MQ}$
is a Poincaré dual of the zero section
$U_{MQ}$
is a Poincaré dual of the zero section
 $S_0$
of E. For a form
$S_0$
of E. For a form
 $\omega $
in
$\omega $
in
 $\Omega _c^{m-q}(\Gamma _v \backslash \mathbb {D}^+),$
we have (4.15)
$\Omega _c^{m-q}(\Gamma _v \backslash \mathbb {D}^+),$
we have (4.15) $$ \begin{align} \int_{\Gamma_v \backslash \mathbb{D}^+} \varphi^0(v) \wedge \omega & = \int_{\Gamma_v \backslash \mathbb{D}^+} s_v^\ast \left ( U_{MQ} \wedge \pi ^\ast \omega \right ) \nonumber \\ & = \int_{S_v} U_{MQ} \wedge \pi ^\ast \omega \nonumber \\ & = \int_{S_v \cap S_0} \pi ^\ast \omega \nonumber \\ & = \int_{\Gamma_v \backslash \mathbb{D}_v^+} \omega. \end{align} $$
$$ \begin{align} \int_{\Gamma_v \backslash \mathbb{D}^+} \varphi^0(v) \wedge \omega & = \int_{\Gamma_v \backslash \mathbb{D}^+} s_v^\ast \left ( U_{MQ} \wedge \pi ^\ast \omega \right ) \nonumber \\ & = \int_{S_v} U_{MQ} \wedge \pi ^\ast \omega \nonumber \\ & = \int_{S_v \cap S_0} \pi ^\ast \omega \nonumber \\ & = \int_{\Gamma_v \backslash \mathbb{D}_v^+} \omega. \end{align} $$
The last step follows from the fact that
 $\pi ^{-1}(S_v \cap S_0)$
equals
$\pi ^{-1}(S_v \cap S_0)$
equals
 $\Gamma _v \backslash \mathbb {D}_v^+$
.
$\Gamma _v \backslash \mathbb {D}_v^+$
.
As in (2.19), we have an isomorphism
by evaluating at the basepoint
![]() $eK$
of
$eK$
of
![]() $G(\mathbb {R})^+/K$
that corresponds to
$G(\mathbb {R})^+/K$
that corresponds to
![]() $z_0$
in
$z_0$
in
![]() $\mathbb {D}^+$
. We will now compute
$\mathbb {D}^+$
. We will now compute
![]() ${ {\varphi ^0}\big|{}_{eK} }$
.
${ {\varphi ^0}\big|{}_{eK} }$
.
4.2 The Mathai–Quillen form at the identity
From now on, we identify
![]() $\mathbb {R}^{p+q}$
with
$\mathbb {R}^{p+q}$
with
![]() $V(\mathbb {R})$
by the orthonormal basis of (2.1), and let
$V(\mathbb {R})$
by the orthonormal basis of (2.1), and let
![]() $z_0$
be the negative spanned by the vectors
$z_0$
be the negative spanned by the vectors
![]() $e_{p+1}, \ldots , e_{p+q}$
. Hence, we identify
$e_{p+1}, \ldots , e_{p+q}$
. Hence, we identify
![]() $z_0$
with
$z_0$
with
![]() $\mathbb {R}^q$
and the quadratic form is
$\mathbb {R}^q$
and the quadratic form is
 $$ \begin{align} {Q\big|{}_{z_0} }(v,v)=-\sum_{\mu=p+1}^{p+q} x_\mu^2, \end{align} $$
$$ \begin{align} {Q\big|{}_{z_0} }(v,v)=-\sum_{\mu=p+1}^{p+q} x_\mu^2, \end{align} $$
where
![]() $x_{p+1}, \dots , x_{p+q}$
are the coordinates of the vector v.
$x_{p+1}, \dots , x_{p+q}$
are the coordinates of the vector v.
Let
![]() $f_v$
in
$f_v$
in
![]() $\Omega ^0(G(\mathbb {R})^+,z_0)^K$
be the map associated with the section
$\Omega ^0(G(\mathbb {R})^+,z_0)^K$
be the map associated with the section
![]() $s_v$
, as in Proposition 3.1. It is defined by
$s_v$
, as in Proposition 3.1. It is defined by
Then
![]() $df_v+\rho (\theta ) f_v$
is the horizontal lift of
$df_v+\rho (\theta ) f_v$
is the horizontal lift of
![]() $\nabla s_v$
, as discussed in Section 3.1. Let X be a vector in
$\nabla s_v$
, as discussed in Section 3.1. Let X be a vector in
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() $X_{\mathfrak {p}}$
and
$X_{\mathfrak {p}}$
and
![]() $X_{\mathfrak {k}}$
be its components with respect to the splitting of
$X_{\mathfrak {k}}$
be its components with respect to the splitting of
![]() $\mathfrak {g}$
as
$\mathfrak {g}$
as
![]() $\mathfrak {p} \oplus \mathfrak {k}$
. We have
$\mathfrak {p} \oplus \mathfrak {k}$
. We have
In particular, we can evaluate on the basis
![]() $X_{\alpha \mu }$
and get:
$X_{\alpha \mu }$
and get:
 $$ \begin{align} d_{e} f_v(X_{\alpha \mu}) & = \left. \frac{d}{dt} \right \rvert_{t=0} f_v(\exp tX_{\alpha \mu})\nonumber \\ & = -\operatorname{pr}(X_{\alpha \mu}v) \nonumber \\ & = -\operatorname{pr}(x_\mu e_\alpha+x_\alpha e_\mu) \nonumber\\ & = -x_{\alpha}e_\mu. \end{align} $$
$$ \begin{align} d_{e} f_v(X_{\alpha \mu}) & = \left. \frac{d}{dt} \right \rvert_{t=0} f_v(\exp tX_{\alpha \mu})\nonumber \\ & = -\operatorname{pr}(X_{\alpha \mu}v) \nonumber \\ & = -\operatorname{pr}(x_\mu e_\alpha+x_\alpha e_\mu) \nonumber\\ & = -x_{\alpha}e_\mu. \end{align} $$
So as an element of
![]() $\mathfrak {p}^\ast \otimes z_0$
, we can write
$\mathfrak {p}^\ast \otimes z_0$
, we can write
 $$ \begin{align}d_ef_v=-\sum_{\mu=p+1}^{p+q} \left ( \sum_{\alpha=1}^p x_\alpha \omega_{\alpha \mu} \right )\otimes e_\mu=-\sum_{\alpha=1}^p x_\alpha \eta_\alpha,\end{align} $$
$$ \begin{align}d_ef_v=-\sum_{\mu=p+1}^{p+q} \left ( \sum_{\alpha=1}^p x_\alpha \omega_{\alpha \mu} \right )\otimes e_\mu=-\sum_{\alpha=1}^p x_\alpha \eta_\alpha,\end{align} $$
with

Proposition 4.3 Let
![]() $\rho (R_e)$
in
$\rho (R_e)$
in
![]() $\wedge ^2\mathfrak {p}^\ast \otimes \mathfrak {so}(z_0)$
be the curvature at the identity. Then after identifying
$\wedge ^2\mathfrak {p}^\ast \otimes \mathfrak {so}(z_0)$
be the curvature at the identity. Then after identifying
![]() $\mathfrak {so}(z_0)$
with
$\mathfrak {so}(z_0)$
with
![]() $\wedge ^2 z_0$
, we have
$\wedge ^2 z_0$
, we have
 $$ \begin{align} \rho(R_e)= -\frac{1}{2} \sum_{\alpha=1}^p \eta_\alpha^2 \in \wedge^2\mathfrak{p}^\ast \otimes \wedge^2 z_0, \end{align} $$
$$ \begin{align} \rho(R_e)= -\frac{1}{2} \sum_{\alpha=1}^p \eta_\alpha^2 \in \wedge^2\mathfrak{p}^\ast \otimes \wedge^2 z_0, \end{align} $$
where
![]() $\eta _\alpha ^2=\eta _\alpha \wedge \eta _\alpha $
.
$\eta _\alpha ^2=\eta _\alpha \wedge \eta _\alpha $
.
Proof Using the relation
![]() $E_{ij}E_{kl}=\delta _{il}E_{kj}$
, one can show that
$E_{ij}E_{kl}=\delta _{il}E_{kj}$
, one can show that
for two vectors
![]() $X_{\alpha \nu }$
and
$X_{\alpha \nu }$
and
![]() $ X_{\beta \mu }$
in
$ X_{\beta \mu }$
in
![]() $\mathfrak {p}$
. Hence, we have
$\mathfrak {p}$
. Hence, we have
 $$ \begin{align} R_e(X_{\alpha \nu} \wedge X_{\beta \mu}) & =[\theta(X_{\alpha \nu}), \theta(X_{\beta \mu})] -\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-p\left (\delta_{\alpha \beta}X_{\nu \mu}+\delta_{\nu \mu}X_{\alpha \beta} \right ) \nonumber \\ & = -\delta_{\alpha \beta}X_{\nu \mu}. \end{align} $$
$$ \begin{align} R_e(X_{\alpha \nu} \wedge X_{\beta \mu}) & =[\theta(X_{\alpha \nu}), \theta(X_{\beta \mu})] -\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-p\left (\delta_{\alpha \beta}X_{\nu \mu}+\delta_{\nu \mu}X_{\alpha \beta} \right ) \nonumber \\ & = -\delta_{\alpha \beta}X_{\nu \mu}. \end{align} $$
On the other hand, since
![]() $\eta _i(X_{jr})=\delta _{ij}e_r$
, we also have
$\eta _i(X_{jr})=\delta _{ij}e_r$
, we also have
 $$ \begin{align} \sum_{i=1}^p \eta_i^2(X_{\alpha \nu} \wedge X_{\beta \mu}) & = \sum_{i=1}^p \eta_i(X_{\alpha \nu}) \wedge \eta_i(X_{\beta \mu})-\eta_i(X_{\beta \mu}) \wedge \eta_i(X_{\alpha \nu}) \nonumber \\ & =2 \delta_{\alpha \beta}e_\nu \wedge e_\mu. \end{align} $$
$$ \begin{align} \sum_{i=1}^p \eta_i^2(X_{\alpha \nu} \wedge X_{\beta \mu}) & = \sum_{i=1}^p \eta_i(X_{\alpha \nu}) \wedge \eta_i(X_{\beta \mu})-\eta_i(X_{\beta \mu}) \wedge \eta_i(X_{\alpha \nu}) \nonumber \\ & =2 \delta_{\alpha \beta}e_\nu \wedge e_\mu. \end{align} $$
The lemma follows since
![]() $\rho (X_{\nu \mu })=T(e_\nu \wedge e_\mu )$
in
$\rho (X_{\nu \mu })=T(e_\nu \wedge e_\mu )$
in
![]() $\mathfrak {so}(z_0)$
, because
$\mathfrak {so}(z_0)$
, because
Using the fact that the exponential satisfies
![]() $\exp (\omega +\eta )=\exp (\omega )\exp (\eta )$
on the subalgebra
$\exp (\omega +\eta )=\exp (\omega )\exp (\eta )$
on the subalgebra
![]() $\bigoplus \Omega ^{i,i}$
—see Remark 3.1—we can write
$\bigoplus \Omega ^{i,i}$
—see Remark 3.1—we can write
 $$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) &= (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \prod_{\alpha=1}^p \exp \left ( 2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ). \end{align} $$
$$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) &= (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \prod_{\alpha=1}^p \exp \left ( 2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ). \end{align} $$
We define the nth Hermite polynomial by
The first three Hermite polynomials are
![]() $H_0(x)=1$
,
$H_0(x)=1$
,
![]() $H_1(x)=2x$
, and
$H_1(x)=2x$
, and
![]() $H_2(x)=4x^2-2$
.
$H_2(x)=4x^2-2$
.
Lemma 4.4 Let
![]() $\eta $
be a form in
$\eta $
be a form in
![]() $\bigoplus \Omega ^{i,i}$
. Then
$\bigoplus \Omega ^{i,i}$
. Then
where
![]() $H_n$
is the nth Hermite polynomial.
$H_n$
is the nth Hermite polynomial.
Proof Since
![]() $\eta $
and
$\eta $
and
![]() $\eta ^2$
are in
$\eta ^2$
are in
![]() $\bigoplus \Omega ^{i,i}$
, they commute and we can use the binomial formula:
$\bigoplus \Omega ^{i,i}$
, they commute and we can use the binomial formula:
 $$ \begin{align} \exp(2x \eta-\eta^2) & =\sum_{k \geq 0} \frac{1}{k!} \left (2x\eta-\eta^2 \right)^k \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x \eta)^{k-l}\left (-\eta^2 \right)^{l} \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x)^{k-l} (- 1 )^{l} \eta^{l+k} \nonumber \\ & = \sum_{n \geq 0} P_n(x)\eta^n, \end{align} $$
$$ \begin{align} \exp(2x \eta-\eta^2) & =\sum_{k \geq 0} \frac{1}{k!} \left (2x\eta-\eta^2 \right)^k \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x \eta)^{k-l}\left (-\eta^2 \right)^{l} \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x)^{k-l} (- 1 )^{l} \eta^{l+k} \nonumber \\ & = \sum_{n \geq 0} P_n(x)\eta^n, \end{align} $$
where

The conditions on k and l imply that n is less than or equal to
![]() $2k$
. First, suppose that n is even. Then we have that k is between
$2k$
. First, suppose that n is even. Then we have that k is between
![]() $\frac {n}{2}$
and n, so that the sum above can be written
$\frac {n}{2}$
and n, so that the sum above can be written
 $$ \begin{align} \sum_{k=\frac{n}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n}{2}}\frac{(-1)^{\frac{n}{2}-m}}{(\frac{n}{2}-m)!(2m)!} (2x)^{2m}=\frac{1}{n!}H_n(x), \end{align} $$
$$ \begin{align} \sum_{k=\frac{n}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n}{2}}\frac{(-1)^{\frac{n}{2}-m}}{(\frac{n}{2}-m)!(2m)!} (2x)^{2m}=\frac{1}{n!}H_n(x), \end{align} $$
where in the second step, we let m be
![]() $k-\frac {n}{2}$
. If n is odd, then k is between
$k-\frac {n}{2}$
. If n is odd, then k is between
![]() $\frac {n+1}{2}$
and n, so that the sum can be written
$\frac {n+1}{2}$
and n, so that the sum can be written
 $$ \begin{align} \sum_{k=\frac{n+1}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n-1}{2}}\frac{(-1)^{\frac{n-1}{2}-m}}{(\frac{n-1}{2}-m)!(2m+1)!} (2x)^{2m+1}=\frac{1}{n!}H_n(x). \end{align} $$
$$ \begin{align} \sum_{k=\frac{n+1}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n-1}{2}}\frac{(-1)^{\frac{n-1}{2}-m}}{(\frac{n-1}{2}-m)!(2m+1)!} (2x)^{2m+1}=\frac{1}{n!}H_n(x). \end{align} $$
Applying the lemma to (4.28), we get
 $$ \begin{align} & \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ) \nonumber \\ &= \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{2\pi}x_\alpha \frac{\eta_\alpha}{\sqrt{2}}-\left (\frac{\eta_\alpha}{\sqrt{2}}\right)^2 \right ) \nonumber \\ & = \int^B \prod_{\alpha=1}^p \sum_{n \geq 0} \frac{2^{-n/2}}{n!}H_n\left (\sqrt{2\pi} x_\alpha \right )\eta_\alpha^n \nonumber \\ & = \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right ) \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$
$$ \begin{align} & \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ) \nonumber \\ &= \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{2\pi}x_\alpha \frac{\eta_\alpha}{\sqrt{2}}-\left (\frac{\eta_\alpha}{\sqrt{2}}\right)^2 \right ) \nonumber \\ & = \int^B \prod_{\alpha=1}^p \sum_{n \geq 0} \frac{2^{-n/2}}{n!}H_n\left (\sqrt{2\pi} x_\alpha \right )\eta_\alpha^n \nonumber \\ & = \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right ) \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$
If
![]() $n_1+ \cdots + n_p$
is different from q, then the Berezinian of
$n_1+ \cdots + n_p$
is different from q, then the Berezinian of
![]() $\eta _1^{n_1} \wedge \cdots \wedge \eta _p^{n_p}$
vanishes and we get
$\eta _1^{n_1} \wedge \cdots \wedge \eta _p^{n_p}$
vanishes and we get
 $$ \begin{align} & \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right )\int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ = & 2^{-\frac{q}{2}}\sum_{n_1+ \dots+ n_p=q}\frac{H_{n_1}\left (\sqrt{2\pi}x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )}{n_1! \ldots n_p!} \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$
$$ \begin{align} & \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right )\int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ = & 2^{-\frac{q}{2}}\sum_{n_1+ \dots+ n_p=q}\frac{H_{n_1}\left (\sqrt{2\pi}x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )}{n_1! \ldots n_p!} \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$
Note that
 $$ \begin{align} \eta_\alpha^{n_\alpha} & = \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \sum_{\mu_1, \dots, \mu_{n_\alpha}} (\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}), \end{align} $$
$$ \begin{align} \eta_\alpha^{n_\alpha} & = \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \sum_{\mu_1, \dots, \mu_{n_\alpha}} (\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}), \end{align} $$
where the sums are over all
![]() $\mu _i$
’s between
$\mu _i$
’s between
![]() $p+1$
and
$p+1$
and
![]() $p+q$
. If
$p+q$
. If
![]() $n_1+\cdots +n_p$
is equal to
$n_1+\cdots +n_p$
is equal to
![]() $q,$
we have
$q,$
we have
 $$ \begin{align} & \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_1! \ldots n_p! \sum \int^B (\omega_{\alpha (p+1)} \otimes e_{1}) \wedge \cdots \wedge (\omega_{\alpha (p+q)} \otimes e_{q}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} n_1! \ldots n_p! \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)}, \end{align} $$
$$ \begin{align} & \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_1! \ldots n_p! \sum \int^B (\omega_{\alpha (p+1)} \otimes e_{1}) \wedge \cdots \wedge (\omega_{\alpha (p+q)} \otimes e_{q}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} n_1! \ldots n_p! \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)}, \end{align} $$
where the sums in the last two lines go over all tuples
![]() $\underline {\alpha }=(\alpha _1, \dots , \alpha _q)$
with
$\underline {\alpha }=(\alpha _1, \dots , \alpha _q)$
with
![]() $\alpha $
between
$\alpha $
between
![]() $1$
and p, and the value
$1$
and p, and the value
![]() $\alpha $
appears exactly
$\alpha $
appears exactly
![]() $n_{\alpha }$
-times in
$n_{\alpha }$
-times in
![]() $\underline {\alpha }$
. Hence
$\underline {\alpha }$
. Hence
 $$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}}\sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (2\pi {Q\big|{}_{z_0} }(v,v) \right ). \nonumber \end{align} $$
$$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}}\sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (2\pi {Q\big|{}_{z_0} }(v,v) \right ). \nonumber \end{align} $$
After multiplying by
![]() $\exp \left (-\pi Q(v,v) \right )$
, we get
$\exp \left (-\pi Q(v,v) \right )$
, we get
 $$ \begin{align} {{\varphi}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right )\\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi Q_{z_0}^+(v,v) \right ). \nonumber \end{align} $$
$$ \begin{align} {{\varphi}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right )\\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi Q_{z_0}^+(v,v) \right ). \nonumber \end{align} $$
The form is now rapidly decreasing in v, since the Siegel majorant is positive definite. We have
Theorem 4.5 We have
![]() $2^{-\frac {q}{2}}\varphi (v)=\varphi _{KM}(v)$
.
$2^{-\frac {q}{2}}\varphi (v)=\varphi _{KM}(v)$
.
Proof It is a straightforward computation to show that
 $$ \begin{align} (2 \pi)^{-n_\alpha/2}H_{n_\alpha}\left ( \sqrt{2 \pi}x_\alpha \right )\exp(-\pi x_\alpha^2) & = \left (x_\alpha - \frac{1}{2\pi}\frac{\partial}{\partial{x_\alpha}} \right )^{n_\alpha} \exp(-\pi x_\alpha^2). \end{align} $$
$$ \begin{align} (2 \pi)^{-n_\alpha/2}H_{n_\alpha}\left ( \sqrt{2 \pi}x_\alpha \right )\exp(-\pi x_\alpha^2) & = \left (x_\alpha - \frac{1}{2\pi}\frac{\partial}{\partial{x_\alpha}} \right )^{n_\alpha} \exp(-\pi x_\alpha^2). \end{align} $$
Hence, applying this, we find that the Kudla–Millson form, defined by the Howe operators in (2.22), is
 $$ \begin{align} {{\varphi_{KM}}\big|{}_{e} }(v) & = 2^{-q}(2\pi)^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi {Q\big|{}_{z_0} }(v,v) \right ) \nonumber \\ & = 2^{-\frac{q}{2}} e^{-\pi Q(v,v)}{{\varphi^0}\big|{}_{e} }(v).\nonumber\\[-34pt]\nonumber \end{align} $$
$$ \begin{align} {{\varphi_{KM}}\big|{}_{e} }(v) & = 2^{-q}(2\pi)^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi {Q\big|{}_{z_0} }(v,v) \right ) \nonumber \\ & = 2^{-\frac{q}{2}} e^{-\pi Q(v,v)}{{\varphi^0}\big|{}_{e} }(v).\nonumber\\[-34pt]\nonumber \end{align} $$
5 Examples and remarks
-
(1) Let us compute the Kudla–Millson as above in the simplest setting of signature
 $(1,1)$
. Let
$(1,1)$
. Let
 $V(\mathbb {R})$
be the quadratic space
$V(\mathbb {R})$
be the quadratic space
 $\mathbb {R}^2$
with the quadratic form
$\mathbb {R}^2$
with the quadratic form
 $Q(v,w)=x'y+xy'$
, where x and
$Q(v,w)=x'y+xy'$
, where x and
 $x'$
(resp. y and
$x'$
(resp. y and
 $y'$
) are the components of v (respectively of w). Let
$y'$
) are the components of v (respectively of w). Let
 $e_1=\frac {1}{\sqrt {2}}(1,1)$
and
$e_1=\frac {1}{\sqrt {2}}(1,1)$
and
 $e_2=\frac {1}{\sqrt {2}}(1,-1)$
. The one-dimensional negative plane
$e_2=\frac {1}{\sqrt {2}}(1,-1)$
. The one-dimensional negative plane
 $z_0$
is
$z_0$
is
 $\mathbb {R} e_2$
. If r denotes the variable on
$\mathbb {R} e_2$
. If r denotes the variable on
 $z_0$
, then the quadratic form is
$z_0$
, then the quadratic form is
 ${{Q}\big|{}_{z_0} }(r)=-r^2$
. The projection map is given by (5.1)
${{Q}\big|{}_{z_0} }(r)=-r^2$
. The projection map is given by (5.1) $$ \begin{align} \operatorname{pr} \colon V(\mathbb{R}) & \longrightarrow z_0 \nonumber \\ v=(x,x') & \longmapsto \frac{x-x'}{\sqrt{2}}. \end{align} $$
$$ \begin{align} \operatorname{pr} \colon V(\mathbb{R}) & \longrightarrow z_0 \nonumber \\ v=(x,x') & \longmapsto \frac{x-x'}{\sqrt{2}}. \end{align} $$
The orthogonal group of
 $V(\mathbb {R})$
is (5.2)and
$V(\mathbb {R})$
is (5.2)and $$ \begin{align} G(\mathbb{R})^+=\left \{ \begin{pmatrix} t & 0 \\ 0 & t^{-1} \end{pmatrix},t>0 \right \}, \end{align} $$
$$ \begin{align} G(\mathbb{R})^+=\left \{ \begin{pmatrix} t & 0 \\ 0 & t^{-1} \end{pmatrix},t>0 \right \}, \end{align} $$
 $\mathbb {D}^+$
can be identified with
$\mathbb {D}^+$
can be identified with
 $\mathbb {R}_{>0}$
. The associated bundle E is
$\mathbb {R}_{>0}$
. The associated bundle E is
 $\mathbb {R}_{>0} \times \mathbb {R}$
and the connection
$\mathbb {R}_{>0} \times \mathbb {R}$
and the connection
 $\nabla $
is simply d since the bundle is trivial. Hence, the Mathai–Quillen form is (5.3)as in the proof of Proposition 3.5. The section
$\nabla $
is simply d since the bundle is trivial. Hence, the Mathai–Quillen form is (5.3)as in the proof of Proposition 3.5. The section $$ \begin{align} U_{MQ}=\sqrt{2}e^{-2\pi r^2}dr \in \Omega^1(E), \end{align} $$
$$ \begin{align} U_{MQ}=\sqrt{2}e^{-2\pi r^2}dr \in \Omega^1(E), \end{align} $$
 $s_v \colon \mathbb {R}_{>0} \rightarrow E$
is given by (5.4)where x and
$s_v \colon \mathbb {R}_{>0} \rightarrow E$
is given by (5.4)where x and $$ \begin{align} s_v(t)=\left (t, \frac{t^{-1}x-tx'}{\sqrt{2}} \right ), \end{align} $$
$$ \begin{align} s_v(t)=\left (t, \frac{t^{-1}x-tx'}{\sqrt{2}} \right ), \end{align} $$
 $x'$
are the components of v. We obtain (5.5)
$x'$
are the components of v. We obtain (5.5) $$ \begin{align} s_v^\ast U_{MQ}=e^{-\pi \left ( \frac{x}{t}-tx' \right )^2}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$
$$ \begin{align} s_v^\ast U_{MQ}=e^{-\pi \left ( \frac{x}{t}-tx' \right )^2}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$
Hence, after multiplication by
 $2^{-\frac {1}{2}}e^{-\pi Q(v,v)}$
, we get (5.6)
$2^{-\frac {1}{2}}e^{-\pi Q(v,v)}$
, we get (5.6) $$ \begin{align} \varphi_{KM}(x,x')= 2^{-\frac{1}{2}}e^{-\pi \left [ \left (\frac{x}{t} \right )^2+(tx')^2 \right ]}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$
$$ \begin{align} \varphi_{KM}(x,x')= 2^{-\frac{1}{2}}e^{-\pi \left [ \left (\frac{x}{t} \right )^2+(tx')^2 \right ]}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$
-
(2) The second example illustrates the functorial properties of the Mathai–Quillen form. Suppose that we have an orthogonal splitting of
 $V(\mathbb {R})$
as
$V(\mathbb {R})$
as
 $\bigoplus _i^r V_i(\mathbb {R})$
. Let
$\bigoplus _i^r V_i(\mathbb {R})$
. Let
 $(p_i,q_i)$
be the signature of
$(p_i,q_i)$
be the signature of
 $V_i(\mathbb {R})$
. We have (5.7)
$V_i(\mathbb {R})$
. We have (5.7) $$ \begin{align} \mathbb{D}_{1} \times \cdots \times \mathbb{D}_{r} \simeq \left \{ z \in \mathbb{D} \; \vert \; z = \bigoplus_{i=1}^r z \cap V_i(\mathbb{R}) \right \}. \end{align} $$
$$ \begin{align} \mathbb{D}_{1} \times \cdots \times \mathbb{D}_{r} \simeq \left \{ z \in \mathbb{D} \; \vert \; z = \bigoplus_{i=1}^r z \cap V_i(\mathbb{R}) \right \}. \end{align} $$
Suppose, we fix
 $z_0= z_0^1 \oplus \cdots \oplus z_0^r$
in
$z_0= z_0^1 \oplus \cdots \oplus z_0^r$
in
 $\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r} \subset \mathbb {D}$
, where
$\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r} \subset \mathbb {D}$
, where
 $z_0^i$
is a negative
$z_0^i$
is a negative
 $q_i$
-plane in
$q_i$
-plane in
 $V_i(\mathbb {R})$
. Let
$V_i(\mathbb {R})$
. Let
 $G_i(\mathbb {R})$
be the subgroup preserving
$G_i(\mathbb {R})$
be the subgroup preserving
 $V_i(\mathbb {R})$
, let
$V_i(\mathbb {R})$
, let
 $K_i$
be the stabilizer of
$K_i$
be the stabilizer of
 $z_0^i$
, and
$z_0^i$
, and
 $\mathbb {D}_i$
be the symmetric space associated with
$\mathbb {D}_i$
be the symmetric space associated with
 $V_i(\mathbb {R})$
.
$V_i(\mathbb {R})$
.Over
 $\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r}$
the bundle E splits as an orthogonal sum
$\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r}$
the bundle E splits as an orthogonal sum
 $E_1 \oplus \cdots \oplus E_r$
, where
$E_1 \oplus \cdots \oplus E_r$
, where
 $E_i$
is the bundle
$E_i$
is the bundle
 $G_i(\mathbb {R})^+ \times _{K_i} z_0^i$
. Moreover, the restriction of the Mathai–Quillen form to this subbundle is (5.8)where
$G_i(\mathbb {R})^+ \times _{K_i} z_0^i$
. Moreover, the restriction of the Mathai–Quillen form to this subbundle is (5.8)where $$ \begin{align} {{U_{MQ}}\big|{}_{E_1 \times \cdots \times E_r} }=U_{MQ}^1 \wedge \cdots \wedge U_{MQ}^r, \end{align} $$
$$ \begin{align} {{U_{MQ}}\big|{}_{E_1 \times \cdots \times E_r} }=U_{MQ}^1 \wedge \cdots \wedge U_{MQ}^r, \end{align} $$
 $U_{MQ}^i$
is the Mathai–Quillen form on
$U_{MQ}^i$
is the Mathai–Quillen form on
 $E_i$
. The section
$E_i$
. The section
 $s_v$
also splits as a direct sum
$s_v$
also splits as a direct sum
 $\oplus s_{v_i}$
, where
$\oplus s_{v_i}$
, where
 $v_i$
is the projection of v onto
$v_i$
is the projection of v onto
 $v_i$
. In summary, the following diagram commutes (5.9)and we can conclude that
$v_i$
. In summary, the following diagram commutes (5.9)and we can conclude that (5.10)where
(5.10)where $$ \begin{align} {{\varphi_{KM}(v)}\big|{}_{\mathbb{D}_1^+ \times \cdots \times \mathbb{D}_r^+} }=\varphi_{KM}^1(v_1)\wedge \cdots \wedge \varphi_{KM}^r(v_r), \end{align} $$
$$ \begin{align} {{\varphi_{KM}(v)}\big|{}_{\mathbb{D}_1^+ \times \cdots \times \mathbb{D}_r^+} }=\varphi_{KM}^1(v_1)\wedge \cdots \wedge \varphi_{KM}^r(v_r), \end{align} $$
 $\varphi _{KM}^i$
is the Kudla–Millson form on
$\varphi _{KM}^i$
is the Kudla–Millson form on
 $\mathbb {D}_i^+$
.
$\mathbb {D}_i^+$
.
-
(2) Let
 $U \subset V$
be a nondegenerate r-subspace spanned by vectors
$U \subset V$
be a nondegenerate r-subspace spanned by vectors
 $v_1, \dots , v_r$
. Let
$v_1, \dots , v_r$
. Let
 $(p',q')$
be the signature of U. Let
$(p',q')$
be the signature of U. Let
 $\mathbb {D}_U$
be the subspace (5.11)
$\mathbb {D}_U$
be the subspace (5.11)
When U is positive, i.e., when
 $q'=0$
, then
$q'=0$
, then
 $\mathbb {D}_U$
is in fact (5.12)
$\mathbb {D}_U$
is in fact (5.12)
In particular, when U is spanned by a single positive vector v, then
 $\mathbb {D}_U=\mathbb {D}_v$
, where
$\mathbb {D}_U=\mathbb {D}_v$
, where
 $\mathbb {D}_v$
is as in (2.4). Kudla and Millson construct an
$\mathbb {D}_v$
is as in (2.4). Kudla and Millson construct an
 $rq$
-form
$rq$
-form
 $\varphi _{KM}(v_1,\dots ,v_r)$
that is a Poincaré dual to
$\varphi _{KM}(v_1,\dots ,v_r)$
that is a Poincaré dual to
 $\Gamma _U \backslash \mathbb {D}_U$
in
$\Gamma _U \backslash \mathbb {D}_U$
in
 $\Gamma _U \backslash \mathbb {D}$
, where
$\Gamma _U \backslash \mathbb {D}$
, where
 $\Gamma _U$
is the stabilizer of U in
$\Gamma _U$
is the stabilizer of U in
 $\Gamma $
. One of its properties [Reference Kudla and Millson8][Lemma. 4.1] is that (5.13)
$\Gamma $
. One of its properties [Reference Kudla and Millson8][Lemma. 4.1] is that (5.13) $$ \begin{align} \varphi_{KM}(v_1,\dots,v_r)=\varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r). \end{align} $$
$$ \begin{align} \varphi_{KM}(v_1,\dots,v_r)=\varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r). \end{align} $$
Let us explain how this form can also be recovered by the Mathai–Quillen formalism. Consider the bundle
 $E^r=E \oplus \cdots \oplus E$
of rank
$E^r=E \oplus \cdots \oplus E$
of rank
 $rq$
over
$rq$
over
 $\mathbb {D}$
. One can check that all the “ingredients” of the Mathai–Quillen form
$\mathbb {D}$
. One can check that all the “ingredients” of the Mathai–Quillen form
 $U_{MQ}(E^r)$
are compatible with respect to the splitting as a direct sum, so that we have (5.14)
$U_{MQ}(E^r)$
are compatible with respect to the splitting as a direct sum, so that we have (5.14) $$ \begin{align} U_{MQ}(E^r)=U_{MQ}(E) \wedge \dots \wedge U_{MQ}(E). \end{align} $$
$$ \begin{align} U_{MQ}(E^r)=U_{MQ}(E) \wedge \dots \wedge U_{MQ}(E). \end{align} $$
On the other hand, the zero locus of the section
 of
of
 $E^r$
is precisely
$E^r$
is precisely
 $\mathbb {D}_U$
. Hence, the pullback (5.15)is a Poincaré dual of
$\mathbb {D}_U$
. Hence, the pullback (5.15)is a Poincaré dual of
 $\mathbb {D}_U$
. Moreover, by (5.14), we have (5.16)
$\mathbb {D}_U$
. Moreover, by (5.14), we have (5.16) $$ \begin{align} \varphi^0(v_1,\dots,v_r)=\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r). \end{align} $$
$$ \begin{align} \varphi^0(v_1,\dots,v_r)=\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r). \end{align} $$
Finally, after setting
(5.17)we get (5.18)
(5.18) $$ \begin{align} 2^{-\frac{rq}{2}}\varphi(v_1,\dots, v_r) & = 2^{-\frac{rq}{2}} e^{-\pi \sum_{i=1}^r Q(v_i,v_i) }\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r) \nonumber\\ & = 2^{-\frac{rq}{2}} \varphi(v_1) \wedge \cdots \wedge \varphi(v_r) \nonumber\\ & = \varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r) \nonumber \\ & = \varphi_{KM}(v_1,\dots,v_r). \end{align} $$
$$ \begin{align} 2^{-\frac{rq}{2}}\varphi(v_1,\dots, v_r) & = 2^{-\frac{rq}{2}} e^{-\pi \sum_{i=1}^r Q(v_i,v_i) }\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r) \nonumber\\ & = 2^{-\frac{rq}{2}} \varphi(v_1) \wedge \cdots \wedge \varphi(v_r) \nonumber\\ & = \varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r) \nonumber \\ & = \varphi_{KM}(v_1,\dots,v_r). \end{align} $$
Acknowledgment
This project is part of my thesis and I thank my advisors Nicolas Bergeron and Luis Garcia for suggesting me this topic and for their support. I thank the anonymous referee for helpful comments and suggestions.