Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:51:57.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Iterated Limits of Lattices

Published online by Cambridge University Press:  20 November 2018

Craig Platt
Craig Platt*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the results of [5] are extended to classes of lattices. We assume familiarity with [5], but we recall for convenience the principal definitions and notations. If 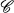is a category and if 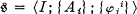is a direct [resp., inverse] limit system in 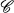, then 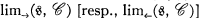is the direct [resp., inverse] limit of (determined only up to isomorphism in 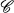). If is an inverse limit system of sets or universal algebras, let 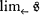denote the canonical construction of inverse limit described for example in [1, Chapter 3].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1301 - 1320
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Grätzer, G., Universal algebra (Van Nostrand Reinhold, Princeton, N.J., 1968).Google Scholar
2. Hedrlín, Z. and Pultr, A., On full embeddings of categories of algebras, Illinois J. Math. 10 (1966), 392–406.Google Scholar
3. Hedrlín, Z. and Vopĕnka, P., An undecidable theorem concerning full embeddings into categories of algebras, Comment. Math. Univ. Carolinae 7 (1966), 401–409.Google Scholar
4. Platt, C. R., Iterated limits of universal algebras, Ph.D. Thesis, Pennsylvania State University, 1969.Google Scholar
5. Platt, C. R., Iterated limits of universal algebras, Algebra Universalis 1 (1971), 167–181.Google Scholar