Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T00:00:24.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse Problems for Partition Functions

Published online by Cambridge University Press:  20 November 2018

Yifan Yang
Yifan Yang*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 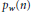${{p}_{w}}(n)$ be the weighted partition function defined by the generating function 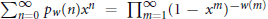$\Sigma _{n=0}^{\infty }{{p}_{w}}(n){{x}^{n}}=\prod{_{m=1}^{\infty }{{(1-{{x}^{m}})}^{-w(m)}}}$ , where 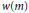$w\left( m \right)$ is a non-negative arithmetic function. Let 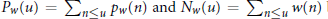${{P}_{w}}(u)={{\Sigma }_{n\le u}}{{p}_{w}}(n)\,and\,{{N}_{w}}(u)={{\Sigma }_{n\le u}}w(n)$ be the summatory functions for 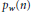${{p}_{w}}(n)$ and 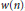$w\left( n \right)$, respectively. Generalizing results of G. A. Freiman and E. E. Kohlbecker, we show that, for a large class of functions 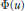$\Phi \left( u \right)$ and 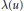$\text{ }\!\!\lambda\!\!\text{ }\left( u \right)$, an estimate for 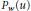${{P}_{w}}\left( u \right)$ of the form log 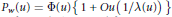${{P}_{w}}(u)=\Phi (u)\{1+Ou(1/\lambda (u))\}$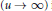$\left( u\to \infty \right)$ implies an estimate for 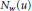${{N}_{w}}(u)$ of the form ${{N}_{w}}(u)={{\Phi }^{*}}(u)\{1+O(1/\log \lambda (u))\}$$\left( u\to \infty \right)$ with a suitable function ${{\Phi }^{*}}(u)$ defined in terms of $\Phi \left( u \right)$. We apply this result and related results to obtain characterizations of the Riemann Hypothesis and the Generalized Riemann Hypothesis in terms of the asymptotic behavior of certain weighted partition functions.

Keywords

11P8211M2640E05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 4 , 01 August 2001 , pp. 866 - 896
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Andrews, G. E., The theory of partitions. Cambridge University Press, Cambridge, 1998, reprint.Google Scholar
[2] Brigham, N. A., A general asymptotic formula for partition functions. Proc. Amer. Math. Soc. 1(1950), 182–191.Google Scholar
[3] Erdős, P., On an elementary proof of some asymptotic formulas in the theory of partitions. Ann. of Math. (2) 43(1942), 437–450.Google Scholar
[4] Freiman, G. A., Inverse problems of the additive theory of numbers. Izv. Akad. SSSR. Ser. Mat. 19(1955), 275–284.Google Scholar
[5] Geluk, J. L., Asymptotically balanced functions and the asymptotic behavior of the complementary function and the Laplace transform. J. Math. Anal. Appl. 139(1989), 226–242.Google Scholar
[6] Geluk, J. L., An Abel-Tauber theorem for partitions. Proc. Amer.Math. Soc. 82(1981), 571–575.Google Scholar
[7] Geluk, J. L., An Abel-Tauber theorem for partitions. II. J. Number Theory 33(1989), 170–181.Google Scholar
[8] Hardy, G. H. and Ramanujan, S., Asymptotic formulae for the distribution of integers of various types. Proc. London Math. Soc. 16(1917), 112–132.Google Scholar
[9] Hardy, G. H. and Ramanujan, S., Asymptotic formulae in combinatory analysis. Proc. LondonMath. Soc. 17(1918), 75–115.Google Scholar
[10] Ingham, A. E., A Tauberian theorem for partitions. Ann. of Math. 42(1941), 1075–1090.Google Scholar
[11] Ingham, A. E., The distribution of prime numbers. Cambridge University Press, Cambridge, 1990.Google Scholar
[12] Kohlbecker, E. E., Weak asymptotic properties of partitions. Trans. Amer. Math. Soc. 88(1958), 346–365.Google Scholar
[13] Meinardus, G., Asymptotische Aussagen über Partitionen. Math. Z. 59(1954), 388–398.Google Scholar
[14] Meinardus, G., Über Partitionen mit Differenzenbedingungen. Math. Z. 61(1954), 289–302.Google Scholar
[15] Omey, E., Tauberian theorems with remainder. J. LondonMath. Soc. (2) 32(1985), 116–132.Google Scholar
[16] Parameswaran, S., Partition functions whose logarithms are slowly oscillating. Trans. Amer. Math. Soc. 100(1961), 217–240.Google Scholar
[17] Prachar, K., Primzahlverteilung. Springer-Verlag, Berlin, Göttingen, Heidelberg, 1957.Google Scholar
[18] Richmond, B., Asymptotic relations for partitions. J. Number Theory 7(1975), 389–405.Google Scholar
[19] Richmond, B., A general asymptotic result for partitions. Canad. J. Math. 27(1975), 1083–1091.Google Scholar
[20] Roth, K. F. and Szekeres, G., Some asymptotic formulae in the theory of partitions. Quart. J. Math. Oxford Ser. (2) 5(1954), 241–259.Google Scholar
[21] Schwarz, W., Schwache asymptotische Eigenschaften von Partitionen. J. Reine Angew.Math. 232(1968), 1–16.Google Scholar
[22] Schwarz, W., Asymptotische Formeln für Partitionen. J. Reine Angew.Math. 234(1969), 174–178.Google Scholar
[23] Tenenbaum, G., Introduction to analytic and probabilistic number theory. 2nd ed., Cambridge University Press, Cambridge, 1995.Google Scholar
[24] Titchmarsh, E. C., The theory of the Riemann zeta-function. 2nd ed., The Clarendon Press, Oxford University Press, New York, 1986.Google Scholar
[25] Yang, Y., Partitions into primes. Trans. Amer. Math. Soc. 352(2000), 2581–2600.Google Scholar