Assuming Lang's conjectured lower bound on the heights of non-torsion points on an elliptic curve, we show that there exists an absolute constant 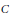$C$ such that for any elliptic curve 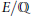$E/\mathbb{Q}$ and non-torsion point 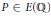$P\,\in \,E\left( \mathbb{Q} \right)$, there is at most one integral multiple 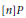$\left[ n \right]P$ such that 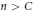$n\,>\,C$. The proof is a modification of a proof of Ingram giving an unconditional, but not uniform, bound. The new ingredient is a collection of explicit formulæ for the sequence 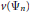$v\left( {{\Psi }_{n}} \right)$ of valuations of the division polynomials. For 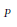$P$ of non-singular reduction, such sequences are already well described in most cases, but for 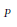$P$ of singular reduction, we are led to define a new class of sequences called elliptic troublemaker sequences, which measure the failure of the Néron local height to be quadratic. As a corollary in the spirit of a conjecture of Lang and Hall, we obtain a uniform upper bound on 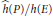$\widehat{h}\left( P \right)/h\left( E \right)$ for integer points having two large integral multiples.