Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T14:03:14.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for Rational Functions With Prescribed Poles

Published online by Cambridge University Press:  20 November 2018

G. Min
G. Min*
Affiliation:
Centre for Experimental & Constructive Mathematics Department of Mathematics and Statistics Simon Fraser University Burnaby, BC V5A 1S6, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper considers the rational system 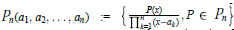${{P}_{n}}({{a}_{1}},{{a}_{2}},...,{{a}_{n}})\,\,:=\,\left\{ \frac{P(x)}{\Pi _{k=1}^{n}(x-{{a}_{k}})},\,P\,\in \,{{P}_{n}} \right\}$ with nonreal elements in 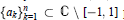$\left\{ {{a}_{k}} \right\}_{k=1}^{n}\,\subset \,\mathbb{C}\,\backslash \,[-1,\,1]$ paired by complex conjugation. It gives a sharp (to constant) Markov-type inequality for real rational functions in 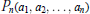${{P}_{n}}({{a}_{1}},{{a}_{2}},...,{{a}_{n}})$. The corresponding Markov-type inequality for high derivatives is established, as well as Nikolskii-type inequalities. Some sharp Markov- and Bernstein-type inequalities with curved majorants for rational functions in 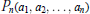${{P}_{n}}({{a}_{1}},{{a}_{2}},...,{{a}_{n}})$ are obtained, which generalize some results for the classical polynomials. A sharp Schur-type inequality is also proved and plays a key role in the proofs of our main results

Keywords

41A1726D0726C15Markov-type inequalityBernstein-type inequalityNikolskii-type inequalitySchur-type inequalityrational functions with prescribed polescurved majorantsChebyshev polynomials
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 1 , 01 February 1998 , pp. 152 - 166
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Achiezer, N.I., Theory of Approximation.Ungar, New York, 1956.Google Scholar
2. Borwein, P., Inequalities and inverse theorems in restricted rational approximation theory. Canad. J. Math. 32 (1980), 345–361.Google Scholar
3. Borwein, P. and Erdélyi, T., Polynomials and Polynomial Inequalities.Springer, New York, 1995.Google Scholar
4. Borwein, P. , Sharp extensions of Bernstein's inequality to rational spaces. Mathematica 43 (1996), 413–423.Google Scholar
5. Borwein, P., Erdélyi, T. and Zhang, J., Chebyshev polynomials and Markov-Bernstein type inequalities for the rational spaces. J. London Math. Soc. 50 (1994), 501–519.Google Scholar
6. Cheney, E.W., Introduction to Approximation Theory.McGraw-Hill, New York, 1966.Google Scholar
7. Lachance, M.A., Bernstein and Markov inequalities for constrained polynomials. Rational Approximation and Interpolation, 125–135. Lecture Notes in Math. 1045 , Springer-Verlag, 1984.Google Scholar
8. Li, X., Mohapatra, R.N. and Rodriguez, R.S., Bernstein-type inequalities for rational functions with prescribed poles. J. London Math. Soc. 51 (1995), 523–531.Google Scholar
9. Lorentz, G.G., Approximation of Functions.Holt Rinehart and Winston, New York, 1966.Google Scholar
10. Milovanovi, G.V.ć, Mitrinovi, D.S.ć and Th. M. Rassias, Topics in Polynomials: Extremal Problems, Inequalities, Zeros. World Scientific, Singapore, 1994.Google Scholar
11. Natanson, I.P., Constructive Function Theory. Vol I, Ungar, New York, 1964.Google Scholar
12. Petrushev, P. and Popov, V.A., Rational Approximation of Real Functions. Cambridge Univ. Press, 1987.Google Scholar
13. Rahman, Q.I., On a problem of Turán about polynomials with curved majorants. Trans. Amer. Math. Soc. 163 (1972), 447–455.Google Scholar
14. Rahman, Q.I. and Schmeisser, G., Les Inégalités de Markoff et de Bernstein. Les Presses de L’Université de Montreal, 1983.Google Scholar
15. Rivlin, T.J., Chebyshev Polynomials.second edition, John Wiley & Sons, 1990.Google Scholar