No CrossRef data available.
Published online by Cambridge University Press: 06 February 2025
Given a full right-Hilbert 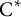 $\mathrm {C}^{*}$-module
$\mathrm {C}^{*}$-module 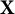 $\mathbf {X}$ over a
$\mathbf {X}$ over a 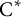 $\mathrm {C}^{*}$-algebra A, the set
$\mathrm {C}^{*}$-algebra A, the set 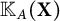 $\mathbb {K}_{A}(\mathbf {X})$ of A-compact operators on
$\mathbb {K}_{A}(\mathbf {X})$ of A-compact operators on 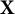 $\mathbf {X}$ is the (up to isomorphism) unique
$\mathbf {X}$ is the (up to isomorphism) unique 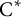 $\mathrm {C}^{*}$-algebra that is strongly Morita equivalent to the coefficient algebra A via
$\mathrm {C}^{*}$-algebra that is strongly Morita equivalent to the coefficient algebra A via 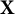 $\mathbf {X}$. As a bimodule,
$\mathbf {X}$. As a bimodule, 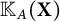 $\mathbb {K}_{A}(\mathbf {X})$ can also be thought of as the balanced tensor product
$\mathbb {K}_{A}(\mathbf {X})$ can also be thought of as the balanced tensor product 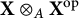 $\mathbf {X}\otimes _{A} \mathbf {X}^{\mathrm {op}}$, and so the latter naturally becomes a
$\mathbf {X}\otimes _{A} \mathbf {X}^{\mathrm {op}}$, and so the latter naturally becomes a 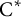 $\mathrm {C}^{*}$-algebra. We generalize both of these facts to the world of Fell bundles over groupoids: Suppose
$\mathrm {C}^{*}$-algebra. We generalize both of these facts to the world of Fell bundles over groupoids: Suppose 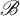 $\mathscr {B}$ is a Fell bundle over a groupoid
$\mathscr {B}$ is a Fell bundle over a groupoid 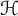 $\mathcal {H}$ and
$\mathcal {H}$ and 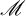 $\mathscr {M}$ is an upper semi-continuous Banach bundle over a principal
$\mathscr {M}$ is an upper semi-continuous Banach bundle over a principal 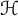 $\mathcal {H}$-space X. If
$\mathcal {H}$-space X. If 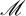 $\mathscr {M}$ carries a right-action of
$\mathscr {M}$ carries a right-action of 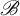 $\mathscr {B}$ and a sufficiently nice
$\mathscr {B}$ and a sufficiently nice 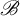 $\mathscr {B}$-valued inner product, then its imprimitivity Fell bundle
$\mathscr {B}$-valued inner product, then its imprimitivity Fell bundle 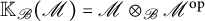 $\mathbb {K}_{\mathscr {B}}(\mathscr {M})=\mathscr {M}\otimes _{\mathscr {B}} \mathscr {M}^{\mathrm {op}}$ is a Fell bundle over the imprimitivity groupoid of X, and it is the unique Fell bundle that is equivalent to
$\mathbb {K}_{\mathscr {B}}(\mathscr {M})=\mathscr {M}\otimes _{\mathscr {B}} \mathscr {M}^{\mathrm {op}}$ is a Fell bundle over the imprimitivity groupoid of X, and it is the unique Fell bundle that is equivalent to 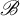 $\mathscr {B}$ via
$\mathscr {B}$ via 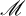 $\mathscr {M}$. We show that
$\mathscr {M}$. We show that 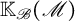 $\mathbb {K}_{\mathscr {B}}(\mathscr {M})$ generalizes the “higher order” compact operators of Abadie–Ferraro in the case of saturated bundles over groups, and that the theorem recovers results such as Kumjian’s Stabilization trick.
$\mathbb {K}_{\mathscr {B}}(\mathscr {M})$ generalizes the “higher order” compact operators of Abadie–Ferraro in the case of saturated bundles over groups, and that the theorem recovers results such as Kumjian’s Stabilization trick.
The work was supported by Methusalem grant METH/21/03 — long term structural funding of the Flemish Government, and an FWO Senior Postdoctoral Fellowship (project number 1206124N).