Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:57:19.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic Functionals on Open Riemann Surfaces

Published online by Cambridge University Press:  20 November 2018

P. M. Gauthier  and
L. A. Rubel
P. M. Gauthier
Affiliation:
Université de Montréal, Montréal, Québec
L. A. Rubel
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 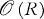denote the space of functions holomorphic on an open Riemann surface R, where 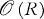has the topology of uniform convergence on compact sets. In this note, we characterize the dual space 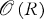*. The result is not new, for it is implicitly contained in the more general results of Tillmann [5] and, in case R is planar, in those of Köthe [4]. However, the paper of Gunning and Narasimhan [3], which appeared subsequently, allows us to give a short proof of this important result. Actually, our characterization is a natural one in terms of differentials, while the Köthe-Tillmann characterization is in terms of functions, but we show that these two characterizations are isomorphic. We end our paper by using our characterization to prove an interpolation result. The second author gratefully acknowledges a helpful discussion with Professor George Szekeres.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 4 , 01 August 1976 , pp. 885 - 888
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Behnke, H. and Stein, K., Entwicklungen analytischer Funktionen auf Riemannschen Fldchen, Math. Ann. 120 (1949), 430–461.Google Scholar
2. Gauthier, P. M. and Rubel, L. A., Interpolation in separable Fréchet spaces with applications to spaces of analytic functions, Can. J. Math. 27 (1975), 1110–1113.Google Scholar
3. Gunning, R. C. and Narasimhan, R., Immersion of open Riemann surfaces, Math. Ann. 174 (1967), 103–108.Google Scholar
4. Kôthe, G., Dualitdt in der Funktionentheorie, J. reine u. angew. Math. 191 (1953), 30–49.Google Scholar
5. Tillmann, H. G., Dualitdt in der Funktionentheorie auf Riemannschen Fldchen, J. reine u. angew. Math. 105 (1956), 76–101.Google Scholar