Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T19:22:02.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Hodge Theory of Cyclic Covers Branchedover a Union of Hyperplanes

Published online by Cambridge University Press:  20 November 2018

Donu Arapura
Donu Arapura*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, U.S.A.. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that $Y$ is a cyclic cover of projective space branched over a hyperplane arrangement 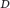$D$ and that 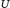$U$ is the complement of the ramification locus in $Y$. The first theorem in this paper implies that the Beilinson–Hodge conjecture holds for 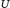$U$ if certain multiplicities of 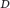$D$ are coprime to the degree of the cover. For instance, this applies when 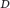$D$ is reduced with normal crossings. The second theorem shows that when 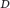$D$ has normal crossings and the degree of the cover is a prime number, the generalized Hodge conjecture holds for any toroidal resolution of $Y$. The last section contains some partial extensions to more general nonabelian covers.

Keywords

14C30Hodge cycleshyperplane arrangements
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 3 , 01 June 2014 , pp. 505 - 524
Copyright
Copyright © Canadian Mathematical Society 2014

References

[AS] Asakura, M. and Saito, S., Noether-Lefschetz locus for Beilinson–Hodge cycles. I. Math. Z. 252(2006), no. 2, 251–273. http://dx.doi.org/10.1007/s00209-005-0813-x Google Scholar
[A] Arapura, D., Varieties with very little transcendental cohomology. In: Motives and algebraic cycles, Fields Inst. Commun., 56, American Mathematical Society, Providence, RI, 2009, pp. 1–14.Google Scholar
[AK] Arapura, D. and Kumar, M., Beilinson–Hodge cycles on semiabelian varieties. Math. Res. Lett. 16(2009), no. 4, 557–562. http://dx.doi.org/10.4310/MRL.2009.v16.n4.a1 Google Scholar
[Ba] Bailey, W. L., On the imbedding of V-manifolds in projective space. Amer. J. Math. 79(1957), 403–430. http://dx.doi.org/10.2307/2372689 Google Scholar
[B] Beilinson, A., Notes on absolute Hodge cohomology. In: Applications of algebraic K-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., 55, American Mathematical Society, Providence, RI, 1986.Google Scholar
[Br] Brieskorn, E., Sur les groupes de tresses (d’après V. I. Arnold). Séminaire Bourbaki, Lecture Notes in Math., 317, Springer, Berlin, 1973, pp. 21–44.Google Scholar
[BS] Budur, N. and Saito, M., Jumping coefficients and spectrum of a hyperplane arrangement. Math. Ann. 347(2010), no. 3, 545–579. http://dx.doi.org/10.1007/s00208-009-0449-y Google Scholar
[C] Chatzistamatiou, A., On the Beilinson–Hodge conjecture for H2 and rational varieties. Math. Res. Lett. 19(2012), no. 1, 149–164. http://dx.doi.org/10.4310/MRL.2012.v19.n1.a12 Google Scholar
[CLS] Cox, D., Little, J., and Schenck, H. K., Toric varieties. Graduate Studies in Mathematics, 124, American Mathematical Society, Providence, RI, 2011.Google Scholar
[CR] Curtis, C.W. and Reiner, I., Representation theory of finite groups and associative algebras. Reprint of the 1962 original.Wiley Classics Library. AWiley-Interscience Publication. JohnWiley & Sons, Inc., New York, 1988.Google Scholar
[DP] De Concini, C. and Procesi, C., Wonderful models of subspace arrangements. Selecta Math. 1(1995), no. 3, 459–494. http://dx.doi.org/10.1007/BF01589496 Google Scholar
[D1] Deligne, P., Équations différentielles à points singuliers réguliers. Lecture Notes in Mathematics, 163, Springer-Verlag, Berlin-New York, 1970.Google Scholar
[D2] Deligne, P., Théorie de Hodge II. Inst. Hautes Études Sci. Publ. Math. 40(1971), 5–57.Google Scholar
[D3] Deligne, P., Théorie de Hodge III. Inst. Hautes Études Sci. Publ. Math. 44(1974), 5–77.Google Scholar
[EV1] Esnault, H. and Viehweg, E., Logarithmic De Rham complexes and vanishing theorems. Invent Math 86(1986), no. 1, 161–194. http://dx.doi.org/10.1007/BF01391499Google Scholar
[EV2] Esnault, H., Lectures on vanishing theorems. DMV Seminar, 20, Birkhäuser Verlag, Basel, 1992Google Scholar
[G] Grothendieck, A., Hodge's general conjecture is false for trivial reasons. Topology 8(1969), 299–303. http://dx.doi.org/10.1016/0040-9383(69)90016-0 Google Scholar
[H] Hirzebruch, F., Topological methods in algebraic geometry. Reprint of the 1978 ed., Classics in Mathematics, Springer-Verlag, Berlin, 1995.Google Scholar
[J] Jannsen, U., Mixed motives and algebraic K-theory. Lecture Notes in Mathematics, 1400, Springer-Verlag, Berlin, 1990.Google Scholar
[M] Kempf, G., Knudsen, F., Mumford, D., and Saint-Donat, B., Toroidal embeddings. I. Lecture Notes in Mathematics, 339, Springer-Verlag, Berlin-New York, 1973.Google Scholar
[N] Nori, M. V., Algebraic cycles and Hodge theoretic connectivity. Invent. Math. 111(1993), no. 2, 349–373. http://dx.doi.org/10.1007/BF01231292 Google Scholar
[R] Rota, G.-C., On the foundations of combinatorial theory. I. Theory of Mäbius functions. Z.Wahrscheinlichkeitstheorie und Verw. Gebiete 2(1964), 340–368. http://dx.doi.org/10.1007/BF00531932 Google Scholar
[S] Shioda, T., On the Picard number of a complex projective variety. Ann. Sci. École Norm. Sup. (4) 14(1981), no. 3, 303–321.Google Scholar
[St] Steenbrink, J. H. M., Mixed Hodge structures on vanishing cohomology. In: Real and complex singularities (Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976), Sijthoff and Noordhoff, Alphen aan den Rijn, 1977, pp. 525–563.Google Scholar
[T] Timmerscheid, K.t, Mixed Hodge theory for unitary local systems. J. Reine Angew. Math. 379(1987), 152–171. http://dx.doi.org/10.1515/crll.1987.379.152. Google Scholar
[V] Voisin, C., Hodge theory and complex algebraic geometry. II. Cambridge Studies in Advanced Mathematics, 77, Cambridge University Press, Cambridge, 2003.Google Scholar