Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:43:16.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Derivations and Distinguished Subfields

Published online by Cambridge University Press:  20 November 2018

James K. Deveney  and
Nickolas Heerema
James K. Deveney
Affiliation:
Virginia Commonwealth University, Richmond, Virginia
Nickolas Heerema
Affiliation:
Florida State University, Tallahassee, Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L be a finitely generated extension of a field K having characteristic p ≠ 0. A rank t higher derivation on L over K is a sequence

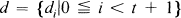
of additive maps of K into K such that

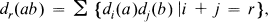
d0 is the identity map and dt(x) = 0, i > 0, x ∊ K. [6] contains the relevant background material on higher derivations. By Zorn's Lemma, there are maximal separable extensions of K in L. A maximal separable extension D of K in L is called distinguished if

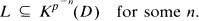
Dieudonné [4] established that any finitely generated extension always has distinguished subfields. L has the same dimension over any distinguished subfield [5], and this dimension is called the order of inseparability of L/K. The least n such that K(LP)n is separable over K is called the inseparable exponent of L/K, inex(L/K).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 1 , 01 February 1988 , pp. 131 - 141
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Deveney, J. and Mordeson, J., Subfields and invariants of inseparable field extensions, Can. J. Math.. 29 (1977), 1304–1311.Google Scholar
2. Deveney, J. and Mordeson, J., Calculating invariants of inseparable extensions, P.A.M.S.. 81 (1981), 373–376.Google Scholar
3. Deveney, J. and Mordeson, J., The order of inseparability of fields, Can. J. Math.. 31 (1979), 655–662.Google Scholar
4. Dieudonné, J., Sur les extensions transcendantes, Summa Brasil. Math. 2 (1947), 1–20.Google Scholar
5. Heerema, N., Higher derivation Galois theory of fields, TAMS. 265 (1981), 169–179.Google Scholar
6. Heerema, N. and Deveney, J., Galois theory for fields K/k finitely generated, TAMS. 189 (1974), 263–274.Google Scholar
7. Heerema, N. and Tucker, D., Modular field extensions, P.A.M.S.. 53 (1975), 306–306.Google Scholar
8. Kreimer, H. F. and Heerema, N., Modularity and separability for field extensions, Can. J. Math.. 27 (1975), 1176–1182.Google Scholar
9. Jacobson, N., Lectures in abstract algebra, Vol III: Theory of fields and Galois theory (Van Nostrand, Princeton N.J., 1964).CrossRefGoogle Scholar
10. Kraft, H., Inseparable Korpererweiterungen, Comment. Math. Helv. 45 (1970), 110–118.Google Scholar
11. Mordeson, J., On a Galois theory for inseparable field extensions, T.A.M.S.. 214 (1975), 337–347.Google Scholar
12. Mordeson, J., Splitting of field extensions, Arch. Math. (Basel). 26 (1975), 606–610.Google Scholar
13. Tucker, D., Finitely generated field extensions, Dissertation, Florida State University, Tallahassee, Florida (1975).Google Scholar
14. Waterhouse, W., The structure of inseparable field extensions, T.A.M.S.. 211 (1975), 39–56.Google Scholar