Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T10:35:06.573Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic Mappings of Negatively Curved Manifolds

Published online by Cambridge University Press:  20 November 2018

Zvi Har'el
Zvi Har'el*
Affiliation:
Technion, Israel Institute of Technology, Haifa 32000, Israel; University of Illinois at Urbana-Champaign, Urbana, Illinois 61801
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Volume decreasing properties of harmonic mappings of space forms were investigated by S. S. Chern and S. I. Goldberg [3] and the author. In a previous paper [6], a step toward generalization of the results was made proving the following theorem:

Theorem. Let ƒ: M —> N be a harmonic mapping of n-dimensional Riemannian manifolds, with C ≦ 0. Suppose the scalar curvature of M is not less than — S, and the Ricci curvature of N is not greater than —S/n, where S ≧ 0 and S > 0 are constants. Then, if u has a maximum on M,

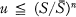
i.e. ƒ is volume decreasing up to a constant.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 3 , 01 June 1978 , pp. 631 - 637
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Aubin, T., Fonction de Green et valeurs propres du laplacien, J. Math, pures et appl. 53 (1974), 347–371.Google Scholar
2. Bishop, R. L. and O'Neill, B., Manifolds of negative curvature, Trans. Amer. Math. Soc. 145 (1969), 1–49.Google Scholar
3. Chern, S. S. and Goldberg, S. I., On the volume decreasing property of a class of real harmonic mappings, Amer. J. Math., 97 (1975), 133–147.Google Scholar
4. Goldberg, S. I., Curvature and homology (Second printing, Academic Press, New York, 1962).Google Scholar
5. Goldberg, S. I., On the distance decreasing property of a class of real harmonic mappings, Geometriae Dedicata, 4 (1975), 61–69.Google Scholar
6. Har'El, Z., Harmonic mappings and distortion theorems, Tensor (N.S.) 30 (1976), 47–54.Google Scholar
7. Har'El, Z., Harmonic mappings and distortion theorems, D.Sc. thesis, Technion-Israel Institute of Technology, Haifa, June 1975.Google Scholar
8. Yau, S. T., A general Schwarz lemma for Hermitian manifolds, to appear, Amer. J. Math.Google Scholar