Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T06:00:33.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Gorenstein Witt Rings

Published online by Cambridge University Press:  20 November 2018

Robert W. Fitzgerald
Robert W. Fitzgerald*
Affiliation:
Southern Illinois University, Carbondale, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout R is a noetherian Witt ring. The basic example is the Witt ring WF of a field F of characteristic not 2 and 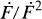finite. We study the structure of (noetherian) Witt rings which are also Gorenstein rings (i.e., have a finite injective resolution). The underlying motivation is the elementary type conjecture. The Gorenstein Witt rings of elementary type are group ring extensions of Witt rings of local type. We thus wish to compare the two classes of Witt rings: Gorenstein and group ring over local type. We show the two classes enjoy many of the same properties and are, in several cases, equal. However we cannot decide if the two classes are always equal.

In the first section we consider formally real Witt rings R (equivalently, dim R = 1). Here the total quotient ring of R is R-injective if and only if R is reduced. Further, R is Gorenstein if and only if R is a group ring over Z. This result appears to be somewhat deep.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1186 - 1202
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bass, H. On the ubiquity of Gorenstein rings, Math. Z. 82 (1963), 8–28.Google Scholar
2. Cordes, C. and Ramsey, J., Quadratic forms over quadratic extensions of fields with two quaternion algebras, Can J. Math. 31 (1979), 1047–1058.Google Scholar
3. Eilenberg, S. and T. Nakayama, On the dimension of modules and algebras, II, Nagoya Math. J. 9 (1955), 1–16.Google Scholar
4. Elman, R., Lam, T. Y. and Wadsworth, A., Pfister ideals in Witt rings, Math. Ann. 245 (1979), 219–245.Google Scholar
5. Faith, C., Algebra: rings, modules and categories, II, Grundlehren Math. Wiss. 191, (Springer-Verlag, New York/Heidelberg/Berlin, 1976).Google Scholar
6. Fitzgerald, R., Primary ideals in Witt rings, J. Alg. 96 (1985), 368–385.Google Scholar
7. Fitzgerald, R., Ideal class groups of Witt rings, To appear in J. Alg.Google Scholar
8. Fitzgerald, R. and Yucas, J., Combinatorial techniques and finitely generated Witt rings, I, J. Alg. 774 (1988), 40–52.Google Scholar
9. Kaplansky, I., Commutative rings (University of Chicago Press, Chicago/London, 1974).Google Scholar
10. Lam, T. Y., The algebraic theory of quadratic forms (Benjamin, Reading, Mass., 1973).Google Scholar
11. Marshall, M., Abstract Witt rings, Queen's Papers in Pure and Applied Mathematics, 57 Kingston, Ont. (1980).Google Scholar
12. Szymiczek, K., Generalized Hilbert fields, J. Reine Angew. Math. 329 (1981), 58–65.Google Scholar
13. Ware, R., When are Witt rings group rings? Pac. J. Math. 49 (1973), 279–284.Google Scholar
14. Zariski, O. and Samuel, P., Commutative algebra, I, GTM 28 (Springer-Verlag, New York/Heidelberg/Berlin, 1975).Google Scholar