No CrossRef data available.
Published online by Cambridge University Press: 20 November 2024
In this paper, we prove the global exstence of weak solutions for a porous medium dynamics of m species moving between two domains separated by a zero-thickness membrane. On this membrane, Kedem–Katchalsky conditions are considered, and the study is characterized by natural structural conditions applied to the nonlinear reactive terms. The global existence is established under the assumption that these reactive terms are bounded in 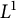 $L^1$. This problem has already been analyzed in the linear diffusion case by Ciavolella and Perthame in Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540). The present work constitutes an extension for nonlinear diffusion, particularly of the porous medium type, in the form
$L^1$. This problem has already been analyzed in the linear diffusion case by Ciavolella and Perthame in Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540). The present work constitutes an extension for nonlinear diffusion, particularly of the porous medium type, in the form 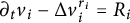 $\partial _t v_i - \Delta v_i^{r_i} = R_i$, for an exponent
$\partial _t v_i - \Delta v_i^{r_i} = R_i$, for an exponent 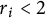 $r_i < 2$. The case
$r_i < 2$. The case 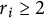 $r_i \geq 2$ remains an open problem. This paper is an adaptation of the ideas from Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540), with new strategies to overcome the appearance of nonlinearity and degeneracy in the diffusion term.
$r_i \geq 2$ remains an open problem. This paper is an adaptation of the ideas from Ciavolella and Perthame (2021, Journal of Evolution Equations 21, 1513–1540), with new strategies to overcome the appearance of nonlinearity and degeneracy in the diffusion term.