Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rooney, P. G.
1969.
Abstract Spaces and Approximation / Abstrakte Räume und Approximation.
Vol. 10,
Issue. ,
p.
258.
Benedetto, J. J.
and
Heinig, H. P.
1983.
Harmonic Analysis.
Vol. 992,
Issue. ,
p.
240.


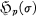 , σ real, 1 ≤
, σ real, 1 ≤