Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T17:32:38.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Gamma Factors, Root Numbers, and Distinction

Published online by Cambridge University Press:  20 November 2018

Nadir Matringe  and
Omer Offen
Nadir Matringe
Affiliation:
Laboratoire de Mathématiques et Applications Téléport 2 - BP 30179, 11 Boulevard Marie et Pierre Curie, 86962 Futuroscope Chasseneuil Cedex, France email: [email protected]
Omer Offen
Affiliation:
Department of Mathematics, Technion, Israel Institute of Technology, Haifa 3200003, Israel email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a relation between distinction and special values of local invariants for representations of the general linear group over a quadratic extension of 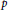$p$-adic fields. We show that the local Rankin–Selberg root number of any pair of distinguished representation is trivial, and as a corollary we obtain an analogue for the global root number of any pair of distinguished cuspidal representations. We further study the extent to which the gamma factor at 1/2 is trivial for distinguished representations as well as the converse problem.

Keywords

11F70distinguished representationlocal constant
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 3 , 01 June 2018 , pp. 683 - 701
Copyright
Copyright © Canadian Mathematical Society 2018

References

[AnaO8] Anandavardhanan, U. K., Root numbers of Asai L-functions. Int. Math. Res. Not. IMRN 2008, Art. ID rnnl25. http://dx.doi.org/10.1093/imrn/rnn125 Google Scholar
[AKT04] Anandavardhanan, U. K., Kable, A. C., and Tandon, R., Distinguished representations and poles of twisted tensor L-functions. Proc. Amer. Math. Soc. 132(2004), no. 10, 2875–2883. http://dx.doi.org/10.1090/S0002-9939-04-07424-6 Google Scholar
[AM17] Anandavardhanan, U. K. and Matringe, N., Test vectors for local periods. Forum Math., to appear. http://dx.doi.Org/10.1515/forum-2016-0169 Google Scholar
[AR05] Anandavardhanan, U. K. and Rajan, C. S., Distinguished representations, base change, and reducibility for unitary groups. Int. Math. Res. Not. 2005, no. 14, 841–854. http://dx.doi.org/10.1155/IMRN.2005.841 Google Scholar
[Che06] Chen, J. P. J., The n x (n – 2) local converse theorem for GL(n) over a p-adic field. J. Number Theory 120(2006), no. 2, 193–205. http://dx.doi.Org/10.1016/j.jnt.2005.12.001 Google Scholar
[Fli91] Flicker, Y. Z., On distinguished representations. J. Reine Angew. Math. 418(1991), 139–172. http://dx.doi.Org/10.1515/crll.1991.418.139 Google Scholar
[GK75] Gel'fand, I. M. and Kajdan, D. A., Representations of the group GL(n, K) where K is a local field. In: Lie groups and their representations (Proc. Summer School, Bolyai János Math. Soc, Budapest, 1971), Halsted, New York, 1975, pp. 95–118.Google Scholar
[Gurl5] Gurevich, M., On a local conjecture of Jacquet, ladder representations and standard modules. Math. Z. 281(2015), no. 3-4, 1111–1127. http://dx.doi.org/10.1007/s00209-015-1522-8 Google Scholar
[Hak91] Hakim, J., Distinguished p-adic representations. Duke Math. J. 62(1991), no. 1, 1–22. http://dx.doi.Org/10.1215/S0012-7094-91-06201-0 Google Scholar
[HO15] Hakim, J. and Offen, O., Distinguished representations of GL(n) and local converse theorems. ManuscriptaMath. 148(2015), no. 1-2, 1–27. http://dx.doi.Org/10.1007/s00229-015-0740-z Google Scholar
[Hen93] Henniart, G., Caractérisation de la correspondance de Langlands locale par lesfacteurs ε de paires. Invent. Math. 113(1993), no. 2, 339–350. http://dx.doi.Org/10.1007/BF01244309 Google Scholar
[JL15] Jacquet, H. and Liu, B., On the local converse theorem for p-adic gln. arxiv:1 601.03656Google Scholar
[JNS15] Jiang, D., Nien, C., and Stevens, S., Towards the Jacquet conjecture on the local converse problem for p-adic GLn . J. Eur. Math. Soc. (JEMS) 17(2015), no. 4, 991–1007. http://dx.doi.org/10.4171/JEMS/524 Google Scholar
[JPSS83] Jacquet, H., Piatetskii-Shapiro, I. I., and Shalika, J. A., Rankin-Selberg convolutions. Amer. J. Math. 105(1983), no. 2, 367–464. http://dx.doi.org/10.2307/2374264 Google Scholar
[JS85] Jacquet, H. and Shalika, J., A lemma on highly ramified e-factors. Math. Ann. 271(1985), no. 3, 319–332. http://dx.doi.org/10.1007/BF01456070 Google Scholar
[KabO4] Kable, A. C., Asai L-functions and facquet's conjecture. Amer. J. Math. 126(2004), no. 4, 789–820. http://dx.doi.org/10.1353/ajm.2004.0030 Google Scholar
[Keml5] Kemarsky, A., Gamma factors of distinguished representations of GLn(ℂ). Pacific J. Math. 278(2015), no. 1, 137–172. http://dx.doi.org/10.2140/pjm.2015.278.137 Google Scholar
[Mat09a] Matringe, N., Conjectures about distinction and local Asai L-functions. Int. Math. Res. Not. IMRN 2009, no. 9, 1699–1741. http://dx.doi.Org/10.1093/imrn/rnp002 Google Scholar
[Mat09b] Matringe, N., Distinguished principal series representation of GL(n) over a p-adic field. Pacific J. Math. 239(2009), no. 1, 53–63. http://dx.doi.org/10.2140/pjm.2009.239.53 Google Scholar
[Off11] Offen, O., On local root numbers and distinction. J. Reine Angew. Math. 652(2011), 165–205. http://dx.doi.Org/10.1515/CRELLE.2011.017 Google Scholar
[Ok97] Ok, Y., Distinction and gamma factors at 1/2: Supercuspidal case. Ph.D. Thesis, Columbia University, 1997.Google Scholar
[Sha85] Shahidi, F., Local coefficients as Artin factors for real groups. Duke Math. J. 52(1985), no. 4, 973–1007. http://dx.doi.Org/10.1215/S0012-7094-85-05252-4 Google Scholar
[Sil78] Silberger, A. J., The Langlands quotient theorem for p-adic groups. Math. Ann. 236(1978), no. 2, 95–104. http://dx.doi.org/10.1007/BF01351383 Google Scholar
[Wal92] Wallach, N. R., Real reductive groups. II. Pure and Applied Mathematics, 132, Academic Press Inc., Boston, MA, 1992.Google Scholar
[Zel80] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. Ecole Norm. Sup. (4) 13(1980), no. 2, 165–210. http://dx.doi.Org/10.24033/asens.1379 Google Scholar