Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:07:51.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Fuchsian Subgroups of the Picard Group

Published online by Cambridge University Press:  20 November 2018

Benjamin Fine
Benjamin Fine*
Affiliation:
Fairfield University, Fairfield, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Picard group Γ = PSL2 (Z(i)) is the group of linear transformations

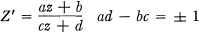with a, b, c, d Gaussian integers.

Γ is of interest both as an abstract group and in automorphic function theory [10]. In [10] Waldinger constructed a subgroup H of finite index which is a generalized free product, while in [1] Fine showed that T is a semidirect product with the subgroup H, contained as a subgroup of finite index in the normal factor.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 3 , 01 June 1976 , pp. 481 - 485
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Fine, B., The structure of PSL2﹛A), Annals of Mathematics Study 79 (1974).Google Scholar
2. Fine, B. and Marvin Tretkoff, The SQ-universality of certain arithmetically defined groups, to appear, J. London Math. Soc.Google Scholar
3. Karrass, A. and Solitar, D., Subgroups of infinite index in Fuchsian groups, Math. Z. 125 (1972), 59–69.Google Scholar
4. to appear.Google Scholar
5. Lehner, J., Discontinuous groups and automorphic functions, Math. Surveys No. 8, Amer. Math. Soc. (Providence, R.I. 1964).Google Scholar
6. Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Interscience, Wiley, New York, 1966).Google Scholar
7. Maskit, B., On a class of Kleinian groups, American Academy of Science Fenn. Ser. AI 1+1+2 (1969).Google Scholar
8. Mennicke, J., A note on regular coverings of closed orientable surfaces, Proc. Glasgow Math. Assoc. 5 (1969), 49–66.Google Scholar
9. Sansone, G., sotto gruppe del gruppo di Picard e due teoremi sui gruppi finiti analoghi at teorema del dyck, Rend. Circ. Mat. Palermo 1+7 (1923), 273.Google Scholar
10. Waldinger, H., On the subgroups of the Picard group, Proc. Amer. Math. Soc. 16 (1965), 1373–1378.Google Scholar