Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T05:15:27.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Clones Containing All Permutations

Published online by Cambridge University Press:  20 November 2018

L. Haddad  and
I. G. Rosenberg
L. Haddad
Affiliation:
Department of Mathematics and Computer Science RMC Kingston, Ontario K7K5L0
I. G. Rosenberg
Affiliation:
Mathématiqués et Statistics, Université de Montréal C.R 6128 Succ., Centre-ville Montréal, Québec H3C 3J7
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a finite set with |A| > 2. We describe all clones on A containing the set SA of all permutations of A among its unary operations. (A clone on A is a composition closed set of finitary operations on A containing all projections). With a few exceptions such a clone C is either essentially unary or cellular i.e. there exists a monoid M of self-maps of A containing SA such that either C = 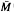(= all essentially unary operations agreeing with some f ∊ M) or C = 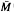∪ Гh where 1 < h ≤ |A| and Гh consists of all finitary operations on A taking at most h values. The exceptions are subclones of Burle's clone or of its variant (provided |A| is even).

Keywords

08A0508A4008A02
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 5 , 01 October 1994 , pp. 951 - 970
Copyright
Copyright © Canadian Mathematical Society 1994

References

[Be-McK 84] Berman, J. and McKenzie, R., Clones satisfying the term condition, Discrete Math. 52(1984), 7–29.Google Scholar
[Bu 67] Burle, G. A., Classes of k-valued logic which contain all functions of a single variable, (Russian), Diskret. Analic (Novosibirsk) 10(1967), 3–7.Google Scholar
[But 60] Butler, J. W., On complete and independent sets of operations in finite algebras, Pacific J. Math. 10(1960), 1169–1179.Google Scholar
[Cs 83] Csákány, B., All minimal clones on the three-element set, Acta Cybernet 6(1983), 227–238.Google Scholar
[Da-Ro 85] Davies, R. O. and Rosenberg, I. G., Precomplete classes of operations on an uncountable set, Colloq. Math. (1)50(1985), 1–12.Google Scholar
[Ga 59] Gavrilov, G. P., On some completeness conditions in countably-valued logics, (Russian), Dokl. Akad. Nauk SSSR 128(1959), 21–24.Google Scholar
[Ga 64] Gavrilov, G. P., On quasi-Peano functions, (Russian), Dokl. Akad. Nauk SSSR 156(1964), 1011–1013; English translation, Soviet Math. Dokl. 156(1964), 750–752.Google Scholar
[Ga 64a] Gavrilov, G. P., The power of sets of closed classes of finite height in , (Russian), Dokl. Akad. Nauk SSSR 158(1964), 503–506; English translation, Soviet Math. Dokl. 158(1964), 1239–1242.Google Scholar
[Ga 65] Gavrilov, G. P., On functional completeness in countably valued logic, (Russian), Problemi Tekhn. Kibernet. Robot. 15(1965), 5–65.Google Scholar
[Ha-Ro 86] Haddad, L. and Rosenberg, I. G., An interval of finite clones isomorphic to (P(N),⊆), C. R. Math. Rep. Acad. Sci. Canada (6) 8(1986), 375–379.Google Scholar
[Ha-Ro 88] Haddad, L. and Rosenberg, I. G., Familles larges de clones sur un ensemble fini, Ann. Sci. Math. Québec (1) 12(1988), 55–72.Google Scholar
[Ha-Ro 88a] Haddad, L. and Rosenberg, I. G., Un intervalle booléen de clones sur un univers fini, Ann. Sci. Math. Québec (2) 12(1988), 211–232.Google Scholar
[Ho-McK 88] Hobby, D. and McKenzie, R., The structure of finite algebras (Tame congruence theory), Contemp. Math. 18(1988).Google Scholar
[Ja 58] Jablonskii, S. V., Functional constructions in a k-valued logic, (Russian), Trudy Mat. Inst. Steklov. 51(1958), 5–142.Google Scholar
[Ja-Mu 59] Janov, Ju. I. and Mucnik, A. A., On the existence of k-valued closed classes that have no bases, (Russian), Dokl. Akad. Nasuk SSSR 127(1959), 44–46.Google Scholar
[La 82] Lau, D., Die Maximalen Klassen von Polk(0), (German), Rostock. Math. Kolloq. 19(1982), 229–47.Google Scholar
[La 82a] Lau, D., Submaximale klassen von P3 , Elektron. Inform. Kybernet. (4-5) 18(1982), 227–243.Google Scholar
[Ma A 66] Mal'tsev, A. I., Iterative algebras and Post's varieties, (Russian), Algebra i Logika (2) 5(1966), 5–24; English translation, The Met. of Algebraic System, Collected papers 1936-67, Studies in Logics and Foundations of Math. 66, North-Holland, 1971.Google Scholar
[Ma A 67] Mal'tsev, A. I., A strengthening of the theorems ofSlupecki and Iablonskii, (Russian, English Summary), Algebra i Logika (3) 6(1967), 61–75.Google Scholar
[Ma I 73] Mal'tsev, A. I., Certain properties of cells of Post algebras, (Russian), Metody Diskret. Analiz 23(1973), 24–31.Google Scholar
[Pa 84] P. P. Pálfy, , Unary polynomials in algebras I, Algebra Universalis 18(1984), 262–273.Google Scholar
[Po 41] Post, E., The two-valued iterative systems of mathematical logic, Ann. Math. Studies 5, Princeton Univiversity Press, 1941.Google Scholar
[Ro 65] Rosenberg, I. G., La structure des fonctions de plusieurs variables sur un ensemble fini, C. R. Acad. Sci. Paris Sér. 260(1965), 3817–3819.Google Scholar
[Ro 70] Rosenberg, I. G., Über die funktionale Vollständigkeit in den mehrwertigen Logiken, (German), Rozpravy Československé Akad. Věd Řada Mat. Přírod. Věd 80(1970), 3–93.Google Scholar
[Ro 70a] Rosenberg, I. G., Complete sets for finite algebras, Math. Nachr. (1-6) 44(1970), 225–258.Google Scholar
[Ro 77] Rosenberg, I. G., On closed classes, basic sets and groups, Proc. VII-th it Internat. Sympos. Multiple-valued Logic, Charlotte, North Carolina, 1977, 1–6.Google Scholar
[Ro78] Rosenberg, I. G., Ramifications ofSlupecki's lemma, Proceedings of 24th Conference of the History of Logic, Cracow, 1978, 58–74.Google Scholar
[Sa 60] Salomaa, A., On the composition of functions of several variables ranging over a finite set, Ann. Univ. Turku. Ser. A 41(1960), 7–47.Google Scholar
[Sa 60a] Salomaa, A., A theorem concerning the composition of functions of several variables ranging over a finite set, J. Symbolic Logic (3) 25(1960), 203–208.Google Scholar
[Sa 62] Salomaa, A., Some completeness criteria for sets of functions over a finite domain, Ann. Univ. Turku. Ser. A 53(1962), 3–9.Google Scholar
[SI 39] Slupecki, J., Completeness criterion for systems of many-valued propositional logics, (Polish), C. R. Séances Soc. Sci. Lettres Varsovie Cl. III 32(1939), 102–109, English Translation, Studia Logica 30(1972), 153–157.Google Scholar