Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Louboutin, Stéphane
2003.
Explicit Lower bounds for residues at 𝑠=1 of Dedekind zeta functions and relative class numbers of CM-fields.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 8,
p.
3079.
Louboutin, Stéphane R.
2004.
Algorithmic Number Theory.
Vol. 3076,
Issue. ,
p.
318.
Park, Sun-Mi
Yang, Hee-Sun
and
Kwon, Soun-Hi
2007.
The class number one problem for the normal CM-fields of degree 32.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 10,
p.
5057.
Louboutin, Stéphane R.
2007.
Some explicit upper bounds for residues of zeta functions of number fields taking into account the behavior of the prime 2.
manuscripta mathematica,
Vol. 125,
Issue. 1,
p.
43.
Park, Sun-Mi
and
Kwon, Soun-Hi
2007.
Class number one problem for normal CM-fields.
Journal of Number Theory,
Vol. 125,
Issue. 1,
p.
59.
Li, Xiannan
2012.
The smallest prime that does not split completely in a number field.
Algebra & Number Theory,
Vol. 6,
Issue. 6,
p.
1061.
Cho, Peter J.
and
Kim, Henry H.
2013.
Probabilistic properties of number fields.
Journal of Number Theory,
Vol. 133,
Issue. 12,
p.
4175.
CLARK, PETE L.
COOK, BRIAN
and
STANKEWICZ, JAMES
2013.
TORSION POINTS ON ELLIPTIC CURVES WITH COMPLEX MULTIPLICATION (WITH AN APPENDIX BY ALEX RICE).
International Journal of Number Theory,
Vol. 09,
Issue. 02,
p.
447.
Hambleton, Samuel A.
and
Williams, Hugh C.
2018.
Cubic Fields with Geometry.
p.
63.
Cho, Peter J.
and
Kim, Henry H.
2018.
Moments of logarithmic derivatives of L-functions.
Journal of Number Theory,
Vol. 183,
Issue. ,
p.
40.
Lumley, Allysa
2018.
Explicit bounds for L-functions on the edge of the critical strip.
Journal of Number Theory,
Vol. 188,
Issue. ,
p.
186.
Debaene, Korneel
2019.
Explicit counting of ideals and a Brun–Titchmarsh inequality for the Chebotarev density theorem.
International Journal of Number Theory,
Vol. 15,
Issue. 05,
p.
883.
Dixit, Anup B
2021.
On the Generalized Brauer–Siegel Theorem for Asymptotically Exact Families of Number Fields with Solvable Galois Closure.
International Mathematics Research Notices,
Vol. 2021,
Issue. 14,
p.
10941.
WONG, PENG-JIE
2022.
ON STARK’S CLASS NUMBER CONJECTURE AND THE GENERALISED BRAUER–SIEGEL CONJECTURE.
Bulletin of the Australian Mathematical Society,
Vol. 106,
Issue. 2,
p.
288.
Lowry-Duda, David
Taniguchi, Takashi
and
Thorne, Frank
2022.
Uniform bounds for lattice point counting and partial sums of zeta functions.
Mathematische Zeitschrift,
Vol. 300,
Issue. 3,
p.
2571.
Mine, Masahiro
2023.
The value-distribution of artin L-functions associated with cubic fields in conductor aspect.
Mathematische Zeitschrift,
Vol. 304,
Issue. 4,
Koymans, Peter
and
Pagano, Carlo
2023.
On Malle’s conjecture for nilpotent groups.
Transactions of the American Mathematical Society, Series B,
Vol. 10,
Issue. 11,
p.
310.
Bordellès, Olivier
2023.
From the Ideal Theorem to the class number.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 4,
p.
1368.
McGown, Kevin J.
and
Tucker, Amanda
2024.
An improved error term for counting D4$D_4$‐quartic fields.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 9,
p.
2874.
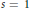 $s=1$ of
$s=1$ of  $L$-series associated with primitive characters on ray class groups of number fields. To make it quite clear to the reader how useful such bounds are when dealing with class number problems for CM-fields, we deduce an upper bound for the root discriminants of the normal CM-fields with (relative) class number one.
$L$-series associated with primitive characters on ray class groups of number fields. To make it quite clear to the reader how useful such bounds are when dealing with class number problems for CM-fields, we deduce an upper bound for the root discriminants of the normal CM-fields with (relative) class number one.

