Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T17:44:10.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions of Arbitrary Analytic Functions in Series of Exponentials

Published online by Cambridge University Press:  20 November 2018

D. G. Dickson
D. G. Dickson*
Affiliation:
University of Michigan, Ann Arbor, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ϕ ≠ 0 be an entire function of one complex variable and of exponential type. Let B denote the set of all monomial exponentials of the form zneζ where ζ is a zero of ϕ of order greater than h. If R is a simply connected plane region and H(R) denotes the space of functions analytic in R with the topology of uniform convergence on compacta, then ϕ can be considered as an element of the topological dual H′(R) if the Borel transform 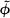of ϕ is analytic on 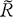, the complement of R. The duality is given by

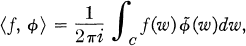
where C is a simple closed curve in the common region of analyticity of ƒ and 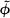, and C winds once around the complement of a set in which 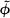is analytic.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 2 , 01 April 1981 , pp. 347 - 356
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Dickson, D. G., Expansions in series of solutions of linear difference-differential and infinité order differential equations with constant coefficients, Mem. Amer. Math. Soc. 23 (1957), 860.Google Scholar
2. Dickson, D. G., Analytic mean periodic functions, Trans. Amer. Math. Soc. 110 (1964), 361–374.Google Scholar
3. Dzjadyk, V. K., On convergence conditions for Dirichlet series on closed polygons, Mat. Sb. 95(173) (1974), 475–493.Google Scholar
4. Dzjadyk, V. K. and Krutigolova, E. K., The representation of analytic functions by a Dirichlet series at the boundary of the convergence domain, Mat. Zametki 14 (1973), 796–780.Google Scholar
5. Krutigolova, E. K., The behavior of a Dirichlet series on the boundary of a region of convergence, Ukrain. Mat. Z. 27 (1975), 234–240.Google Scholar
6. Krutigolova, E. K., Representation of analytic functions by Dirichlet series on the boundaries of closed convex polygon domains, Ukrain. Mat. Z. 27 (1975), 516–521.Google Scholar
7. Leont'ev, A. F., Representation of arbitrary functions by Dirichlet series, Dokl. Nauk SSSR 164 (1965), 40–42.Google Scholar
8. Leont'ev, A. F., On the representation of functions by sequences of Dirichlet polynomials, Mat. Sb. 70 (112) (1966), 132–144.Google Scholar
9. Leont'ev, A. F., Qn jfoe representation of analytic functions by Dirichlet series, Mat. Sb. 80 (122) (1969), 117–156.Google Scholar
10. Leont'ev, A. F., Representation of functions by generalized Dirichlet series, Uspehi Mat. Nauk 4 (1969), 97–164.Google Scholar
11. Leont'ev, A. F., On conditions of expandibility of analytic functions in Dirichlet series, Izv. Akad. Nauk SSSR 36 (1972), 1282–1295.Google Scholar
12. Leont'ev, A. F., On the representation of analytic functions in a closed convex region by a Dirichlet series, Izv. Akad. Nauk SSSR Ser. Mat. 37 (1973), 577–592.Google Scholar
13. Leont'ev, A. F., The representation of analytic functions in a polygonal convex closed domain by Dirichlet series, Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 127–137.Google Scholar
14. Moore, M. G., On expansions in series of exponential functions, Amer. J. Math. 62 (1940), 83–90.Google Scholar
15. Sedletskii, A. M., Expansions of functions into Dirichlet series on closed convex polygons, Siberian Math. J. 19 (1979), 622–629.Google Scholar