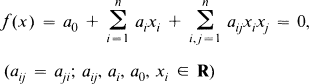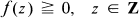Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Erdahl, Robert
1992.
A cone of inhomogeneous second-order polynomials.
Discrete & Computational Geometry,
Vol. 8,
Issue. 4,
p.
387.
Deza, M.
Grishukhin, V. P.
and
Laurent, M.
1993.
The hypermetric cone is polyhedral.
Combinatorica,
Vol. 13,
Issue. 4,
p.
397.
Deza, Michel
and
Laurent, Monique
1994.
Applications of cut polyhedra — II.
Journal of Computational and Applied Mathematics,
Vol. 55,
Issue. 2,
p.
217.
Deza, M.
and
Onn, S.
1995.
Lattice-free polytopes and their diameter.
Discrete & Computational Geometry,
Vol. 13,
Issue. 1,
p.
59.
Alexeev, Valery
and
Nakamura, Iku
1999.
On Mumford's construction of degenerating abelian varieties.
Tohoku Mathematical Journal,
Vol. 51,
Issue. 3,
Барановский, Евгений П
Baranovskii, Evgenii P
Кононенко, Павел Геннадьевич
and
Kononenko, Pavel Gennadyevich
2000.
Об одном способе вывода $L$-многогранников $n$-мерных решеток.
Математические заметки,
Vol. 68,
Issue. 6,
p.
830.
Кононенко, Павел Геннадьевич
and
Kononenko, Pavel Gennadyevich
2002.
Аффинные типы $L$-многогранников 5-мерных решеток.
Математические заметки,
Vol. 71,
Issue. 3,
p.
412.
Deza, Michel
and
Dutour, Mathieu
2003.
The Hypermetric Cone on Seven Vertices.
Experimental Mathematics,
Vol. 12,
Issue. 4,
p.
433.
Grishukhin, Viacheslav
2019.
Uniquely scaled dual cells.
European Journal of Combinatorics,
Vol. 80,
Issue. ,
p.
151.
Agostini, Daniele
Fevola, Claudia
Mandelshtam, Yelena
and
Sturmfels, Bernd
2023.
KP solitons from tropical limits.
Journal of Symbolic Computation,
Vol. 114,
Issue. ,
p.
282.