Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:49:39.190Z Has data issue: false hasContentIssue false
  • English
  • Français

The Empty Sphere Part II

Published online by Cambridge University Press:  20 November 2018

S. S. Ryshkov  and
R. M. Erdahl
S. S. Ryshkov
Affiliation:
Steklov Institute, Moscow, USSR
R. M. Erdahl
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Blow up a sphere in one of the interstices of a lattice until it is held rigidly. There will be no lattice points in the interior and sufficiently many on the boundary so that their convex hull is a solid figure. Such a sphere was called an empty sphere by B. N. Delone in 1924 when he introduced his method for lattice coverings [3, 4]. The circumscribed polytope is called an L-polytope. Our interest in such matters stems from the following result [6, Theorems 2.1 and 2.3]: With a list of the L-polytopes for lattices of dimension ≦n one can give a geometrical description of the possible sets of integer solutions of

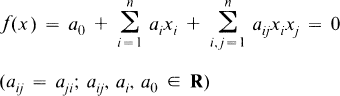
where f satisfies the following condition (in which Z denotes the integers):

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1058 - 1073
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Coxeter, H. S. M., Regular poly topes (Dover, New York, 1973).Google Scholar
2. Coxeter, H. S. M., Regular and semi-regular poly topes. II, Mat. Z. 188 (1986), 559–591.Google Scholar
3. Delaunay, B., Sur la sphere vide, Proc. Internat. Congr. Math. I (Univ. of Toronto Press, Toronto, 1928), 695–700.Google Scholar
4. Delone, B. N., The geometry of positive quadratic forms, Uspehi Mat. Nauk 3, (1937) 16–62; 4, (1938) 102–164, (Russian).Google Scholar
5. Erdahl, R. M., A cone of inhomogeneous second order polynomials, to appear.Google Scholar
6. Erdahl, R. M. and Ryshkov, S. S., The empty sphere, Can. J. Math. 39 (1987), 794–824.Google Scholar
7. Ryshkov, S. S. and Erdahl, R. M., The geometry of the integer roots of some quadraticequations with many variables, Soviet Math. Dokl. 26 (1982).Google Scholar
8. Ryshkov, S. S. and Baranovskii, E. P., Classical methods in the theory of lattice packings, Uspehi Mat. Nauk 34 (1979); English transi, in Russian Math. Surveys 34 (1979).Google Scholar
9. Ryshkov, S. S. and Baranovskii, E. P., The C-types of n-dimensional lattices and the five-dimensional primitive par allelohedrons (with applications to the theory of covering), Trudy Mat. Inst. Steklov 137 (1976); Engl, transi. Proc. Steklov Inst. Mat. 137 (1976).Google Scholar
10. Ryshkov, S. S. and Šušbaev, S. Š., The structure of the L-partition for the second perfect lattice, Mat. Sbornik 116 (1981); English transi, in Math. USSR Sbornik 44 (1983).Google Scholar
11. Vornoi, G. F., Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire, J. Reine Angew. Math. 133 (1908), 79–178.Google Scholar
12. Vornoi, G. F., Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire, J. Reine Angew. Math. 134 (1908), 198–287; 136 (1909), 67–178.Google Scholar