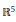Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Riveros, Carlos
Rodrigues, Luciana
and
Tenenblat, Keti
2008.
On Dupin hypersurfaces with constant Möbius curvature.
Pacific Journal of Mathematics,
Vol. 236,
Issue. 1,
p.
89.
Riveros, Carlos M. C.
2010.
Dupin hypersurfaces with four principal curvatures in ℝ5 with principal coordinates.
Revista Matemática Complutense,
Vol. 23,
Issue. 2,
p.
341.
Riveros, Carlos M.C.
and
Corro, Armando M.V.
2012.
CLASSES OF HYPERSURFACES WITH VANISHING LAPLACE INVARIANTS.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 4,
p.
685.
Ferro, Marcelo Lopes
Rodrigues, Luciana Ávila
and
Tenenblat, Keti
2014.
On a class of Dupin hypersurfaces in $$R^5$$ with nonconstant Lie curvature.
Geometriae Dedicata,
Vol. 169,
Issue. 1,
p.
301.
Cecil, Thomas E.
and
Ryan, Patrick J.
2015.
Geometry of Hypersurfaces.
p.
233.
Ferro, Marcelo Lopes
Rodrigues, Luciana Ávila
and
Tenenblat, Keti
2016.
On Dupin Hypersurfaces in R 5 Parametrized by Lines of Curvature.
Results in Mathematics,
Vol. 70,
Issue. 3-4,
p.
499.
Li, Tongzhu
Qing, Jie
and
Wang, Changping
2017.
Möbius curvature, Laguerre curvature and Dupin hypersurface.
Advances in Mathematics,
Vol. 311,
Issue. ,
p.
249.
Cezana, Miguel
and
Tenenblat, Keti
2017.
Dupin hypersurfaces with constant Laguerre curvatures.
manuscripta mathematica,
Vol. 154,
Issue. 1-2,
p.
169.