Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T14:40:08.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersed Factorization Structures

Published online by Cambridge University Press:  20 November 2018

H. Herrlich ,
G. Salicrup  and
R. Vazquez
H. Herrlich
Affiliation:
Universitdt Bremen, Achterstrasse, BRD
G. Salicrup
Affiliation:
Institute de Matheméticas U.N.A.M., Mexico
R. Vazquez
Affiliation:
Institute de Matheméticas U.N.A.M., Mexico
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

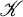Factorization structures on a category form a useful categorical tool. As is known, any 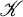, satisfying suitable completeness—and smallness—conditions, has a sufficient supply of factorization structures; in fact, there is a bijection between the class of all epireflective (full and isomorphism- closed) subcategories of 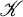and the class of all so called perfect factorizationstructures of 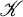In this paper, for an arbitrary category 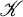supplied with a fixed factorization structure (E, M), a similar bijection between the class of all E-reflective (full and isomorphism-closed) subcategories of 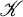and the class of all (E, M)-dispersed factorization structures on 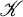, introduced in this paper, will be established.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 5 , 01 October 1979 , pp. 1059 - 1071
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Adâmek, J., Herrlich, H. and Strecker, G. E., Least and largest initial completions, Preprint.Google Scholar
2. Collins, P. J., Concordant mappings and the concordant dissonant factorization of an arbitrary continuous function, Proc. Amer. Math. Soc. 27 (1971), 587–591.Google Scholar
3. Collins, P. J. and Dyckhoff, R., Connection properties and factorization theorems, Preprint.Google Scholar
4. Dyckhoff, R., Factorization theorems and projective spaces in topology, Math. Zeitschrif. 127 (1972), 256–264.Google Scholar
5. Dyckhoff, R., Perfect light maps and inverse limits, Quart. J. Math. Oxfor. 25 (1974), 441–449.Google Scholar
6. Dyckhoff, R., Categorical cuts, Gen. Topology and Appl. 6 (1976), 291–295.Google Scholar
7. Dyckhoff, R., Categorical methods in dimension theory, Proc. First Categorical Topology Symposium, Lecture Notes in Math. 540 (Springer, Berlin, 1976), 220–242.Google Scholar
8. Herrlich, H., A generalization of perfect maps, Proc. Third Prague Topological Symposium, General Topology and Its Relations to Modern Analysis and Algebra III (Academia, Prague, 1972), 187–191.Google Scholar
9. Herrlich, H., Perfect subcategories and factorizations, Proc. Colloq. Karzthely, Topics in Topology, Colloq. Math. Soc. Janos Bolyai 8 (North Holland, Amsterdam, 1974), 387–403.Google Scholar
10. Herrlich, H., Topological functors, Gen. Topology and Appl. 4 (1974), 125–142.Google Scholar
11. Herrlich, H. and Strecker, G. E., Semi-universal maps and universal initial completions, Preprint.Google Scholar
12. Kannan, V. and Rajagopalan, M., Constructions and applications of rigid spaces I, Advances in Math. 29 (1978).Google Scholar
13. Nakagawa, R., Relations between two reflections, Sci. Rep. Tokyo Kyoiku Daigaku Sect.. A12 (1973), 80–88.Google Scholar
14. Nel, L. D., Development classes: an approach to perfectness, reflectiveness and extension problems, Proc. Second Pittsburgh Internat. Conf. TOPO 72—General Topology and its Applications, Lecture Notes in Math. 378 (Springer, Berlin, 1974), 322–340.Google Scholar
15. Preuss, G., Relative connectednesses and disconnectednesses in topological categories, Quaestiones Matematica. 2 (1977), 297–306.Google Scholar
16. Preuss, G., On factorization of maps in topological categories, Preprint.Google Scholar
17. Pumpliin, D., Kategorien, Unpublished notes, University of Munster, (1974).Google Scholar
18. Salicrup, G. and Vazquez, R., Categorias de conexion, An. Inst. Mat. Univ. Nac. Autônoma Mexic. 12 (1972), 47–87.Google Scholar
19. Salicrup, G. and Vazquez, R., Reflexividad y cononexidad en Top, An. Inst. Mat. Univ. Nac. Autônoma Mexic. 14 (1974), 159–230.Google Scholar
20. Salicrup, G. and Vazquez, R., Reflectivity and connectivity in topological categories, Preprint.Google Scholar
21. Strecker, G. E., Epireflection operators vs. perfect morphisms and closed classes of epimorphisms, Bull. Austral. Math. Soc. 7 (1972), 359–366.Google Scholar
22. Strecker, G. E., On characterizations of perfect morphisms and epireflective hulls, Proc. Second Pittsburgh Internat. Conf, TOPO 72. General Topology and its Applications, Lecture Notes in Math. 378 (Springer, Berlin, 1974), 468–500.Google Scholar
23. Strecker, G. E., Component properties and factorizations, Topological Structures, Math. Centre Tract. 52 (1974), 123–140.Google Scholar
24. Strecker, G. E., Perfect sources, Proc. First Categorical Topology Symposium, Lecture Notes in Math. 540 (Springer, Berlin, 1976), 605–624.Google Scholar
25. Tholen, W., Semi-topological functors I, Preprint.Google Scholar
26. Trnkovâ, V., Non-constant continuous mappings of metric or compact Hausdorff spaces, Comment. Math. Univ. Carolina. 13 (1972), 283–295.Google Scholar