Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:16:20.211Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dichromate and Orientations of a Graph

Published online by Cambridge University Press:  20 November 2018

Gerald Berman
Gerald Berman*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Internal and external activities are defined for any orientation of a graph relative to a fixed labelling of its edges. It is shown that the number of such orientations of having internal activity r and external activity s is 2r+sXrs where Xrs is the coefficient of xrys in the dichromate It follows that the number of orientations of in which the resulting digraph is acyclic is given by 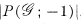, where is the chromatic polynomial associated with .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 5 , 01 October 1977 , pp. 947 - 956
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Berge, Claude, Graphs and hypergraphs (North Holland, Amsterdam, 1973).Google Scholar
2. Biggs, Norman, Algebraic graph theory (Cambridge U. Press, London, 1974).Google Scholar
3. Harary, F. and Palmer, E., On the number of orientations of a given graph, Bull, de L'Acad. Polonaise des Sciences 14 (1966), 125–128.Google Scholar
4. Minty, G. J., Monotone networks, Proc. Roy. Soc. A257(1960), 194–208.Google Scholar
5. Stanley, R. P., Acyclic orientations of graphs, Discrete Math. 5 (1973), 171–178.Google Scholar
6. Tutte, V. T., A contribution to the theory of chromatic polynomials, Can. J. Math. 6 (1953), 80–91.Google Scholar
7. Tutte, V. T. A class of abelian groups, Can. J. Math. 8 (1956), 13–28.Google Scholar
8. Tutte, V. T. On dichromatic polynomials, J. Comb. Theory 2 (1967), 301–320.Google Scholar
9. Tutte, V. T. The dichromatic polynomial, Proc. Fifth British Combinatorial Conference, University of Aberdeen (1975), 605–635.Google Scholar