Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berrick, A. J.
Karoubi, M.
and
Østvær, P. A.
2011.
Periodicity of hermitianK-groups.
Journal of K-theory,
Vol. 7,
Issue. 3,
p.
429.
Jardine, J. F.
2023.
Victor Percy Snaith, 1944–2021.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
1041.
Tachikawa, Yuji
Yamashita, Mayuko
and
Yonekura, Kazuya
2025.
Remarks on Mod-2 Elliptic Genus.
Communications in Mathematical Physics,
Vol. 406,
Issue. 1,



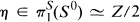 generate the stable one-stem. Then there are weak equivalences of spectra
generate the stable one-stem. Then there are weak equivalences of spectra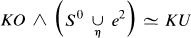
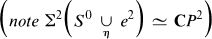 and
and
