No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In this paper, we study the Mordell-Weil group of an elliptic curve as a Galois module. We consider an elliptic curve 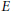 $E$ defined over a number field
$E$ defined over a number field  $K$ whose Mordell-Weil rank over a Galois extension
$K$ whose Mordell-Weil rank over a Galois extension  $F$ is 1, 2 or 3. We show that
$F$ is 1, 2 or 3. We show that 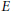 $E$ acquires a point (points) of infinite order over a field whose Galois group is one of
$E$ acquires a point (points) of infinite order over a field whose Galois group is one of
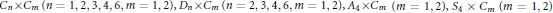 ${{C}_{n}}\times {{C}_{m}}(n=1,\,2,\,3,\,4,\,6,\,m\,=\,1,\,2),\,{{D}_{n}}\times {{C}_{m}}(n=2,\,3,\,4,\,6,\,m=\,1,\,2),\,{{A}_{4}}\times {{C}_{m}}(m=1,\,2),\,{{S}_{4}}\,\times \,{{C}_{m}}(m=1,\,2)$
. Next, we consider the case where
${{C}_{n}}\times {{C}_{m}}(n=1,\,2,\,3,\,4,\,6,\,m\,=\,1,\,2),\,{{D}_{n}}\times {{C}_{m}}(n=2,\,3,\,4,\,6,\,m=\,1,\,2),\,{{A}_{4}}\times {{C}_{m}}(m=1,\,2),\,{{S}_{4}}\,\times \,{{C}_{m}}(m=1,\,2)$
. Next, we consider the case where 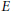 $E$ has complex multiplication by the ring of integers
$E$ has complex multiplication by the ring of integers 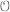 $\mathcal{O}$ of an imaginary quadratic field
$\mathcal{O}$ of an imaginary quadratic field 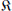 $\Re $ contained in
$\Re $ contained in  $K$. Suppose that the
$K$. Suppose that the 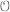 $\mathcal{O}$-rank over a Galois extension
$\mathcal{O}$-rank over a Galois extension  $F$ is 1 or 2. If
$F$ is 1 or 2. If 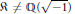 $\Re \ne \mathbb{Q}(\sqrt{-1})$ and
$\Re \ne \mathbb{Q}(\sqrt{-1})$ and 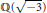 $\mathbb{Q}(\sqrt{-3})$ and
$\mathbb{Q}(\sqrt{-3})$ and 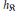 ${{h}_{\Re }}$ (class number of
${{h}_{\Re }}$ (class number of 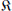 $\Re $) is odd, we show that
$\Re $) is odd, we show that 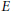 $E$ acquires positive
$E$ acquires positive 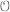 $\mathcal{O}$-rank over a cyclic extension of
$\mathcal{O}$-rank over a cyclic extension of  $K$ or over a field whose Galois group is one of
$K$ or over a field whose Galois group is one of
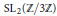 $\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$
, an extension of
$\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$
, an extension of
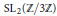 $\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$
by
$\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$
by 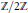 $\mathbb{Z}/2\mathbb{Z}$, or a central extension by the dihedral group. Finally, we discuss the relation of the above results to the vanishing of
$\mathbb{Z}/2\mathbb{Z}$, or a central extension by the dihedral group. Finally, we discuss the relation of the above results to the vanishing of 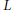 $L$-functions.
$L$-functions.