Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T13:05:22.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Cumulants of the q-semicircular Law, Tutte Polynomials, and Heaps

Published online by Cambridge University Press:  20 November 2018

Matthieu Josuat-Vergès
Matthieu Josuat-Vergès*
Affiliation:
CNRS and Institut Gaspard Monge, Université Paris-Est Marne-la-Vallée, 5 Boulevard Descartes, Champssur- Marne, 77454 Marne-la-Vallée cedex 2, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 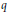$q$-semicircular distribution is a probability law that interpolates between the Gaussian law and the semicircular law. There is a combinatorial interpretation of its moments in terms of matchings, where 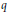$q$ follows the number of crossings, whereas for the free cumulants one has to restrict the enumeration to connected matchings. The purpose of this article is to describe combinatorial properties of the classical cumulants. We show that like the free cumulants, they are obtained by an enumeration of connected matchings, the weight being now an evaluation of the Tutte polynomial of a so-called crossing graph. The case 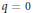$q=0$ of these cumulants was studied by Lassalle using symmetric functions and hypergeometric series. We show that the underlying combinatorics is explained through the theory of heaps, which is Viennot's geometric interpretation of the Cartier–Foata monoid. This method also gives a general formula for the cumulants in terms of free cumulants.

Keywords

05A1805C3146L54momentscumulantsmatchingsTutte polynomialsheaps
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 863 - 878
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Aigner, M., A course in enumeration. Graduate Texts in Mathematics, 238, Springer, Berlin, 2007.Google Scholar
[2] Amdeberhan, T., Moll, V. H., and Vignat, C., A new proof of a conjecture by D. Zeilberger about Catalan numbers. arxiv:1202.1203v1 Google Scholar
[3] Anshelevich, M., Belinschi, S. T., Bozejko, M., and Lehner, F., Free infinite divisibility for q- Gaussians. Math. Res. Lett. 17(2010), no. 5, 905–916.Google Scholar
[4] Belinschi, S., Bozejko, M., Lehner, F., and Speicher, R., The normal distribution is ⊞-infinitely divisible. Adv. Math. 226(2011), no. 4, 3677–3698. http://dx.doi.org/10.1016/j.aim.2010.10.025 Google Scholar
[5] Blitvić, N., On the norm of q-circular operators. arxiv:1102.0748 Google Scholar
[6] Bousquet-Mélou, M. and Viennot, X. G., Empilements de segments et q-énumération de polyominos convexes dirigés. J. Combin. Theory Ser. A 60(1992), no. 2, 196–224. http://dx.doi.org/10.1016/0097-3165(92)90004-E Google Scholar
[7] Bozejko, M., Kümmerer, B., and Speicher, R., q-Gaussian processes: non-commutative and classical aspects. Comm. Math. Phys. 185(1997), no. 1, 129–154. http://dx.doi.org/10.1007/s002200050084 Google Scholar
[8] Bozejko, M. and Speicher, R., An example of a generalized brownian motion. Comm. Math. Phys. 137(1991), no. 3, 519–531. http://dx.doi.org/10.1007/BF02100275 Google Scholar
[9] Burman, Y. and Shapiro, B., Around matrix-tree theorem. Math. Res. Lett. 13(2006), no. 5–6, 761–774.Google Scholar
[10] Cartier, P. and Foata, D., Problémes combinatoires de commutation et réarrangements. Lecture Notes in Mathematics, 85, Springer-Verlag, Berlin-New York, 1969.Google Scholar
[11] Fédou, J.-M., Sur les fonctions de Bessel. Discrete Math. 139(1995), no. 1–3, 473–480. http://dx.doi.org/10.1016/0012-365X(94)00150-H Google Scholar
[12] Fédou, J.-M., Combinatorial objects enumerated by q-Bessel functions. Rep. Math. Phys. 34(1994), no. 1, 57–70. dx.doi.org/10.1016/0034-4877(94)90017-5 Google Scholar
[13] Gioan, E., Enumerating degree sequences in digraphs and a cycle-cocycle reversing system. European J. Combin. 28(2007), no. 4, 1351–1366. http://dx.doi.org/10.1016/j.ejc.2005.11.006 Google Scholar
[13] Gioan, E., Enumerating degree sequences in digraphs and a cycle-cocycle reversing system. European J. Combin. 28(2007), no. 4, 1351–1366. http://dx.doi.org/10.1016/j.ejc.2005.11.006 Google Scholar
[14] Greene, C. and Zaslavsky, T., On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non-Radon partitions, and orientations of graphs. Trans. Amer. Math. Soc. 280(1983), no. 1, 97–126. http://dx.doi.org/10.1090/S0002-9947-1983-0712251-1 Google Scholar
[15] Hiai, F. and Petz, D., The semicircle law, free random variables and entropy. Mathematical Surveys and Monographs, 77, American Mathematical Society, Providence, RI, 2000.Google Scholar
[16] Ismail, M. E. H., Stanton, D., and Viennot, G., The combinatorics of q-Hermite polynomials and the Askey-Wilson integral. European J. Combin. 8(1987), no. 4, 379–392.Google Scholar
[17] Lassalle, M., Two integer sequences related to Catalan numbers. J. Combin. Theory Ser. A 119(2012), no. 4, 923–935. http://dx.doi.org/10.1016/j.jcta.2012.01.002 Google Scholar
[18] Lehner, F., Free cumulants and enumeration of connected partitions. European J. Combin. 23(2002), no. 8, 1025–1031. http://dx.doi.org/10.1006/eujc.2002.0619 Google Scholar
[19] Nica, A. and Speicher, R., Lectures on the combinatorics of free probability. London Mathematical Society Lecture Note Series, 335, Cambridge University Press, Cambridge, 2006.Google Scholar
[20] Sokal, A. D., The multivariate Tutte polynomial (alias Potts model) for graphs and matroids. In: Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327, Cambridge University Press, Cambridge, 2005, pp. 173–226.Google Scholar
[21] Stanley, R. P., Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, Cambridge, 1999.Google Scholar
[22] Szegö, G., Ein Beitrag zur Theorie der Thetafunktionen. Sitz. Preuss. Akad.Wiss. Phys. Math. Kl. 19(1926), 242–252.Google Scholar
[23] Touchard, J., Sur un problème de configurations et sur les fractions continues. Canad. J. Math. 4(1952), 2–25. http://dx.doi.org/10.4153/CJM-1952-001-8 Google Scholar
[24] van Leeuwen, H. and Maassen, H., A q-deformation of the Gauss distribution. J. Math. Phys. 36(1995), no. 9, 4743–4756. http://dx.doi.org/10.1063/1.530917 Google Scholar
[25] van Leeuwen, H., An obstruction for q-deformation of the convolution product. J. Phys. A 29(1996), no. 15, 4741–4748. http://dx.doi.org/10.1088/0305-4470/29/15/036 Google Scholar
[26] Viennot, G. X., Heaps of pieces. I. Basic definitions and combinatorial lemmas. In: Combinatoire énumérative (Montreal, Que., 1985) Lecture Notes in Math., 1234, Springer, Berlin, 1986, pp. 321–350.Google Scholar