Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T05:14:29.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Cubic Base Change for 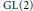$\text{GL(2)}$

Published online by Cambridge University Press:  20 November 2018

Zhengyu Mao  and
Stephen Rallis
Zhengyu Mao
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, USA and Department of Mathematics, and Computer Science, Rutgers University at Newark, Newark, NJ 07102, USA email: [email protected]
Stephen Rallis
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a relative trace formula that establishes the cubic base change for 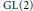$\text{GL(2)}$. One also gets a classification of the image of base change. The case when the field extension is nonnormal gives an example where a trace formula is used to prove lifting which is not endoscopic.

Keywords

11F7011F72
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 1 , 01 February 2000 , pp. 172 - 196
Copyright
Copyright © Canadian Mathematical Society 2000

References

[A] Arthur, J., A trace formula for reductive groups I. Duke Math J. 45 (1978), 911–952.Google Scholar
[G-R-S] Ginzburg, D., Rallis, S. and Soudry, D., Cubic correspondence arising from G2. Amer. J. Math. (2) 119 (1997), 251–335.Google Scholar
[J] Jacquet, H., The continuous spectrum of the relative trace formula for GL(3) over a quadratic extension. Israel J. Math 89 (1995), 1–59.Google Scholar
[J1] Jacquet, H., On the nonvanishing of some L-functions. Proc. Indian. Acad. Sci. 97 (1987), 117–155.Google Scholar
[J2] Jacquet, H., Local theory for GL(2): matching conditions. Notes.Google Scholar
[J-Lai] Jacquet, H. and Lai, K., A relative trace formula. Comp. Math. 54 (1985), 243–310.Google Scholar
[J-PS-S] Jacquet, H., Piatetski-Shapiro, I. and Shalika, J., Relèvement cubique non normal. C. R. Acad. Sci. Paris 292 (1981), 567–571.Google Scholar
[J-Y] Jacquet, H. and Ye, Y., Une remarque sur le changement de base quadratique. C. R. Acad. Sci. Paris 311 (1990), 671–676.Google Scholar
[J-Y2] Jacquet, H. and Ye, Y., Distinguished representations and quadratic base change for GL(3). Trans. Amer. Math. Soc. 348 (1996), 913–939.Google Scholar
[K] Kazhdan, D., The minimal representation of D4. Prog. Math. 92 (1990), 125–158.Google Scholar
[La] Labesse, L., L-indistinguishable representations and the trace formula for SL(2). In: Lie groups and their representations, John Wiley, 1975.Google Scholar
[L] Langlands, R., Base change for GL(2). Ann. of Math. Stud. 96 (1980), Princeton University Press.Google Scholar
[M-R] Mao, Z. and Rallis, S., On a cubic lifting. Israel J. Math., to appear.Google Scholar
[M-R1] Mao, Z. and Rallis, S., A trace formula for dual pairs. Duke J. Math. (2) 87 (1997), 321–341.Google Scholar
[M-R2] Mao, Z. and Rallis, S., Howe duality and trace formula. Pacific J. Math., to appear.Google Scholar
[Se] Serre, J-P., A course in arithmetic. Graduate Texts in Math. 7 (1973), Springer-Verlag.Google Scholar
[T] Tunnell, J., Artin's conjecture for representations of octahedral type. Bull. Amer. Math. Soc. (2) 5 (1981), 173–175.Google Scholar
[W] Weil, A., Sur certains groupes d’opérateurs unitaires. Acta Math. 111 (1964), 143–211.Google Scholar
[W1] Weil, A., Adeles and algebraic groups. Prog. Math. 23 , Birkh¨auser, Boston, 1982.Google Scholar
[Wi] Wiles, A., Modular elliptic curves and Fermat's Last Theorem. Ann. of Math. 142 (1995), 443–551.Google Scholar