Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-05-02T10:03:57.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Cross-sectional C*-algebras associated with subgroups

Part of: Selfadjoint operator algebras Locally compact groups and their algebras

Published online by Cambridge University Press:  19 December 2024

Damián Ferraro Open the ORCID record for Damián Ferraro [Opens in a new window]
Damián Ferraro*
Affiliation:
Departamento de Matemática y Estadística del Litoral, CENUR Litoral Norte, Universidad de la República, Salto, Uruguay
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Fell bundle 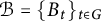$\mathcal {B}=\{B_t\}_{t\in G}$ over a locally compact group G and a closed subgroup 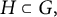$H\subset G,$ we construct quotients 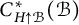$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$ and 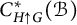$C^{*}_{H\uparrow G}(\mathcal {B})$ of the full cross-sectional C*-algebra 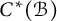$C^{*}(\mathcal {B})$ analogous to Exel–Ng’s reduced algebras 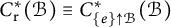$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\equiv C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})$ and 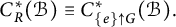$C^{*}_R(\mathcal {B})\equiv C^{*}_{\{e\}\uparrow G}(\mathcal {B}).$ An absorption principle, similar to Fell’s one, is used to give conditions on 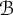$\mathcal {B}$ and H (e.g., G discrete and 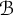$\mathcal {B}$ saturated, or H normal) ensuring 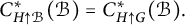$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{H\uparrow G}(\mathcal {B}).$ The tools developed here enable us to show that if the normalizer of H is open in G and 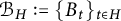$\mathcal {B}_H:=\{B_t\}_{t\in H}$ is the reduction of 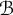$\mathcal {B}$ to 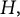$H,$ then 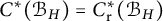$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$ if and only if 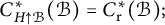$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B});$ the last identification being implied by $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$ We also prove that if G is inner amenable and 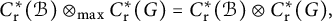$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G)=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B})\otimes C^{*}_{\mathop {\mathrm {r}}}(G),$ then 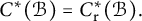$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$

Keywords

Fell bundlesinductionweak containmentabsorption principle

MSC classification

Primary: 46L99: None of the above, but in this section 22D25: $C^*$-algebras and $W^*$-algebras in relation to group representations
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abadie, F., Enveloping actions and Takai duality for partial actions . J. Funct. Anal. 197(2003), no. 1, 14–67.CrossRefGoogle Scholar
Abadie, F. and Ferraro, D., Equivalence of Fell bundles over groups . J. Operator Theory 81(2019), no. 2, 273–319.CrossRefGoogle Scholar
Anantharaman-Delaroche, C, Amenability and exactness for dynamical systems and their ${C}^{\ast}$ -algebras . Trans. Amer. Math. Soc. 354(2002), no. 10, 4153–4178.CrossRefGoogle Scholar
Blattner, R. J., On induced representations . Amer. J. Math. 83(1961), no. 1, 79–98.CrossRefGoogle Scholar
Buss, A., Echterhoff, S, and Willett, R, Amenability and weak containment for actions of locally compact groups on ${C}^{\ast}$ -algebras. Mem. Amer. Math. Soc. 301(2024), no. 1513, v+88 pp. ISBN: 978-1-4704-7152-1; 978-1-4704-7957-2Google Scholar
Derighetti, A., Some remarks on ${L}^1(G)$ . Math. Z. 164(1978), no. 2, 189–194.CrossRefGoogle Scholar
Exel, R., Partial dynamical systems, Fell bundles and applications, Mathematical Surveys and Monographs, 224, American Mathematical Society, Providence, RI, 2017.CrossRefGoogle Scholar
Exel, R and Ng, C.-K, Approximation property of ${C}^{\ast}$ -algebraic bundles . Math. Proc. Camb. Philos. Soc. 132(2002), 509–522.CrossRefGoogle Scholar
Fell, J. M. G., Induced representations and Banach ${}^{\ast}$ -algebraic bundles, Lecture Notes in Mathematics, 582, Springer-Verlag, Berlin and New York, 1977. With an appendix due to Douady, A. and Soglio-Hérault, L. Dal.Google Scholar
Fell, J. M. G and Doran, R. S., Representations of ${}^{\ast }$ -algebras, locally compact groups, and Banach ${}^{\ast}$ -algebraic bundles: Basic representation theory of groups and algebras. Vol. 1, Pure and Applied Mathematics, 125, Academic Press, Boston, MA, 1988a.Google Scholar
Fell, J. M. G and Doran, R. S, Representations of ${}^{\ast}$ -algebras, locally compact groups, and Banach ${}^{\ast }$ -algebraic bundles: Banach ${}^{\ast }$ -algebraic bundles, induced representations, and the generalized Mackey analysis. Vol. 2, Pure and Applied Mathematics, 126, Academic Press, Boston, MA, 1988b.Google Scholar
Kaliszewski, S, Landstad, M. B, and Quigg, J, Exotic group ${C}^{\ast}$ -algebras in noncommutative duality . New York J. Math. 19(2013), 689–711.Google Scholar
Mackey, G. W., Induced representations of locally compact groups. I . Ann. of Math. 2(1952), no. 55, 101–139.CrossRefGoogle Scholar
McKee, A. and Pourshahami, R., Amenable and inner amenable actions and approximation properties for crossed products by locally compact groups . Can. Math. Bull. 65(2020) no. 2, 381–399.CrossRefGoogle Scholar
Raeburn, I., On crossaed products by coactions and their representation theory . Proc. London Math. Soc. (3) 64(1992), no. (3), 25–652.Google Scholar
Raeburn, I. and Williams, D. P, Morita equivalence and continuous-trace ${C}^{\ast}$ -algebras. Vol. 60, American Mathematical Society, Providence, RI, 1998.CrossRefGoogle Scholar
Rieffel, M. A, Induced representations of ${C}^{\ast}$ -algebras . Adv. Math. 13(1974), 176–257.CrossRefGoogle Scholar