1.1 General notation

We will write $\mathbb {N}:=\left \{ 0,1,2,...\right \} $ and $\mathbb {N}_{\geq 1}:=\left \{ 1,2,...\right \} $ for the natural numbers. The neutral element of a group is always denoted by e, and for a set S, we write $\#S$ for the number of elements in S. Scalar products of Hilbert spaces are linear in the first variable, and we denote the bounded operators on a Hilbert space $\mathcal {H}$ by $\mathcal {B}(\mathcal {H})$ . Further, all Hilbert spaces and C $^{\ast }$ -algebras in this article are assumed to be separable. We write $\otimes $ for the spatial tensor product of C $^{\ast }$ -algebras as well as for tensor products of Hilbert spaces. For a discrete group G, we denote by $\ell ^{2}(G)$ the Hilbert space of all square summable functions $G\rightarrow \mathbb {C}$ and by $(\delta _{g})_{g\in G}$ the canonical orthonormal basis of $\ell ^2(G)$ .

1.2 Spectral triples and compact quantum metric spaces

One of the key concepts in the theory of noncommutative geometry is that of spectral triples introduced by Connes in [Reference Connes10].

Following Connes [Reference Connes10], given a spectral triple $(\mathcal {A},\mathcal {H},D)$ , one can define a Lipschitz semi-norm $L_{D}$ on $\mathcal {A}$ via

$$\begin{align*}L_{D}(a):=\left\Vert [D,\pi(a)]\right\Vert , \end{align*}$$

meaning that $L_{D}:\mathcal {A}\rightarrow \mathbb {R}_{+}$ is a semi-norm whose domain is a dense subspace of A that contains $1$ and for which $L_{D}(1)=0$ . (Note that there are various versions of this concept; here, we follow the conventions in [Reference Hawkins, Skalski, White and Zacharias18].) By [Reference Rieffel28, Proposition 3.7], the semi-norm $L_{D}$ is lower semi-continuous; that is, for every $r>0$ , the set $\{a\in \mathcal {A}\mid L_{D}(a)\leq r\}$ is closed in $\mathcal {A}$ with respect to the subspace topology. $L_{D}$ further induces a pseudo-metric $d_{L_{D}}:\mathcal {S}(A)\rightarrow [0,\infty ]$ on the state space $\mathcal {S}(A)$ of A via

$$\begin{align*}d_{L_{D}}(\psi,\psi^{\prime}):=\sup_{a\in \mathcal{A}:L_D(a)\leq1}|\psi(a)-\psi^{\prime}(a)|. \end{align*}$$

Note that $d_{L_D}$ may take value $+ \infty $ .

It is a natural question to ask when the topology on $\mathcal {S}(A)$ coming from $d_{L_{D}}$ coincides with the weak- $\ast $ topology (see [Reference Rieffel27], [Reference Rieffel28]). This is the defining property of a compact quantum metric space. One necessary condition for this to happen is that the triple $(\mathcal {A},\mathcal {H},D)$ is nondegenerate in the sense that the representation of $\mathcal {A}$ on $\mathcal {H}$ is faithful and $[D,\pi (a)]=0$ if and only if $a\in \mathbb {C}1$ . If the representation is faithful, we usually suppress it in the notation and view $\mathcal {A}$ and A as $\ast $ -subalgebras of $\mathcal {B}(\mathcal {H})$ .

Rieffel proved the following characterizations.

1.3 Horofunction compactifications

In [Reference Rieffel29], Rieffel demonstrated that (twisted) group C $^{\ast }$ -algebras of Abelian free groups $\mathbb {Z}^{m}$ , $m \in \mathbb {N}$ equipped with the natural Dirac operators coming from word length functions and restrictions of norms on Euclidean spaces, induce compact quantum metric spaces. His proof relies on the study of Gromov’s horofunction compactification (or metric compactification) of these groups and fixed points under the corresponding group action. Unfortunately, the approach does not cover other natural examples such as reduced group C $^{\ast }$ -algebras of word hyperbolic groups. Only later, this class of C $^{\ast }$ -algebras (and more generally a class of certain filtered C $^{\ast }$ -algebras) was treated by Ozawa and Rieffel in [Reference Ozawa and Rieffel24] by employing their notion of Haagerup-type condition. The results in [Reference Rieffel29] were extended to general nilpotent-by-finite groups by Christ and Rieffel in [Reference Christ and Rieffel8].

Going back to Gromov [Reference Gromov17] (see also [Reference Rieffel29]), the horofunction compactification of a metric space $(Y,d)$ is defined as follows. Consider the space $C(Y)$ of continuous functions on Y equipped with the topology of uniform convergence on bounded sets. For $y_{0}\in Y$ , define $C(Y,y_{0}):=\{f\in C(Y)\mid f(y_{0})=0\}$ . Then $C(Y,y_{0})$ is homeomorphic to $C_{\ast }(Y):=C(Y)/\mathbb {C}1$ equipped with the quotient topology, so in particular, $C(Y,y_{0})$ is independent of $y_{0}\in Y$ . One can define a continuous embedding of the space Y into $C(Y,y_{0})$ via $y\mapsto f_{y}(\, \cdot \,):=d(y, \, \cdot \,)-d(y,y_{0})$ . The corresponding closure of Y in $C(Y,y_{0})$ is denoted by $\widehat {Y}$ . If $(Y,d)$ is proper in the sense that every closed ball in Y is compact, $\widehat {Y}$ is a compact Hausdorff space which is called the horofunction compactification of Y. The action of the isometry group of Y extends to a continuous action on $\widehat {Y}$ by homeomorphism. The space $\partial Y:=\widehat {Y}\setminus Y$ equipped with the subspace topology is called the horofunction boundary of Y.

In [Reference Rieffel29, Section 4], it was shown that if $(Y,d)$ is a complete locally compact metric space, $C(\widehat {Y})$ can be described as the (commutative) unital C $^{\ast }$ -subalgebra $\mathcal {G}(Y,d)$ of $C_{b}(Y)$ generated by $C_{0}(Y)$ and the functions $Y\rightarrow \mathbb {C},y\mapsto f_{y}(x)$ where $x\in Y$ (i.e., $\widehat {Y}$ is homeomorphic to the character spectrum of $\mathcal {G}(Y,d)$ ).

An important notion in Rieffel’s work is that of weakly geodesic rays.

It can be shown that every almost geodesic ray is weakly geodesic. Further, the following theorem holds.

Theorem 1.5 [Reference Rieffel29, Theorem 4.7]

Let $(Y,d)$ be a complete locally compact metric space and let $\gamma :T\rightarrow Y\subseteq \widehat {Y}$ be a weakly geodesic ray. Then for every $f\in \mathcal {G}(Y,d)$ , the limit $\lim _{t\rightarrow \infty }f(\gamma (t))$ exists and gives a (unique) element in $\partial Y$ in the sense that

$$\begin{align*}\chi_{\gamma}:\mathcal{G}(Y,d)\rightarrow\mathbb{C},\chi_{\gamma}(f):=\lim_{t\rightarrow\infty}f(\gamma(t)) \end{align*}$$

defines a character on $\mathcal {G}(Y,d)$ whose restriction to $C_{0}(Y)$ vanishes. If Y is proper and if the topology of $(Y,d)$ has a countable base, then every point in $\partial Y$ is determined as above by a weakly geodesic ray.

In this article, we will mostly be concerned with the following setup that occurs in [Reference Connes10]. Let G be a discrete group equipped with a length function $\ell :G\rightarrow \mathbb {R}_{+}$ ; that is, $\ell (gh)\leq \ell (g)+\ell (h)$ and $\ell (g^{-1})=\ell (g)$ for all $g,h\in G$ , and $\ell (g)=0$ exactly if $g=e$ . Note that every such length function induces a natural metric $d_{\ell }$ on G via $d_{\ell }(g,h):=\ell (g^{-1}h)$ . The space $(G,d_{\ell })$ is proper if $\ell $ is proper in the sense that the set $\{g\in G\mid \ell (g)\leq r\}$ is finite for all $r>0$ . We will write $\overline {G}^{\ell }$ for the horofunction compactification of $(G,d_{\ell })$ and $\partial _{\ell }G$ for the corresponding boundary. The canonical action of G on itself via left multiplication extends to a continuous action $G\curvearrowright \overline {G}^{\ell }$ which again restricts to an action $G\curvearrowright \partial _{\ell }G$ on the boundary.

Prototypes of length functions on finitely generated groups are word length functions: for every discrete group G finitely generated by a set S with $S=S^{-1}$ , the expression $\ell _{S}(g):=\min \{n\mid g=s_{1}...s_{n}\text { where }s_{1},...,s_{n}\in S\}$ , $g\in G$ defines a length function on G.

2.1 Crossed product C $^{\ast }$ -algebras

Let $\alpha :G\rightarrow \text {Aut}(A)$ be an action of a discrete group G on a separable unital C $^{\ast }$ -algebra A and let $\ell :G\rightarrow \mathbb {R}_{+}$ be a proper length function on G. We will often write $g.a:=\alpha _{g}(a)$ , where $g\in G$ , $a\in A$ . Assume that $(\mathcal {A},\mathcal {H}_{A},D_{A})$ is an odd spectral triple on A via a faithful representation $\pi $ of A and consider the canonical odd spectral triple $(\mathbb {C}[G],\ell ^{2}(G),M_{\ell })$ on $C_{r}^{\ast }(G)$ . Here, $M_{\ell }$ denotes the multiplication operator given by $M_{\ell }\delta _{g}:=\ell (g)\delta _{g}$ for $g\in G$ , and $\mathbb {C}[G]\subseteq C_{r}^{\ast }(G)$ is the span of all left regular representation operators.

Recall that the reduced crossed product C $^{\ast }$ -algebra $A\rtimes _{\alpha ,r}G$ is defined as the C $^{\ast }$ -subalgebra of $\mathcal {B}(\mathcal {H}_{A}\otimes \ell ^{2}(G))$ generated by the operators $\widetilde {\pi }(a)$ , $a\in A$ and $\lambda _{g}$ , $g\in G$ with

$$\begin{align*}\widetilde{\pi}(a)(\xi\otimes\delta_{h}):=\pi(h^{-1}.a)\xi\otimes\delta_{h}\qquad\text{and}\qquad\lambda_{g}(\xi\otimes\delta_{h}):=\xi\otimes\delta_{gh} \end{align*}$$

for $\xi \in \mathcal {H}_{A}$ , $h\in G$ . This definition does (up to isomorphism) not depend on the choice of the faithful representation $\pi $ . The C $^{\ast }$ -algebra A naturally embeds into $A\rtimes _{\alpha ,r}G$ via $a\mapsto \widetilde {\pi }(a)$ . We will therefore often view A as a C $^{\ast }$ -subalgebra of $A\rtimes _{\alpha ,r}G$ and suppress $\pi $ and $\widetilde {\pi }$ in the notation. Further, we can canonically view the reduced group C $^\ast $ -algebra $C_{r}^{\ast }(G)$ as a C $^{\ast }$ -subalgebra of $A\rtimes _{\alpha ,r}G$ .

Proof The argument is standard; compare, for instance, with the proof of [Reference Brown and Ozawa3, Proposition 4.1.5]. Let $\pi :A\hookrightarrow \mathcal {B}(\mathcal {H}_{A})$ and $\pi ^{\prime }:A\hookrightarrow \mathcal {B}(\mathcal {H}_{A}^{\prime })$ be two faithful representations of A, define $\widetilde {\pi }$ and $\widetilde {\pi }^{\prime }$ as above, and consider

$$ \begin{align*} B_{1} & := C^{\ast}(\widetilde{\pi}(A)\cup\{\lambda_{g}\mid g\in G\}\cup\mathbb{C}1\otimes\ell^{\infty}(G))\subseteq\mathcal{B}(\mathcal{H}_{A}\otimes\ell^{2}(G)),\\ B_{2} & := C^{\ast}(\widetilde{\pi}^{\prime}(A)\cup\{\lambda_{g}\mid g\in G\}\cup\mathbb{C}1\otimes\ell^{\infty}(G))\subseteq\mathcal{B}(\mathcal{H}_{A}^{\prime}\otimes\ell^{2}(G)). \end{align*} $$

We have to show that $B_{1}\cong B_{2}$ via $\widetilde {\pi }(a)\mapsto \widetilde {\pi }^{\prime }(a)$ , $\lambda _{g}\mapsto \lambda _{g}$ and $1\otimes f\mapsto 1\otimes f$ for $a\in A$ , $g\in G$ , $f\in \ell ^{\infty }(G)$ . For every finite subset $F\subseteq G$ , define $P_{F}\in \ell ^{\infty }(G)$ to be the orthogonal projection onto the closure of $\text {Span}\{\delta _{g}\mid g\in F\}\subseteq \ell ^{2}(G)$ . It is then easy to see that for all finite sequences $(a_{g})_{g\in G}\subseteq A$ , $(f_{g})_{g\in G}\subseteq \ell ^{\infty }(G)$ with $a_{g}=0$ and $f_{g}=0$ for almost all $g\in G$ ,

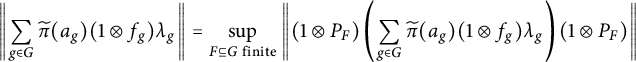$$\begin{align*}\left\Vert\sum_{g\in G}\widetilde{\pi}(a_{g})(1\otimes f_{g})\lambda_{g}\right\Vert=\sup_{F\subseteq G\text{ finite}}\left\Vert(1\otimes P_{F})\left(\sum_{g\in G}\widetilde{\pi}(a_{g})(1\otimes f_{g})\lambda_{g}\right)(1\otimes P_{F})\right\Vert \end{align*}$$

and

$$\begin{align*}\left\Vert\sum_{g\in G}\widetilde{\pi}^{\prime}(a_{g})(1\otimes f_{g})\lambda_{g}\right\Vert=\sup_{F\subseteq G\text{ finite}}\left\Vert(1\otimes P_{F})\left(\sum_{g\in G}\widetilde{\pi}^{\prime}(a_{g})(1\otimes f_{g})\lambda_{g}\right)(1\otimes P_{F})\right\Vert. \end{align*}$$

Now, for every finite subset $F\subseteq G$ and $a\in A$ ,

$$\begin{align*}(1\otimes P_{F})\widetilde{\pi}(a)=(1\otimes P_{F})\widetilde{\pi}(a)(1\otimes P_{F})=\sum_{h\in F}\widetilde{\pi}(h^{-1}.a)\otimes e_{h,h}, \end{align*}$$

where $e_{g,h}$ , $g,h\in F$ denote the canonical matrix units of $P_{F}\mathcal {B}(\ell ^{2}(G))P_{F}\cong M_{\#F}(\mathbb {C})$ . This implies that

$$ \begin{align*} (1\otimes P_{F})\left(\sum_{g\in G}\widetilde{\pi}(a_{g})(1\otimes f_{g})\lambda_{g}\right)(1\otimes P_{F}) & = \sum_{g\in G}\sum_{h\in F\cap gF}\widetilde{\pi}(h^{-1}.a_{g})\otimes(f_{g}e_{h,g^{-1}h})\\ & \in \widetilde{\pi}(A)\otimes M_{\#F}(\mathbb{C}), \end{align*} $$

and similarly for $\widetilde {\pi }^{\prime }$ . But $\widetilde {\pi }(A)\otimes M_{\#F}(\mathbb {C})\cong \widetilde {\pi }^{\prime }(A)\otimes M_{\#F}(\mathbb {C})$ canonically, and hence, the norms above coincide.

As in [Reference Hawkins, Skalski, White and Zacharias18, Section 2], define a Dirac operator D on $\mathcal {H}\oplus \mathcal {H}$ with $\mathcal {H}:=\mathcal {H}_{A}\otimes \ell ^{2}(G)$ via

$$\begin{align*}D:=\left(\begin{array}{cc} 0 & D_{A}\otimes1-i\otimes M_{\ell}\\ D_{A}\otimes1+i\otimes M_{\ell} & 0 \end{array}\right) \end{align*}$$

and write

$$\begin{align*}C_{c}(G,\mathcal{A}):=\left\{ \sum_{g\in G}a_{g}\lambda_{g}\mid(a_{g})_{g\in G}\subseteq\mathcal{A}\text{ with }a_{g}=0\text{ for almost all }g\in G\right\}. \end{align*}$$

Then $C_{c}(G,\mathcal {A})$ is a dense $\ast $ -subalgebra of $A\rtimes _{\alpha ,r}G\subseteq \mathcal {B}(\mathcal {H})$ . For $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,\mathcal {A})$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ , we call $\text {supp}(x):=\{g\in G\mid a_{g}\neq 0\}$ the support of x. It was argued in [Reference Hawkins, Skalski, White and Zacharias18, Theorem 2.7] that, under the assumption that $\mathcal {A}$ is invariant under the action of G and that $\sup _{g\in G}\left \Vert [D_{A},g.a]\right \Vert <\infty $ for every $a\in \mathcal {A}$ , the triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ defines an even spectral triple on $A\rtimes _{\alpha ,r}G$ . Further, if $(\mathcal {A},\mathcal {H}_{A},D_{A})$ is nondegenerate, so is $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ . (Note that in [Reference Hawkins, Skalski, White and Zacharias18], the slightly different setup of proper translation bounded integer-valued functions on G is considered; however, the results translate into our setting verbatim.) Motivated by this, let us introduce the notion of metrically equicontinuous actions.

Recall that the horofunction compactification $\overline {G}^{\ell }$ of a discrete group G equipped with a proper length function $\ell :G\rightarrow \mathbb {R}_{+}$ is the (compact) closure of the image of G in $C(G,e)$ under the embedding $g\mapsto f_{g}(\,\cdot \,):=d_{\ell }(g,\,\cdot \,)-d_{\ell }(g,e)$ and that the canonical action of G on itself induces actions $\beta :G\curvearrowright C(\overline {G}^{\ell })$ and $G\curvearrowright C(\partial _{\ell }G)$ . By the very construction, for every $g\in G$ , there exists a unique continuous bounded map $\varphi _{g}^{\ell }:\overline {G}^{\ell }\rightarrow \mathbb {C}$ defined by $\varphi _{g}^{\ell }(h):=\ell (h)-\ell (g^{-1}h)$ for $h\in G$ . These maps very naturally occur in our crossed product setting, as the following lemma illustrates.

Lemma 2.3 Let $\alpha :G\rightarrow \text {Aut}(A)$ be an action of a discrete group G on a separable unital C $^{\ast }$ -algebra $A\subseteq \mathcal {B}(\mathcal {H}_{A})$ and let $\ell :G\rightarrow \mathbb {R}_{+}$ be a proper length function on G. For every $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,A)\subseteq \mathcal {B}(\mathcal {H})$ with $(a_{g})_{g\in G}\subseteq A$ , $\mathcal {H}:=\mathcal {H}_{A}\otimes \ell ^{2}(G)$ ,

$$\begin{align*}[1\otimes M_{\ell},x]=\sum_{g\in G}(1\otimes\varphi_{g}^{\ell})a_{g}\lambda_{g}, \end{align*}$$

where $\varphi _{g}^{\ell }$ is viewed as a multiplication operator $\delta _{h}\mapsto \varphi _{g}^{\ell }(h)$ in $\ell ^{\infty }(G)\subseteq \mathcal {B}(\ell ^{2}(G))$ .

Proof One has that for every finite sum $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,\mathcal {A})$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ and $\xi \in \mathcal {H}$ , $h\in G$ ,

$$ \begin{align*} & [1\otimes M_{\ell},x](\xi\otimes\delta_{h})=(1\otimes M_{\ell})x(\xi\otimes\delta_{h})-x(1\otimes M_{\ell})(\xi\otimes\delta_{h})\\ & = \sum_{g\in G}\left(\ell(gh)-\ell(h)\right)(\alpha_{(gh)^{-1}}(a_{g})\xi\otimes\delta_{gh})=\sum_{g\in G}\varphi_{g}^{\ell}(gh)(\alpha_{(gh)^{-1}}(a_{g})\xi\otimes\delta_{gh}), \end{align*} $$

and hence,

$$\begin{align*}[1\otimes M_{\ell},x]=\sum_{g\in G}(1\otimes\varphi_{g}^{\ell})a_{g}\lambda_{g}\in\mathcal{B}(\mathcal{H}), \end{align*}$$

which implies the claim.

The maps $\varphi _{g}^{\ell }$ , $g\in G$ further satisfy the following 1-cocycle condition which will become important in the later sections.

Proof For all $g,h,x\in G$ ,

$$ \begin{align*} \varphi_{gh}^{\ell}(x) & = \ell(x)-\ell(h^{-1}g^{-1}x)\\ & = \ell(x)-\ell(g^{-1}x)+\ell(g^{-1}x)-\ell(h^{-1}g^{-1}x)\\ & = \varphi_{g}^{\ell}(x)+\varphi_{h}^{\ell}(g^{-1}x). \end{align*} $$

The claim then follows from the fact that the functions $\varphi _{gh}^{\ell }$ , $\varphi _{g}^{\ell }$ , and $\varphi _{h}^{\ell }$ are continuous and that G is dense in $\overline {G}^{\ell }$ .

By the discussion in Subsection 1.3, the commutative C $^{\ast }$ -algebra $C(\overline {G}^{\ell })$ is isomorphic to the unital C $^{\ast }$ -subalgebra $\mathcal {G}(G,\ell )$ of $\ell ^{\infty }(G)$ generated by $C_{0}(G)$ and the set $\{\varphi _{g}^{\ell }\mid g\in G\}$ , where again the $\varphi _{g}^{\ell }$ are viewed as multiplication operators. In the setting from before, define $\mathcal {C}(A,G,\ell )$ as the C $^{\ast }$ -subalgebra of $\mathcal {B}(\mathcal {H})$ generated by A, $\mathbb {C}1\otimes \mathcal {G}(G,\ell )$ and $C_{r}^{\ast }(G)$ . Then, $[1\otimes M_{l},x]\in \mathcal {C}(A,G,\ell )$ for every $x\in C_{c}(G,\mathcal {A})$ .

For the sake of transparency, let us in the following denote the canonical embeddings of A and $\mathcal {G}(G,\ell )\cong C(\overline {G}^{\ell })$ by

$$ \begin{align*} \nonumber \widetilde{\pi} &: A\hookrightarrow\mathcal{C}(A,G,\ell)\subseteq\mathcal{B}(\mathcal{H}),\\ \nonumber \pi_{\rtimes} &: A\hookrightarrow A\rtimes_{\alpha,r}G\subseteq\mathcal{B}(\mathcal{H}),\\ \nonumber \nu &: \mathcal{G}(G,\ell)\hookrightarrow\mathcal{B}(\ell^{2}(G)),\\ \nonumber \widetilde{\nu} &: \mathcal{G}(G,\ell)\hookrightarrow\mathcal{C}(A,G,\ell)\subseteq\mathcal{B}(\mathcal{H}), \\ \nonumber \nu_{\rtimes} &: \mathcal{G}(G,\ell)\hookrightarrow C(\overline{G}^{\ell})\rtimes_{\beta,r}G. \end{align*} $$

Similarly, denote the left regular representation operators in $\mathcal {C}(A,G,\ell )\subseteq \mathcal {B}(\mathcal {H})$ by $\widetilde {\lambda }_{g}$ , $g\in G$ and the ones in $\mathcal {B}(\ell ^{2}(G))$ , $A\rtimes _{\alpha ,r}G\subseteq \mathcal {B}(\mathcal {H})$ and $C(\overline {G}^{\ell })\rtimes _{\beta ,r}G$ by $\lambda _{g}$ , $g\in G$ . Note that $\widetilde {\pi }(a)=\pi _{\rtimes }(a)$ and $\widetilde {\lambda }_{g}=\lambda _{g}$ in $\mathcal {B}(\mathcal {H})$ for all $a\in A$ , $g\in G$ .

Proof One can view A as being covariantly and faithfully represented on $\mathcal {H}=\mathcal {H}_{A}\otimes \ell ^{2}(G)$ (via $\widetilde {\pi }$ from before). In turn, by applying Lemma 2.1, we can both interpret $\mathcal {C}(A,G,\ell )$ as a C $^{\ast }$ -subalgebra of $\mathcal {B}(\mathcal {H}\otimes \ell ^{2}(G))$ and as a C $^{\ast }$ -subalgebra of $\mathcal {B}(\mathcal {H})$ . Write $\iota $ for the corresponding embedding $\mathcal {C}(A,G,\ell )\hookrightarrow \mathcal {B}(\mathcal {H}\otimes \ell ^{2}(G))$ and define a unitary $U:\mathcal {H}\otimes \ell ^{2}(G)\rightarrow \mathcal {H}\otimes \ell ^{2}(G)$ via $U(\xi \otimes \delta _{g}):=\widetilde {\lambda }_{g}\xi \otimes \delta _{g}$ . For $a\in A$ , $\xi \in \mathcal {H}$ , $g\in G$ , one has

$$ \begin{align*} U(\iota\circ\widetilde{\pi})(a)U^{\ast}(\xi\otimes\delta_{g}) & = U(\iota\circ\widetilde{\pi})(a)(\widetilde{\lambda}_{g^{-1}}\xi\otimes\delta_{g})\\ & = U(\alpha_{g^{-1}}(\widetilde{\pi}(a))\widetilde{\lambda}_{g^{-1}}\xi\otimes\delta_{g})\\ & = U(\widetilde{\lambda}_{g^{-1}}\widetilde{\pi}(a)\xi\otimes\delta_{g})\\ & = \widetilde{\pi}(a)\xi\otimes\delta_{g} \\ \nonumber &= \pi_{\rtimes}(a)\xi\otimes\delta_{g}, \end{align*} $$

so $U(\iota \circ \widetilde {\pi })(a)U^{\ast }=\pi _{\rtimes }(a)\otimes 1$ . For $f\in C(\overline {G}^{\ell })\cong \mathcal {G}(G,\ell )$ , $\xi \in \mathcal {H}$ , $g\in G$ ,

$$ \begin{align*} U(\iota\circ\widetilde{\nu}(f))U^{\ast}(\xi\otimes\delta_{g}) & = U(\iota\circ\widetilde{\nu})(f)(\widetilde{\lambda}_{g^{-1}}\xi\otimes\delta_{g})\\ & = f(g)U(\widetilde{\lambda}_{g^{-1}}\xi\otimes\delta_{g})\\ & = f(g)(\xi\otimes\delta_{g}), \end{align*} $$

so $U(\iota \circ \widetilde {\nu })(f)U^{\ast }=1\otimes \nu (f)$ . Lastly, for $\xi \in \mathcal {H}$ , $g,h\in G$ ,

$$ \begin{align*} U\iota(\widetilde{\lambda}_{g})U^{\ast}(\xi\otimes\delta_{h}) & = U\iota(\widetilde{\lambda}_{g})(\widetilde{\lambda}_{h^{-1}}\xi\otimes\delta_{h})\\ & = U(\widetilde{\lambda}_{h^{-1}}\xi\otimes\delta_{gh})\\ & = \widetilde{\lambda}_{g}\xi\otimes\delta_{gh} \\ \nonumber &= \lambda_{g}\xi\otimes\delta_{gh}, \end{align*} $$

so $U\iota (\widetilde {\lambda }_{g})U^{\ast }=\lambda _{g}\otimes \lambda _{g}$ . This implies that conjugation by U implements a $\ast $ -embedding of $\mathcal {C}(A,G,\ell )$ into $(A\rtimes _{\alpha ,r}G)\otimes C_{u}^{\ast }(G)$ via $\widetilde {\pi }(a)\mapsto \pi _{\rtimes }(a)\otimes 1$ , $\widetilde {\nu }(f)\mapsto 1\otimes \nu (f)$ and $\widetilde {\lambda }_{g}\mapsto \lambda _{g}\otimes \lambda _{g}$ for $a\in A$ , $f\in C(\overline {G}^{\ell })\cong \mathcal {G}(G,\ell )$ and $g\in G$ . Here, $C_{u}^{\ast }(G)\subseteq \mathcal {B}(\ell ^{2}(G))$ denotes the uniform Roe algebra which is generated by $\ell ^{\infty }(G)$ and $C_{r}^{\ast }(G)$ in $\mathcal {B}(\ell ^{2}(G))$ . By [Reference Brown and Ozawa3, Proposition 5.1.3], $C_{u}^{\ast }(G)\cong \ell ^{\infty }(G)\rtimes _{r}G$ canonically where the crossed product is taken with respect to the left translation action. In particular, the C $^{\ast }$ -subalgebra of $\mathcal {B}(\ell ^{2}(G))$ generated by $\mathcal {G}(G,\ell )$ and $C_{r}^{\ast }(G)$ identifies with $C(\overline {G}^{\ell })\rtimes _{\beta ,r}G$ . We deduce the claim.

Note that the proof of Proposition 2.5 does not require the action $\beta $ to be amenable.

For notational convenience, if S is a subset of G, we define

$$\begin{align*}C_{c}(S,\mathcal{A}):=\left\{ \sum_{g\in S}a_{g}\lambda_{g}\mid(a_{g})_{g\in G}\subseteq\mathcal{A}\text{ with }a_{g}=0\text{ for almost all }g\in S\right\} \subseteq A\rtimes_{\alpha,r}G \end{align*}$$

and $C_{c}(S,A)\subseteq A\rtimes _{\alpha ,r}G$ analogously. If S is a subgroup of G, then these spaces will be $\ast $ -subalgebras of $A\rtimes _{\alpha ,r}G$ .

Proof Let $(g_{i})_{i\in I}\subseteq G$ be a family of elements with $G=\bigcup _{i\in I}Hg_{i}$ and $Hg_{i}\neq Hg_{j}$ for $i\neq j$ . For $i\in I$ , write $P_{Hg_{i}}$ for the orthogonal projection onto the closed subspace of $\ell ^{2}(G)$ spanned by all orthonormal basis vectors $\delta _{hg_{i}}$ , $h\in H$ . We claim that the linear map $\mathbb {E}_{H}$ given by $x\mapsto \sum _{i\in I}(1\otimes P_{Hg_{i}})x(1\otimes P_{Hg_{i}})$ satisfies the required conditions, where the sum converges in the strong operator topology. Indeed, for every $x\in \mathcal {B}(\mathcal {H})$ ,

$$\begin{align*}\left\Vert\sum_{i\in I}(1\otimes P_{Hg_{i}})x(1\otimes P_{Hg_{i}})\right\Vert\leq\sup_{i\in I}\left\Vert (1\otimes P_{Hg_{i}})x(1\otimes P_{Hg_{i}})\right\Vert \leq\left\Vert x\right\Vert , \end{align*}$$

as the operators $(1\otimes P_{Hg_{i}})x(1\otimes P_{Hg_{i}})$ , $i\in I$ have pairwise orthogonal support and ranges. For $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,\mathcal {A})\subseteq \mathcal {B}(\mathcal {H})$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ and $\xi \in \mathcal {H}_{A}$ , $h^{\prime }\in H$ , $i\in I$ , we further find

$$ \begin{align*} \nonumber \left(\mathbb{E}_{H}(x)\right)(\xi\otimes\delta_{h^{\prime}g_{i}}) &= ((1\otimes P_{Hg_{i}})\sum_{g\in G}a_{g}\lambda_{g})(\xi\otimes\delta_{h^{\prime}g_{i}}) \\ \nonumber &= \sum_{g\in G}(1\otimes P_{Hg_{i}})\left(((gh^{\prime}g_{i})^{-1}.a_{g})\xi\otimes\delta_{gh^{\prime}g_{i}}\right) \\ \nonumber &= \sum_{h\in H}\left(((hh^{\prime}g_{i})^{-1}.a_{h})\xi\otimes\delta_{hh^{\prime}g_{i}}\right) \\ \nonumber &= \left(\sum_{h\in H}a_{h}\lambda_{h}\right)(\xi\otimes\delta_{h^{\prime}g_{i}}), \end{align*} $$

so that $\mathbb {E}_{H}(x)=\sum _{h\in H}a_{h}\lambda _{h}$ . For $g,g^{\prime }\in G$ , there exist $i\in I$ and $h^{\prime }\in H$ such that $gg^{\prime }=h^{\prime }g_{i}$ . It follows that

$$ \begin{align*} \nonumber \left(\mathbb{E}_{H}([D_{A}\otimes1,x]\lambda_{g^{-1}})\lambda_{g}\right)(\xi\otimes\delta_{g^{\prime}}) &= \left((1\otimes P_{Hg_{i}})\sum_{g^{\prime\prime}\in G}[D_{A}\otimes1,a_{g^{\prime\prime}}]\lambda_{g^{\prime\prime}g^{-1}}\right)(\xi\otimes\delta_{h^{\prime}g_{i}}) \\ \nonumber &= \left(\sum_{g^{\prime\prime}\in Hg}[D_{A}\otimes1,a_{g^{\prime\prime}}]\lambda_{g^{\prime\prime}g^{-1}}\right)(\xi\otimes\delta_{h^{\prime}g_{i}}) \\ \nonumber &= \left(\sum_{g^{\prime\prime}\in Hg}[D_{A}\otimes1,a_{g^{\prime\prime}}]\lambda_{g^{\prime\prime}}\right)(\xi\otimes\delta_{g^{\prime}}) \\ \nonumber &= \left([D_{A}\otimes1,\mathbb{E}_{H}(x\lambda_{g^{-1}})\lambda_{g}]\right)(\xi\otimes\delta_{g^{\prime}}), \end{align*} $$

and with Lemma 2.3,

$$ \begin{align*} \nonumber \left(\mathbb{E}_{H}([1\otimes M_{\ell},x]\lambda_{g^{-1}})\lambda_{g}\right)(\xi\otimes\delta_{g^{\prime}}) &= ((1\otimes P_{Hg_{i}})\sum_{g\in G}(1\otimes\varphi_{g^{\prime\prime}}^{\ell})a_{g^{\prime\prime}}\lambda_{g^{\prime\prime}g^{-1}})(\xi\otimes\delta_{h^{\prime}g_{i}}) \\ \nonumber &= \left(\sum_{g^{\prime\prime}\in Hg}(1\otimes\varphi_{g^{\prime\prime}}^{\ell})a_{g^{\prime\prime}}\lambda_{g^{\prime\prime}g^{-1}}\right)(\xi\otimes\delta_{h^{\prime}g_{i}}) \\\nonumber &= \left(\sum_{g^{\prime\prime}\in Hg}(1\otimes\varphi_{g^{\prime\prime}}^{\ell})a_{g^{\prime\prime}}\lambda_{g^{\prime\prime}}\right)(\xi\otimes\delta_{g^{\prime}}) \\ \nonumber &= ([1\otimes M_{\ell},\mathbb{E}_{H}(x\lambda_{g^{-1}})\lambda_{g}])(\xi\otimes\delta_{g^{\prime}}). \end{align*} $$

We deduce that $\mathbb {E}_{H}([D_{A}\otimes 1,x]\lambda _{g^{-1}})\lambda _{g}=[D_{A}\otimes 1,\mathbb {E}_{H}(x\lambda _{g^{-1}})\lambda _{g}]$ and $\mathbb {E}_{H}([1\otimes M_{\ell },x]\lambda _{g^{-1}})\lambda _{g}=[1\otimes M_{\ell },\mathbb {E}_{H}(x\lambda _{g^{-1}})\lambda _{g}]$ , as claimed.

2.2 Crossed product C $^{\ast }$ -algebras as compact quantum metric spaces

Consider the setting of Subsection 2.1; that is, let $(\mathcal {A},\mathcal {H}_{A},D_{A})$ be a nondegenerate odd spectral triple on a separable unital C $^{\ast }$ -algebra A and assume that the induced Lipschitz semi-norm $L_{D_{A}}(a):=\left \Vert [D_{A},a]\right \Vert ,a\in \mathcal {A}$ defines a compact quantum metric space $(A,L_{D_{A}})$ . Let further $\alpha :G\rightarrow \text {Aut}(A)$ be a metrically equicontinuous action of a discrete group and $\ell :G\rightarrow \mathbb {R}_{+}$ a proper length function on G. It is natural to ask whether the even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ defined in Subsection 2.1 induces a Lip-metric on the state space of $A\rtimes _{\alpha ,r}G$ . This question was formulated in [Reference Hawkins, Skalski, White and Zacharias18] in the case of $G=\mathbb {Z}$ and length functions induced by finite symmetric generating sets. The discussion in [Reference Hawkins, Skalski, White and Zacharias18, Subsection 2.3] implies the following convenient criterion. We include its proof for the convenience of the reader.

Proposition 2.7 [Reference Hawkins, Skalski, White and Zacharias18, Subsection 2.3]

The even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ defined in Subsection 2.1 is a spectral metric space if and only if the set

(2.1) $$ \begin{align} \left\{ x\in C_{c}(G,\mathcal{A})\mid\left\Vert [D_{A}\otimes1,x]\right\Vert \leq1\text{ and }\left\Vert [1\otimes M_{\ell},x]\right\Vert \leq1\right\} \end{align} $$

has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ .

Proof By Theorem 1.3, the even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space if and only if the set $\mathcal {Q}:=\{x\in C_{c}(G,\mathcal {A})\mid \Vert [D,x\oplus x]\Vert \leq 1\}$ has totally bounded image in the quotient space $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . Denote the set in (2.1) by $\mathcal {Q}^{\prime }$ .

“ $\Rightarrow $ ” Assume that the even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space. For $x=\sum _{g\in G}a_{g}\lambda _{g}\in \mathcal {Q}^{\prime }$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ , we have by

(2.2) $$ \begin{align} [D,x\oplus x]=\left(\begin{array}{cc} 0 & [D_{A}\otimes1,x]-i[1\otimes M_{\ell},x]\\{} [D_{A}\otimes1,x]+i[1\otimes M_{\ell},x] & 0 \end{array}\right) \end{align} $$

that

$$\begin{align*}\Vert[D,x\oplus x]\Vert\leq2\Vert[D_{A}\otimes1,x]\Vert+2\Vert[1\otimes M_{\ell},x]\Vert\leq4. \end{align*}$$

This means that $\mathcal {Q}^{\prime }\subseteq 4\mathcal {Q}$ , and therefore, the image of $\mathcal {Q}^{\prime }$ must be totally bounded in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ .

“ $\Leftarrow $ ” Assume that the image of $\mathcal {Q}^{\prime }$ is totally bounded in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . From (2.2), it follows that $\Vert [D_{A}\otimes 1,x]+i[1\otimes M_{\ell },x]\Vert \leq 1$ and $\Vert [D_{A}\otimes 1,x]-i[1\otimes M_{\ell },x]\Vert \leq 1$ for every $x\in \mathcal {Q}$ . But then, $\Vert [D_{A}\otimes 1,x]\Vert \leq 2$ and $\Vert [1\otimes M_{\ell },x]\Vert \leq 2$ , and therefore, $\mathcal {Q}\subseteq 2\mathcal {Q}^{\prime }$ . We conclude that the image of $\mathcal {Q}$ in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ must be totally bounded, and therefore, the triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space.

Proposition 2.7 implies that in the treatment of the question above, it suffices to restrict to cosets of finite index subgroups.

Proof Set $\mathcal {Q}:=\left \{ x\in C_{c}(G,\mathcal {A})\mid \left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1\text { and }\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1\right \}, $ and for $g\in G$ , write $\mathcal {Q}_{g}$ for the set of all elements $x=\sum _{h\in H}a_{h}\lambda _{hg}\in C_{c}(Hg,\mathcal {A})$ with $(a_{h})_{h\in H}\subseteq \mathcal {A}$ satisfying $\left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ and $\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1$ .

“ $\Rightarrow $ ” Assume that the triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space. By Proposition 2.7, the set $\mathcal {Q}$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . But $\mathcal {Q}_{g}$ is contained in $\mathcal {Q}$ . It follows that $\mathcal {Q}_{g}$ must also have totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ .

“ $\Leftarrow $ ” Assume that $\mathcal {Q}_{g}$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ for every $g\in G$ and let $g_{1},...,g_{m}\in G$ be elements with $G=\bigcup _{i=1}^{m}Hg_{i}$ and $Hg_{i}\neq Hg_{j}$ for $i\neq j$ . For $x=\sum _{g\in G}a_{g}\lambda _{g}\in \mathcal {Q}$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ and $i=1,...,m$ , set $x_{i}:=\sum _{h\in H}a_{hg_{i}}\lambda _{hg_{i}}$ . Then $x=x_{1}+...+x_{m}$ ,

$$ \begin{align*} \left\Vert [1\otimes M_{\ell},x_{i}]\right\Vert & = \left\Vert\sum_{h\in H}(1\otimes\varphi_{hg_{i}})a_{hg_{i}}\lambda_{hg_{i}}\right\Vert\\ &= \Vert[1\otimes M_{\ell},\mathbb{E}_{H}(x\lambda_{g_{i}^{-1}})\lambda_{g_{i}}]\Vert \\ & = \Vert\mathbb{E}_{H}([1\otimes M_{\ell},x]\lambda_{g_{i}^{-1}})\lambda_{g_{i}}\Vert\\ & \leq \left\Vert [1\otimes M_{\ell},x]\right\Vert \\ & \leq 1,\\[-18.5pt] \end{align*} $$

where $\mathbb {E}_{H}$ is the contractive linear map appearing in Lemma 2.6, and similarly,

$$\begin{align*}\left\Vert [D_{A}\otimes1,x_{i}]\right\Vert =\Vert\mathbb{E}_{H}([D_{A}\otimes1,x]\lambda_{g_{i}^{-1}})\lambda_{g_{i}}\Vert\leq\Vert[D_{A}\otimes1,x]\Vert\leq1. \end{align*}$$

It follows that $\mathcal {Q}\subseteq \mathcal {Q}_{g_{1}}+...+\mathcal {Q}_{g_{m}}$ , and hence, since the $\mathcal {Q}_{g_{i}}$ are assumed to have totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ , the set $\mathcal {Q}$ also has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . With Proposition 2.7, we deduce that the triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space.

For a group G, we denote its (normal) commutator subgroup (or derived subgroup) generated by all commutators $[g,h]:=g^{-1}h^{-1}gh$ , $g,h\in G$ by $[G,G]$ . Its Abelianization is the commutative group $G/[G,G]$ . If G is finitely generated, then so is its Abelianization, which can therefore be written as a direct product $T\times \mathbb {Z}^{m}$ , where $m\geq 0$ is the rank of $G/[G,G]$ and where T is its torsion subgroup.

Recall that an invariant mean of a discrete group G is a state on $\ell ^{\infty }(G)\subseteq \mathcal {B}(\ell ^{2}(G))$ that is invariant under the canonical action of G. A group G is amenable if it admits an invariant mean.

As it will be convenient in Section 3, we formulate the following lemma as well as Definition 2.10 for pseudo-length functions instead of just length functions. A pseudo-length function on a discrete group G is a map $\ell :G\rightarrow \mathbb {R}_{+}$ satisfying $\ell (gh)\leq \ell (g)+\ell (h)$ , $\ell (g^{-1})=\ell (g)$ for all $g,h\in G$ and $\ell (e)=0$ . As before, associate bounded operators $\varphi _{g}^{\ell }\in \ell ^{\infty }(G)\subseteq \mathcal {B}(\ell ^{2}(G))$ , $g\in G$ with $\ell $ by defining $\varphi _{g}^{\ell }\delta _{h}:=(\ell (h)-\ell (g^{-1}h))\delta _{h}$ for $h\in G$ . It is easy to check that the 1-cocycle identity in Lemma 2.4 holds for (not necessarily proper) pseudo-length functions as well.

The fundamental idea of our approach consists of showing that for suitable groups and (pseudo-)length functions on them, the space of all invariant means is sufficiently rich in the sense that it induces many nontrivial group homomorphisms as in Lemma 2.9. Let us therefore introduce the following notion.

Definition 2.10 Let G be a finitely generated discrete group equipped with a pseudo-length function $\ell $ and let $p_{G}$ be the projection onto the torsion-free component of the Abelianization of G. We call G separated with respect to $\ell $ if

$$\begin{align*}\text{Hom}(\text{im}(p_{G}),\mathbb{R})=\text{Span}\left\{ \widehat{\mu}_{\ell}\mid\mu\text{ invariant mean}\right\}. \end{align*}$$

In this case, we also say that the pair $(G,\ell )$ is separated.

It is clear that every group that is separated with respect to a certain length function has to be amenable.

For notational convenience, for subsets $S,T$ of a C $^{\ast }$ -algebra A and $\varepsilon>0$ , we write $S\subseteq _{\varepsilon }T$ if for every $a\in S$ , there exists $b\in T$ with $\left \Vert a-b\right \Vert <\varepsilon $ . For $\lambda>0$ , we further denote the set of all elements $\lambda a$ with $a\in S$ by $\lambda S$ .

Proposition 2.11 Let G be a finitely generated discrete group equipped with a proper length function $\ell :G\rightarrow \mathbb {R}_{+}$ . Assume that G admits a finite index subgroup H that is separated with respect to the restriction of $\ell $ to H and let $A\subseteq \mathcal {B}(\mathcal {H}_{A})$ be a unital separable C $^{\ast }$ -algebra on which G acts. For every $g\in G$ , define

$$\begin{align*}\mathcal{Q}_{1}^{g}:=\left\{ x\in C_{c}(Hg,A)\mid\left\Vert [1\otimes M_{\ell},x]\right\Vert \leq1\right\}. \end{align*}$$

Then for every $\varepsilon>0$ , there exists $\delta>0$ and finitely many elements $g_{1},...,g_{n}\in G$ such that $\mathcal {Q}_{1}^{g}\subseteq _{\varepsilon }\delta \mathcal {Q}_{1}^{g}\cap C_{c}(K,A)$ , where $K:=\bigcup _{i=1}^{n}[H,H]g_{i}$ .

Similarly, if $(\mathcal {A},\mathcal {H}_{A},D_{A})$ is a nondegenerate spectral triple on A, $g\in G$ and

$$\begin{align*}\mathcal{Q}_{2}^{g}:=\left\{ x\in C_{c}(Hg,\mathcal{A})\mid\left\Vert [1\otimes M_{\ell},x]\right\Vert \leq1,\left\Vert [D_{A}\otimes1,x]\right\Vert \leq1\right\} , \end{align*}$$

then for every $\varepsilon>0$ , there exists $\delta>0$ and finitely many elements $g_{1},...,g_{n}\in G$ such that $\mathcal {Q}_{2}^{g}\subseteq _{\varepsilon }\delta \mathcal {Q}_{2}^{g}\cap C_{c}(K,\mathcal {A})$ , where $K:=\bigcup _{i=1}^{n}[H,H]g_{i}$ .

Roughly speaking, Proposition 2.11 states that all elements $x\in C_{c}(Hg,A)$ , $g\in G$ with $\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1$ (and $\left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ ) can suitably be approximated by ones that are in some sense almost supported on the commutator subgroup of H. This has important implications. The proof of the proposition relies on the following variation of the result in [Reference Ozawa and Rieffel24, Section 2].

Lemma 2.12 Let G be a finitely generated discrete group equipped with a proper length function $\ell :G\rightarrow \mathbb {R}_{+}$ , let $\alpha :G\rightarrow \text {Aut}(A)$ an action of G on a unital separable C $^{\ast }$ -algebra $A\subseteq \mathcal {B}(\mathcal {H}_{A})$ , and let $L\in \mathbb {R}$ . For a nontrivial group homomorphism $\phi :G\rightarrow \mathbb {Z}$ , define an unbounded operator $M_{\phi }$ on $\ell ^{2}(G)$ via $M_{\phi }\delta _{g}:=\phi (g)\delta _{g}$ for $g\in G$ . Then for every $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,A)$ with $(a_{g})_{g\in G}\subseteq A$ , the operator $[1\otimes M_{\phi },x]$ has dense domain and is bounded. Further,

$$\begin{align*}\left\Vert\sum_{g\in G:\left|\phi(g)\right|>N}a_{g}\lambda_{g}\right\Vert\leq\left(\sum_{k\in\mathbb{Z}:\left|k\right|>N}\frac{1}{(k+L)^{2}}\right)^{1/2}\left\Vert [1\otimes M_{\phi},x] + Lx \right\Vert \end{align*}$$

for every $N\in \mathbb {N}$ with $N\geq \left |L\right |$ .

Proof It is clear that $[1\otimes M_{\phi },x]$ has dense domain, and by the same computation as in the proof of Lemma 2.3,

$$\begin{align*}[1\otimes M_{\phi},x]=\sum_{g\in G}\phi(g)a_{g}\lambda_{g}, \end{align*}$$

so $[1\otimes M_{\phi },x]$ is bounded. To prove the inequality, define a strong operator-continuous 1-parameter family $\mathbb {R}\rightarrow \mathcal {B}(\mathcal {H}_{A}\otimes \ell ^{2}(G))$ , $t\mapsto U_{t}$ via $U_{t}(\xi \otimes \delta _{g}):=e^{it\phi (g)}(\xi \otimes \delta _{g})$ for $\xi \in \mathcal {H}_{A}$ , $g\in G$ . For fixed $N\in \mathbb {N}$ with $N\geq \left |L\right |$ , we obtain a bounded linear map on $\mathcal {B}(\mathcal {H}_{A}\otimes \ell ^{2}(G))$ via $\kappa (x)\eta :=(2\pi )^{-1}\int _{0}^{2\pi }f_{N}(t)U_{t}xU_{t}^{\ast }\eta dt$ for $\eta \in \mathcal {H}_{A}\otimes \ell ^{2}(G)$ with the $L^{2}$ -function $f_{N}(t):=\sum _{k\in \mathbb {Z}:\left |k\right |>N}(k+L)^{-1}e^{-ikt}$ with prescribed Fourier coefficients $(k+L)^{-1}$ for $|k|>N$ . Then, for $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,A)$ with $(a_{g})_{g\in G}\subseteq A$ and $\xi \in \mathcal {H}_{A}$ , $h\in G$ ,

$$ \begin{align*} \left[\kappa([1\otimes M_{\phi},x]+Lx)\right](\xi\otimes\delta_{h}) & = \sum_{g\in G}\frac{\phi(g)+L}{2\pi}\left\{ \int_{0}^{2\pi}e^{it\phi(g)}f_{N}(t)dt\right\} \left(((gh)^{-1}.a_{g})\xi\otimes\delta_{gh}\right)\\ & = \sum_{g\in G:\left|\phi(g)\right|>N}\left(((gh)_{.}^{-1}a_{g})\xi\otimes\delta_{gh}\right). \end{align*} $$

We get that $\kappa ([1\otimes M_{\phi },x]+Lx)=\sum _{g\in G:\left |\phi (g)\right |>N}a_{g}\lambda _{g},$ and hence,

$$ \begin{align*} & \left\Vert\sum_{g\in G:\left|\phi(g)\right|>N}a_{g}\lambda_{g}\right\Vert=\left\Vert \kappa([1\otimes M_{\phi},x]+Lx)\right\Vert \leq\frac{\left\Vert [1\otimes M_{\phi},x]+Lx\right\Vert }{2\pi}\int_{0}^{2\pi}\left|f_{N}(t)\right|dt\\ & \leq \frac{\left\Vert [1\otimes M_{\phi},x]+Lx\right\Vert }{\sqrt{2\pi}}\left(\int_{0}^{2\pi}\left|f_{N}(t)\right|{}^{2}dt\right)^{1/2}=\left(\sum_{k\in\mathbb{Z}:\left|k\right|>N}\frac{1}{(k+L)^{2}}\right)^{1/2}\left\Vert [1\otimes M_{\phi},x] + Lx \right\Vert. \end{align*} $$

We are now ready to prove Proposition 2.11. As mentioned earlier, Rieffel’s approach in [Reference Rieffel29] relies on the construction of sufficiently many fixed points in the horofunction boundaries of $\mathbb {Z}^{m}$ , $m\in \mathbb {N}$ . These fixed points induce conditional expectations from the crossed product C $^{\ast }$ -algebra associated with the horofunction compactification onto the group C $^{\ast }$ -algebra $C_{r}^{\ast }(\mathbb {Z}^{m})$ . Similarly, in the proof of Proposition 2.11, we will make use of the assumption that $(G,\ell )$ is separated to construct suitable maps onto the restricted crossed product C $^{\ast }$ -algebra $A\rtimes _{\alpha |_{H},r}H$ .

Proof of Proposition 2.11

We only prove the second statement of Proposition 2.11 since the first one follows similarly. So assume that $(\mathcal {A},\mathcal {H}_{A},D_{A})$ is a nondegenerate odd spectral triple on A, $g\in G$ , pick $x=\sum _{h\in H}a_{h}\lambda _{hg}\in C_{c}(Hg,A)$ with $(a_{h})_{h\in H}\subseteq \mathcal {A}$ , $\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1$ , $\left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ , and fix $\varepsilon>0$ . As before, let $p_{H}:H\twoheadrightarrow \mathbb {Z}^{m}$ be the projection onto the torsion-free component of the Abelianization of H (i.e. m is the rank of the finitely generated Abelian group $H/[H,H]$ ). By our assumption, H is separated with respect to the restriction $\ell |_{H}$ . We can therefore find linear combinations $\phi _{1},...,\phi _{m}$ of invariant means on $\ell ^{\infty }(H)$ such that $\phi _{i}(\varphi _{h}^{\ell |_{H}})=p_{i}\circ p_{H}(h)$ for every $h\in H$ , $1\leq i\leq m$ , where $p_{i}:\mathbb {Z}^{m}\rightarrow \mathbb {Z}$ is the projection onto the i-th component of $\mathbb {Z}^{m}$ . These functionals induce maps $\ell ^{\infty }(G)\rtimes _{\beta |_{H},r}H\rightarrow C_{r}^{\ast }(H)$ via $f\lambda _{h}\mapsto \phi _{i}(f|_{H})\lambda _{h}$ for $f\in \ell ^{\infty }(G)$ , $h\in H$ and composition with the isomorphism from Proposition 2.5, and an application of Fell’s absorption principle (see [Reference Brown and Ozawa3, Proposition 4.1.7]) leads to bounded maps $P_{i}:\mathcal {C}(A,H,\ell )\rightarrow A\rtimes _{\alpha |_H,r}H$ via $P_{i}(a(1\otimes f)\lambda _{h}):=\phi _{i}(f|_{H})a\lambda _{h}$ for $a\in A$ , $f\in \mathcal {G}(G,\ell )$ , $h\in H$ . Here, $\mathcal {C}(A,H,\ell )$ is the C $^{\ast }$ -subalgebra of $\mathcal {B}(\mathcal {H})$ with $\mathcal {H}:=\mathcal {H}_{A}\otimes \ell ^{2}(G)$ generated by A, $\mathbb {C}1\otimes \mathcal {G}(G,\ell )$ and $C_{r}^{\ast }(H)$ . For every i, write $\mathbb {E}_{i}$ for the contractive linear map on $\mathcal {B}(\mathcal {H})$ associated with the subgroup $\text {ker}(p_i \circ p_H) \leq G$ as in Lemma 2.6.

We proceed inductively. Define $L:=\max \{\left \Vert P_{1}\right \Vert ,...,\left \Vert P_{m}\right \Vert \}$ and note that $\varphi _{h}^{\ell |_{H}}=\varphi _{h}^{\ell }|_{H}$ for every $h\in H$ . By applying $P_{1}$ to $[1\otimes M_{\ell },x]\lambda _{g^{-1}}\in \mathcal {C}(A,H,\ell )$ and by using the identity in Lemma 2.3, we find

$$ \begin{align*} \nonumber \Vert\phi_{1}(\varphi_{g}^{\ell}|_{H})x\lambda_{g^{-1}}+[1\otimes M_{p_{1}\circ p_{H}},x\lambda_{g^{-1}}]\Vert &= \left\Vert\sum_{h\in H}\left\{ \phi_{1}(\varphi_{g}^{\ell}|_{H})+p_{1}\circ p_{H}(h)\right\} a_{h}\lambda_{h}\right\Vert \\ \nonumber &= \left\Vert\sum_{h\in H}\phi_{1}(\varphi_{hg}^{\ell}|_{H})a_{h}\lambda_{h}\right\Vert \\ \nonumber &= \left\Vert P_{1}([1\otimes M_{\ell},x]\lambda_{g^{-1}})\lambda_{g}\right\Vert \\ \nonumber &\leq L. \end{align*} $$

In combination with Lemma 2.12 (where the constant is taken to be $\phi _{1}(\varphi _{g}^{\ell }|_{H})$ ), this implies that there exists $N_{1}\in \mathbb {N}$ (which is independent of $x\in \mathcal {Q}_{2}^{g}$ ) with

$$\begin{align*}\left\Vert\sum_{h\in H:\left|p_{1}\circ p_{H}(h)\right|>N_{1}}a_{h}\lambda_{hg}\right\Vert\leq\left\Vert\sum_{h\in H:\left|p_{1}\circ p_{H}(h)\right|>N_{1}}a_{h}\lambda_{h}\right\Vert\leq m^{-1}\varepsilon. \end{align*}$$

For every $-N_{1}\leq i\leq N_{1}$ , choose $h_{i}\in H$ with $p_{1}\circ p_{H}(h_{i})=i$ and define an element in the crossed product via $x_{1}:=\sum _{h\in H:\left |p_{1}\circ p_{H}(h)\right |\leq N_{1}}a_{h}\lambda _{hg}\in A\rtimes _{\alpha ,r}G$ . Then $\left \Vert x-x_{1}\right \Vert \leq m^{-1}\varepsilon $ ,

$$ \begin{align*} \Vert[1\otimes M_{\ell},x_{1}]\Vert & = \left\Vert\sum_{h\in G:\left|p_{1}\circ p_{H}(h)\right|\leq N_{1}}(1\otimes\varphi_{hg}^{\ell})a_{h}\lambda_{hg}\right\Vert\\ & = \left\Vert\sum_{-N_{1}\leq i\leq N_{1}}\sum_{h\in\ker(p_{1}\circ p_{H})}(1\otimes\varphi_{hh_{i}g}^{\ell})a_{hh_{i}}\lambda_{hh_{i}g}\right\Vert\\ &= \left\Vert\sum_{-N_{1}\leq i\leq N_{1}}\mathbb{E}_{1}([1\otimes M_{\ell},x\lambda_{(h_{i}g)^{-1}}]\lambda_{h_{i}g})\right\Vert \\ & = \left\Vert\sum_{-N_{1}\leq i\leq N_{1}}\mathbb{E}_{1}([1\otimes M_{\ell},x]\lambda_{(h_{i}g)^{-1}})\lambda_{h_{i}g}\right\Vert\\ & \leq 2N_{1}+1, \end{align*} $$

and similarly,

$$\begin{align*}\Vert[D_{A}\otimes1,x_{1}]\Vert=\left\Vert\sum_{-N_{1}\leq i\leq N_{1}}\mathbb{E}_{1}([D_{A}\otimes1,x]\lambda_{(h_{i}g)^{-1}})\lambda_{h_{i}g}\right\Vert\leq2N_{1}+1. \end{align*}$$

In the same way, we can now apply $P_{2}$ to $[1\otimes M_{\ell },x_{1}]\lambda _{g^{-1}}$ and invoke Lemma 2.12 again to find $N_{2}\in \mathbb {N}$ with $\left \Vert x_{1}-x_{2}\right \Vert \leq m^{-1}\varepsilon $ , $\left \Vert [1\otimes M_{\ell },x_{2}]\right \Vert \leq (2N_{1}+1) (2N_{2}+1)$ and $\left \Vert [D_{A}\otimes 1,x_{1}]\right \Vert \leq (2N_{1}+1)(2N_{2}+1)$ , where $x_{2}:=\sum _{h\in H:\left |p_{1}\circ p_{H}(h)\right |\leq N_{1},\left |p_{2}\circ p_{H}(h)\right |\leq N_{2}} a_{h}\lambda _{hg}\in A\rtimes _{\alpha ,r}G$ . Performing these steps repeatedly leads to a sequence of natural numbers $N_{1},...,N_{m}\in \mathbb {N}$ and elements $x_{1},...,x_{m}\in A\rtimes _{\alpha ,r}G$ given by

$$\begin{align*}x_{i}:=\sum_{h\in H:\left|p_{1}\circ p_{H}(h)\right|\leq N_{1},...,\left|p_{i}\circ p_{H}(h)\right|\leq N_{i}}a_{h}\lambda_{hg} \end{align*}$$

for which $\left \Vert x_{i}{\kern-1pt}-{\kern-1pt}x_{i+1}\right \Vert {\kern-1pt}<{\kern-1pt}m^{-1}\varepsilon $ , $\left \Vert [1{\kern-1pt}\otimes{\kern-1pt} M_{\ell },x_{i}]\right \Vert {\kern-1pt}\leq{\kern-1pt} (2N_{1}{\kern-1pt}+{\kern-1pt}1)...(2N_{i}{\kern-1pt}+{\kern-1pt}1)$ and $\left \Vert [D_{A}\otimes 1,x_{i}]\right \Vert \leq (2N_{1}+1)...(2N_{i}+1)$ . For $i=m$ , we in particular have

$$\begin{align*}\left\Vert x-x_{m}\right\Vert \leq\left\Vert x-x_{1}\right\Vert +\left\Vert x_{1}-x_{2}\right\Vert +...+\left\Vert x_{m-1}-x_{m}\right\Vert <\varepsilon. \end{align*}$$

Set $\widetilde {N}:=\max \{N_{1},...,N_{m}\}$ and note that $p_{H}(\text {supp}(x_{m}\lambda _{g^{-1}}))$ is contained in the $\widetilde {N}$ -ball of $\mathbb {Z}^{m}$ with respect to the restriction of the supremum norm on $\mathbb {R}^{m}$ to $\mathbb {Z}^{m}$ . It follows that there exist elements $g_{1},...,g_{n}\in G$ with $\text {supp}(x_{m})\subseteq K:=\bigcup _{i=1}^{n}[H,H]g_{i}.$ We therefore get that $\mathcal {Q}_{2}^{g}\subseteq _{\varepsilon }(2N_{1}+1)...(2N_{m}+1)\mathcal {Q}_{2}^{g}\cap C_{c}(K,\mathcal {A})$ , which finishes the proof.

Proof For $g\in G$ , set $\mathcal {Q}_{g}{\kern-1pt}:={\kern-1pt}\left \{ x{\kern-1pt}\in{\kern-1pt} C_{c}(Hg,\mathcal {A})\mid \left \Vert [D_{A}{\kern-1pt}\otimes{\kern-1pt} 1,x]\right \Vert {\kern-1pt}\leq{\kern-1pt} 1\text { and }\left \Vert [1{\kern-1pt}\otimes{\kern-1pt} M_{\ell },x]\right \Vert {\kern-1pt}\leq{\kern-1pt} 1\right \} $ and write $\mathcal {Q}_{g}^{\prime }$ for the set of all elements $x=\sum _{h\in [H,H]}a_{h}\lambda _{hg}\in C_{c}(Hg,\mathcal {A})$ with $(a_{h})_{h\in [H,H]}\subseteq \mathcal {A}$ satisfying $\left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ and $\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1$ . The “only if” direction follows in the same way as in the proof of Lemma 2.8. For the “if” direction, assume that $\mathcal {Q}_{g}^{\prime }$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ for every $g\in G$ and let $\varepsilon>0$ . By Proposition 2.11, for fixed $g\in G$ , we find $\delta>0$ and finitely many elements $g_{1},...,g_{n}\in G$ such that $\mathcal {Q}_{g}\subseteq _{\varepsilon /4}\delta \mathcal {Q}_{g}\cap C_{c}(K,\mathcal {A})$ , where $K:=\bigcup _{i=1}^{n}[H,H]g_{i}$ . In other words, for every $x\in \mathcal {Q}_{g}$ , there exists $y\in \delta \mathcal {Q}_{g}$ of the form $y=\sum _{i=1}^{n}\sum _{h\in [H,H]}b_{hg_{i}}\lambda _{hg_{i}}$ with $b_{hg_{i}}\in \mathcal {A}$ for $h\in [H,H]$ , $i=1,...,n$ such that $\left \Vert x-y\right \Vert <\frac {\varepsilon }{4}$ . For every i, set $y_{i}:=\sum _{h\in [H,H]}b_{hg_{i}}\lambda _{hg_{i}}$ . By the same argument as in the proof of Lemma 2.8 and Proposition 2.11,

$$ \begin{align*} \left\Vert [1\otimes M_{\ell},y_{i}]\right\Vert & = \left\Vert\sum_{h\in[H,H]}(1\otimes\varphi_{hg_{i}})b_{hg_{i}}\lambda_{hg_{i}}\right\Vert\\ &= \Vert\mathbb{E}_{[H,H]}([1\otimes M_{\ell},y\lambda_{g_{i}^{-1}}]\lambda_{g_{i}})\Vert \\ & = \Vert[1\otimes M_{\ell},\mathbb{E}_{[H,H]}(y\lambda_{g_{i}^{-1}})\lambda_{g_{i}}]\Vert \\ & \leq \left\Vert [1\otimes M_{\ell},y]\right\Vert \\ & \leq \delta, \end{align*} $$

and similarly,

$$\begin{align*}\left\Vert [D_{A}\otimes1,y_{i}]\right\Vert =\Vert\mathbb{E}_{[H,H]}([D_{A}\otimes1,y]\lambda_{g_{i}^{-1}})\lambda_{g_{i}}\Vert\leq\Vert[D_{A}\otimes1,y]\Vert\leq\delta, \end{align*}$$

where $\mathbb {E}_{[H,H]}$ is the contractive linear map from Lemma 2.6. We conclude that $\mathcal {Q}_{g}\subseteq _{\varepsilon /4}\mathcal {R}$ , where $\mathcal {R}:=\delta \mathcal {Q}_{g_{1}}^{\prime }+...+\delta \mathcal {Q}_{g_{n}}^{\prime }$ . From our assumption, it can easily be derived that $\mathcal {R}$ has a totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . We hence find finitely many elements $x_{1},...,x_{m}\in \mathcal {R}$ such that for every $y\in \mathcal {R}$ , there exists $1\leq i\leq m$ with $\left \Vert (y-x_{i})+\mathbb {C}1\right \Vert <\frac {\varepsilon }{4}$ . For every i, choose $\widetilde {x}_{i}\in \mathcal {Q}_{g}$ with $\left \Vert (x_{i}-\widetilde {x}_{i})+\mathbb {C}1\right \Vert <\frac {\varepsilon }{2}$ , if possible. We claim that the $\varepsilon $ -balls around the $\widetilde {x}_{i}+\mathbb {C}1$ cover the image of $\mathcal {Q}_{g}$ in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . Indeed, for $x\in \mathcal {Q}_{g}$ , there exists $y\in \mathcal {R}$ with $\left \Vert x-y\right \Vert <\frac {\varepsilon }{4}$ , and we find i with $\left \Vert (y-x_{i})+\mathbb {C}1\right \Vert <\frac {\varepsilon }{4}$ . By $\left \Vert (x-x_{i})+\mathbb {C}1\right \Vert \leq \left \Vert (x-y)+\mathbb {C}1\right \Vert +\left \Vert (y-x_{i})+\mathbb {C}1\right \Vert <\frac {\varepsilon }{2},$ the element $\widetilde {x}_{i}\in \mathcal {Q}_{g}$ exists and

$$\begin{align*}\left\Vert (x-\widetilde{x}_{i})+\mathbb{C}1\right\Vert \leq\left\Vert (x-y)+\mathbb{C}1\right\Vert +\left\Vert (y-x_{i})+\mathbb{C}1\right\Vert +\left\Vert (x_{i}-\widetilde{x}_{i})+\mathbb{C}1\right\Vert <\varepsilon. \end{align*}$$

The claim follows. Hence, the image of $\mathcal {Q}_{g}$ in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ is totally bounded, and thus, by Lemma 2.8, the even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space.

For the proof of the second statement, assume that the derived subgroup $[H,H]$ is finite and fix $g\in G$ . We proceed by arguing along the lines of the proof of [Reference Hawkins, Skalski, White and Zacharias18, Theorem 2.11]. For $x=\sum _{h\in [H,H]}a_{h}\lambda _{hg}\in \mathcal {Q}_{g}^{\prime }$ with $(a_{h})_{h\in [H,H]}\subseteq \mathcal {A}$ , one has that for every $\xi ,\eta $ in the domain of $D_{A}$ and $h\in H$ ,

$$ \begin{align*} \left\langle [D_{A},a_{h}]\xi,\eta\right\rangle & = \left\langle (D_{A}\otimes1)x\lambda_{(hg)^{-1}}(\xi\otimes\delta_{e}),\eta\otimes\delta_{e}\right\rangle -\left\langle x\lambda_{(hg)^{-1}}(D_{A}\otimes1)(\xi\otimes\delta_{e}),\eta\otimes\delta_{e}\right\rangle \\ & = \left\langle [D_{A}\otimes1,x](\xi\otimes\delta_{(hg)^{-1}}),\eta\otimes\delta_{e}\right\rangle \end{align*} $$

and therefore, $\left \Vert [D_{A},a_{h}]\right \Vert \leq \left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ . Similarly, for $h\in H$ and $\xi ,\eta \in \mathcal {H}_{A}$ ,

$$\begin{align*}\left\langle [1\otimes M_{\ell},x](\xi\otimes\delta_{(hg)^{-1}}),\eta\otimes\delta_{e}\right\rangle =\left\langle x(1\otimes M_{\ell})(\xi\otimes\delta_{(hg)^{-1}}),\eta\otimes\delta_{e}\right\rangle =\ell(hg)\left\langle a_{h}\xi,\eta\right\rangle \end{align*}$$

so that $\left \Vert a_{h}\right \Vert \leq (\ell (hg))^{-1}\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq L$ for every $h\in [H,H]\setminus \{g^{-1}\}$ , where

$$\begin{align*}L:=\max\{(\ell(hg))^{-1}\mid h\in[H,H]\setminus\{g^{-1}\}\}. \end{align*}$$

It follows that $\mathcal {Q}_{g}^{\prime }$ is contained in the set of all $x=\sum _{h\in [H,H]}a_{h}\lambda _{hg}\in C_{c}(Hg,\mathcal {A})$ with $(a_{h})_{h\in [H,H]}\subseteq \mathcal {A}$ satisfying $\left \Vert [D_{A},a_{h}]\right \Vert \leq L^\prime $ for all $h\in H$ and $\left \Vert a_{h}\right \Vert \leq L^\prime $ for all $h\in [H,H]\setminus \{g^{-1}\}$ with $L^{\prime }:=\max \{1,L\}$ . Denote this set by $\mathcal {S}_{g}$ . We claim that $\mathcal {S}_{g}$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ , which then implies that $\mathcal {Q}_{g}^{\prime }$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ , and hence, by the previous part, that the triple $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space. Indeed, by Theorem 1.3, the set $F:=\{a\in \mathcal {A}\mid \left \Vert a\right \Vert \leq L^\prime \text { and }\left \Vert [D_{A},a]\right \Vert \leq L^\prime \}$ is totally bounded in A. For every $\varepsilon>0$ , we can hence pick a finite subset $F_{1}$ of F such that the $\frac {\varepsilon }{\#[H,H]}$ -balls around its elements cover F. Similarly, we can choose a finite subset $F_{2}$ of $\{a\in \mathcal {A}\mid \left \Vert [D_{A},a]\right \Vert \leq L^\prime \}$ such that the $\frac {\varepsilon }{\#[H,H]}$ -balls around the image of the elements of $F_{2}$ in $A/\mathbb {C}1$ covers the image of $\{a\in \mathcal {A}\mid \left \Vert [D_{A},a]\right \Vert \leq L^\prime \}$ . From this, we can deduce that if $g\in [H,H]$ , the image of

$$\begin{align*}\left\{ \sum_{h\in[H,H]}f_{h}\lambda_{hg}\mid f_{g^{-1}}\in F_{2}\text{ and }f_{h}\in F_{1}\text{ for }h\neq g^{-1}\right\} \end{align*}$$

is an $\varepsilon $ -net for the image of $\mathcal {S}_{g}$ in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ , and similarly, the image of

$$\begin{align*}\left\{ \sum_{h\in[H,H]}f_{h}\lambda_{hg}\mid f_{h}\in F_{1}\text{ for all }h\in[H,H]\right\} \end{align*}$$

is an $\varepsilon $ -net for the image of $\mathcal {S}_{g}$ in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ if $g\notin [H,H]$ . This finishes the proof.

2.3 The construction of odd spectral triples

In [Reference Hawkins, Skalski, White and Zacharias18, Subsection 2.4], it was noted that analogous to the construction of even spectral triples on crossed product C $^{\ast }$ -algebras coming from odd spectral triples, a similar procedure can be used to obtain odd spectral triples coming from even ones. As in Subsection 2.1, let $\alpha :G\rightarrow \text {Aut}(A)$ be an action of a discrete group G on a unital separable C $^{\ast }$ -algebra A and let $\ell :G\rightarrow \mathbb {R}_{+}$ be a proper length function on G. Assume that

$$\begin{align*}\left(\mathcal{A},\mathcal{H}_{A,1}\oplus\mathcal{H}_{A,2},\left(\begin{array}{cc} 0 & D_{A}\\ D_{A}^{\ast} & 0 \end{array}\right)\right) \end{align*}$$

is a spectral triple on A with $\mathbb {Z}_{2}$ -grading $\mathcal {H}_{A}:=\mathcal {H}_{A,1}\oplus \mathcal {H}_{A,2}$ and corresponding faithful representation $\pi :=\pi _{1}\oplus \pi _{2}$ . As before, consider the canonical odd spectral triple $(\mathbb {C}[G],\ell ^{2}(G),M_{\ell })$ on $C_{r}^{\ast }(G)$ , where $M_{\ell }$ denotes the multiplication operator $\delta _{g}\mapsto \ell (g)\delta _{g}$ for $g\in G$ . The reduced crossed product C $^{\ast }$ -algebra $A\rtimes _{\alpha ,r}G$ can be (faithfully) represented on $\mathcal {H}:=(\mathcal {H}_{A,1}\otimes \ell ^{2}(G))\oplus (\mathcal {H}_{A,2}\otimes \ell ^{2}(G))$ in a natural way. By assuming metric equicontinuity in the sense that $\alpha _{g}(\mathcal {A})\subseteq \mathcal {A}$ and $\sup _{g\in G}\Vert \pi _{1}(g.a)D_{A}-D_{A}\pi _{2}(g.a)\Vert <\infty $ for all $a\in \mathcal {A}$ , $g\in G$ , one can define an odd spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H},D)$ on $A\rtimes _{\alpha ,r}G$ , where

(2.3) $$ \begin{align} D:=\left(\begin{array}{cc} 1\otimes M_{\ell} & D_{A}\otimes1\\ D_{A}^{\ast}\otimes1 & -1\otimes M_{\ell} \end{array}\right). \end{align} $$

This triple is nondegenerate if the one on A is.

We claim that an analog to Theorem 2.13 holds in this setting as well. This follows from a variation of the characterization in Proposition 2.7.

Proposition 2.14 The even spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H},D)$ defined above is a spectral metric space if and only if the set of all elements $x=\sum _{g\in G}a_{g}\lambda _{g}\in C_{c}(G,\mathcal {A})\subseteq \mathcal {B}(\mathcal {H})$ with $(a_{g})_{g\in G}\subseteq \mathcal {A}$ for which the operator norms of the commutators

$$\begin{align*}\left[x,\left(\begin{array}{cc} 1\otimes M_{\ell} & 0\\ 0 & -1\otimes M_{\ell} \end{array}\right)\right],\left[x,\left(\begin{array}{cc} 0 & D_{A}\otimes1\\ D_{A}^{\ast}\otimes1 & 0 \end{array}\right)\right]\in\mathcal{B}(\mathcal{H}) \end{align*}$$

are bounded by $1$ , has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ .

Theorem 2.15 Let

$$\begin{align*}\left(\mathcal{A},\mathcal{H}_{A,1}\oplus\mathcal{H}_{A,2},\left(\begin{array}{cc} 0 & D_{A}\\ D_{A}^{\ast} & 0 \end{array}\right)\right) \end{align*}$$

be a nondegenerate even spectral triple on a separable unital C $^{\ast }$ -algebra A with $\mathbb {Z}_{2}$ -grading $\mathcal {H}_{A}:=\mathcal {H}_{A,1}\oplus \mathcal {H}_{A,2}$ and corresponding representation $\pi :=\pi _{1}\oplus \pi _{2}$ , and assume that the induced Lipschitz semi-norm $L_{D_{A}}(a):=\left \Vert [D_{A},a]\right \Vert ,a\in \mathcal {A}$ defines a compact quantum metric space $(A,L_{D_{A}})$ . Let further $\alpha :G\rightarrow \text {Aut}(A)$ be a metrically equicontinuous action of a finitely generated discrete group G equipped with a proper length function $\ell :G\rightarrow \mathbb {R}_{+}$ and assume that there exists a finite index subgroup H of G that is separated with respect to the restricted length function $\ell |_{H}$ . As before, define $\mathcal {H}:=(\mathcal {H}_{A,1}\otimes \ell ^{2}(G))\oplus (\mathcal {H}_{A,2}\otimes \ell ^{2}(G))$ and D as in (2.3). Then the odd spectral triple $(C_{c}(G,\mathcal {A}),\mathcal {H},D)$ is a spectral metric space if and only if for every $g\in G$ , the set of all elements $x=\sum _{h\in [H,H]}a_{h}\lambda _{hg}\in C_{c}(G,\mathcal {A})$ with $(a_{h})_{h\in [H,H]}\subseteq \mathcal {A}$ for which the operator norms of the commutators

$$\begin{align*}\left[x,\left(\begin{array}{cc} 1\otimes M_{\ell} & 0\\ 0 & -1\otimes M_{\ell} \end{array}\right)\right],\left[x,\left(\begin{array}{cc} 0 & D_{A}\otimes1\\ D_{A}^{\ast}\otimes1 & 0 \end{array}\right)\right] \end{align*}$$

are bounded by $1$ , has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ .

In particular, if $[H,H]$ is finite, then $(C_{c}(G,\mathcal {A}),\mathcal {H},D)$ is a spectral metric space.

Despite being lengthy, the arguments for proving Theorem 2.15 are essentially variations of those in Subsection 2.1 and Subsection 2.2. We therefore omit the details here.

3.1 Integer lattices

Recall that a quasi-isometric embedding between metric spaces $(X,d_{X})$ and $(Y,d_{Y})$ is a map $f:X\rightarrow Y$ for which there exists $C\geq 1$ and $r>0$ with

$$\begin{align*}C^{-1}d_{X}(x,y)-r\leq d_{Y}(f(x),f(y))\leq Cd(x,y)+r \end{align*}$$

for all $x,y\in X$ . It is well-known that, given finite generating sets $S=S^{-1}$ and $S^{\prime }=(S^\prime )^{-1}$ of a group G, the identity map on G equipped with the respective induced word metrics defines a quasi-isometric embedding. Similarly, if G is a finitely generated group and $H\leq G$ is a finite index subgroup, then H is also finitely generated, and the embedding of H into G is quasi-isometric with respect to the induced word metrics; this follows, for instance, from the Milnor-Svarc Lemma. We call two length functions $\ell ,\ell ^{\prime }:G\rightarrow \mathbb {R}_{+}$ on a group G bi-Lipschitz equivalent if the identity on G equipped with the metrics $d_{\ell }$ and $d_{\ell ^{\prime }}$ is a quasi-isometric embedding – that is, if there exist $C\geq 1$ and $r \geq 0$ with $C^{-1}\ell (g)-r\leq \ell ^{\prime }(g)\leq C\ell (g)+r$ for all $g\in G$ .

From now on, we restrict to the case of integer lattices $G=\mathbb {Z}^{m}$ , $m\in \mathbb {N}$ equipped with length functions $\ell :G\rightarrow \mathbb {R}_{+}$ . By applying Fekete’s Subadditivity Lemma, one obtains that for every $g\in G$ , the limit $\lim _{i\rightarrow \infty }i^{-1}\ell (ig)$ exists and that it coincides with $\inf _{i\in \mathbb {N}}i^{-1}\ell (ig)$ ; so in particular, $\lim _{i\rightarrow \infty }i^{-1}\ell (ig)\leq \ell (g)$ . The function $g\mapsto \lim _{i\rightarrow \infty }i^{-1}\ell (ig)$ uniquely extends to a semi-norm $\left \Vert \cdot \right \Vert _{\ell }$ on $\mathbb {R}^{m}$ , which is called the asymptotic semi-norm (or stable semi-norm) associated with $\ell $ ; see, for example, [Reference Burago, Burago and Ivanov6, Proposition 8.5.3]. In many interesting cases, the asymptotic semi-norm is positive definite (i.e., a genuine norm). This is, for instance, the case if $\ell $ is bi-Lipschitz equivalent to a word length function (e.g., if $\mathbb {Z}^{m}$ embeds as a finite index subgroup into a larger group and $\ell $ is a restricted word length function). Indeed, in that case, there exists a constant $C\geq 1$ such that

$$\begin{align*}C^{-1}\left\Vert x\right\Vert _{1}=C^{-1}\left\Vert x\right\Vert _{\ell_{1}}\leq\left\Vert x\right\Vert _{\ell}\leq C\left\Vert x\right\Vert _{\ell_{1}}=C\left\Vert x\right\Vert _{1} \end{align*}$$

for every $x\in \mathbb {R}^{m}$ . Here, $\left \Vert \cdot \right \Vert _{1}$ denotes the 1-norm on $\mathbb {R}^{m}$ , and $\ell _{1}$ is the word length function associated with the canonical generating set of $\mathbb {Z}^m$ .

The restriction $\ell ^{\text {as}}:\mathbb {Z}^{m}\rightarrow \mathbb {R}_{+}$ of the asymptotic semi-norm to $\mathbb {Z}^{m}$ is a homogeneous pseudo-length function. The proof of the following lemma is an easy exercise.

In general, there is no reason to expect that the sequence in Lemma 3.1 converges with respect to the operator norm (i.e., uniformly). Still, for many natural examples, that is the case.

As it turns out, $\ell ^{\text {as}}$ very naturally occurs in the context of the question for separateness of the pair $(G,\ell )$ .

Proof Let $\mu :\ell ^{\infty }(G)\rightarrow \mathbb {C}$ be an invariant mean. Then,

$$\begin{align*}\widehat{\mu}_{\ell}\circ p_{G}(g)-\widehat{\mu}_{\ell^{\text{as}}}\circ p_{G}(g)=\mu(i^{-1}(\varphi_{ig}^{\ell}-\varphi_{ig}^{\ell^{\text{as}}}))\rightarrow0 \end{align*}$$

for every $g\in G$ , and hence, $\widehat {\mu }_{\ell }=\widehat {\mu }_{\ell ^{\text {as}}}$ . This implies the claim.

By adding the assumption that the asymptotic semi-norm is positive definite, we obtain the following much stronger result. Before giving a proof, we pick up some of its implications.

Theorem 3.3 applies to many natural situations. If, for instance, $\ell $ is a word length function, it is easy to show that the map $G\rightarrow \mathbb {R}_{+}$ , $g\mapsto \left |\ell (g)-\left \Vert g\right \Vert _{\ell }\right |$ is bounded (see, for example, [Reference Duchin, Lelièvre and Mooney15, Lemma 3.5]), and hence, $i^{-1}(\varphi _{ig}^{\ell }-\varphi _{ig}^{\ell ^{\text {as}}})\rightarrow 0$ uniformly. The proof of the following more general statement relies on the results in [Reference Lebedeva, Ohta and Zolotov22], which are again in the spirit of Burago’s approach in [Reference Burago5]. Recall that an action of a group G on a metric space $(X,d)$ is called cocompact if the quotient space $X/G$ is compact. It is called properly discontinuous if each point admits a neighborhood satisfying the property that all nontrivial elements of G move the neighborhood outside itself. The metric space $(X,d)$ is geodesic if, given two points, there exists a path between them whose length equals the distance between the points. Here, the length of a path $c:[0,1]\rightarrow X$ is defined as the infimum over all sums $\sum _{i=1}^{k}d(c(t_{i-1}),c(t_{i}))$ , where $0\leq t_{0}\leq t_{1}...\le t_{k}\leq 1$ .

Proof For the first statement, recall that Fekete’s Subadditivity Lemma implies $\ell ^{\text {as}}(h)\leq \ell (h)$ for all $h\in \mathbb {Z}^{m}$ . By [Reference Lebedeva, Ohta and Zolotov22, Lemma 20], there further exists a constant $C\geq 0$ such that $2\ell (h)\leq \ell (2h)+C$ for every $h\in \mathbb {Z}^{m}$ . Inductively, we obtain that

$$ \begin{align*} \ell(h)\leq\frac{\ell(2h)}{2}+C\leq\frac{\ell(4h)}{4}+\frac{3C}{2}\leq...\leq\frac{\ell(2^{i}h)}{2^{i}}+\left(2-\frac{1}{2^{i-1}}\right)C \end{align*} $$

for all $h\in G$ , $i\in \mathbb {N}$ , and therefore, $\ell (h)\leq \ell ^{\text {as}}(h)+2C$ . But then

$$ \begin{align*} \left\Vert \frac{\varphi_{ig}^{\ell}-\varphi_{ig}^{\ell^{\text{as}}}}{i}\right\Vert \leq \sup_{h\in\mathbb{Z}^{m}}\left\{ \left|\frac{\ell(h)-\ell^{\text{as}}(h)}{i}\right|+\left|\frac{\ell(h-ig)-\ell^{\text{as}}(h-ig)}{i}\right|\right\} \leq\frac{4C}{i}\rightarrow0 \end{align*} $$

for $g\in G$ .

The asymptotic semi-norm associated with $\ell $ is further positive definite. Indeed, by [Reference Burago, Burago and Ivanov6, Theorem 8.3.19], the metric $(g,h)\mapsto d(g.x_{0},h.x_{0})$ on G is bi-Lipschitz equivalent to a word metric, and thus, $\ell $ is bi-Lipschitz equivalent to a word length function. Therefore, by our discussion above, $\left \Vert \cdot \right \Vert _{\ell }$ is positive definite and $\ell $ is proper. We deduce the statement of the first part of the corollary by invoking Theorem 3.3.

For the second statement, we argue as in [Reference Lebedeva, Ohta and Zolotov22, Corollary 23]. Consider G equipped with the word length metric $d_{\ell _S}$ . Then $(G,d_{\ell _S})$ is a proper geodesic metric space, and the action of $\mathbb {Z}^{m}$ on G via left translation is free, cocompact, and properly discontinuous. Choose elements $g_{1},...,g_{k}\in G$ with $G=\bigcup _{i=1}^{k}\mathbb {Z}^{m}g_{i}$ and $\mathbb {Z}^{m}g_{i}\neq \mathbb {Z}^{m}g_{j}$ for $i\neq j$ and define $F:G\rightarrow \mathbb {R}^{m}$ via $F(hg_{i}):=F(g_{i})+h$ for $h\in \mathbb {Z}^{m}$ , $1\leq i\leq k$ , where $F(g_{1}),...,F(g_{k})\in \mathbb {R}^{m}$ are chosen arbitrarily. Then F satisfies the conditions of the first part of the corollary, and hence, G is separated with respect to the restricted word length function $\ell _{S}|_{\mathbb {Z}^{m}}$ .

With Theorem 2.13 and Theorem 2.15 at hand, the Corollary 3.4 implies the following important fact. Of course, the statement holds for all orbit metrics as in Corollary 3.4.

Let us now turn to the proof of Theorem 3.3. Our argument requires Rieffel’s construction in [Reference Rieffel29, Section 7]. For a given norm $\left \Vert \cdot \right \Vert $ on $\mathbb {R}^{m}$ , write $\ell _{\Vert \cdot \Vert }$ for its restriction to $\mathbb {Z}^{m}$ ; this defines a length function that is bi-Lipschitz equivalent to the word length function $\ell _1$ from before. Let $v\in \mathbb {R}^{m}$ with $\left \Vert v\right \Vert =1$ be a smooth point in the sense that there exists exactly one functional $\sigma _{v}$ on $\mathbb {R}^{m}$ with $ \Vert \sigma _{v} \Vert =1=\sigma _{v}(v)$ ; for the background on tangent functionals, see [Reference Dunford and Schwartz16, Section V.9]. Then the geodesic ray $\mathbb {R}_{+}\ni t\mapsto tv$ determines a Busemann point $\mathfrak {b}_{v}$ in the horofunction boundary $\partial _{\Vert \cdot \Vert }\mathbb {R}^{m}$ , and by [Reference Rieffel29, Proposition 6.2] and [Reference Rieffel29, Proposition 6.3], this point is fixed under the action of $\mathbb {R}^{m}$ with $\Vert tv \Vert - \Vert tv-x \Vert \rightarrow \sigma _v(x)$ for every $x\in \mathbb {R}^{m}$ . By invoking a variation of Kronecker’s theorem (see [Reference Rieffel29, Lemma 7.2]), one finds an unbounded strictly increasing sequence $(t_{i})_{i\in \mathbb {N}_{\geq 1}}\subseteq \mathbb {R}_{+}$ such that for every $i\in \mathbb {N}_{\geq 1}$ , there exists $x_{i}\in \mathbb {Z}^{m}$ with $\left \Vert x_{i}-t_{i}v\right \Vert <i^{-1}$ . Set $t_{0}:=0$ , $x_{0}:=0$ , and define $\gamma :\{t_{i}\mid i\in \mathbb {N}\}\rightarrow \mathbb {Z}^{m}$ by $\gamma (t_{i}):=x_{i}$ . Then $\gamma $ is an almost geodesic ray that determines a Busemann point $\mathfrak {b}_{v}^{\prime }\in \partial _{\ell _{\Vert \cdot \Vert }}\mathbb {Z}^{m}$ . By [Reference Rieffel29, Proposition 7.4], this point is fixed under the action of $\mathbb {Z}^{m}$ and satisfies $\varphi _{g}^{\ell _{\Vert \cdot \Vert }}(\mathfrak {b}_{v}^{\prime })=\sigma _{v}(g)$ for every $g\in \mathbb {Z}^{m}$ .

Proof of Theorem 3.3

Following Proposition 3.2, it suffices to show that G is separated with respect to the length function $\ell ^{\text {as}}$ . As $\ell ^{\text {as}}$ is the restriction of the asymptotic (semi-)norm $\left \Vert \cdot \right \Vert _{\ell }$ , we may apply [Reference Rieffel29, Proposition 7.4] to find for every smooth point $v\in \mathbb {R}^{m}$ (with respect to the asymptotic semi-norm) with $\left \Vert v\right \Vert _{\ell }=1$ a point $\mathfrak {b}_{v}^{\prime }\in \partial _{\ell ^{\text {as}}}G$ that is fixed under the action of G with $\varphi _{g}^{\ell ^{\text {as}}}(\mathfrak {b}_{v}^{\prime })=\sigma _{v}(g)$ for every $g\in G$ . Evaluation in $\mathfrak {b}_{v}^{\prime }$ leads to a (multiplicative) G-invariant state $\nu _{v}$ on $C(\overline {G}^{\ell ^{\text {as}}})$ . Further, by the amenability of G, the linear map $\chi :C_{r}^{\ast }(G)\rightarrow \mathbb {C}$ defined by $\chi (\lambda _{g}):=1$ for $g\in G$ is bounded and multiplicative (see [Reference Brown and Ozawa3, Theorem 2.6.8]). Recall that Proposition 2.5 (in combination with Fell’s absorption principle; see [Reference Brown and Ozawa3, Proposition 4.1.7]) provides a canonical identification of $C(\overline {G}^{\ell ^{\text {as}}})\rtimes _{\beta ,r}G$ with the C $^{\ast }$ -subalgebra of $\mathcal {B}(\ell ^{2}(G))$ generated by $C_{r}^{\ast }(G)$ , $C_{0}(G)$ and the multiplication operators $\{\varphi _{g}^{\ell ^{\text {as}}}\mid g\in G\}$ . Via composing $\chi $ with the conditional expectation $C(\overline {G}^{\ell ^{\text {as}}})\rtimes _{\beta ,r}G\rightarrow C_{r}^{\ast }(G)$ , $f\lambda _{g}\mapsto \nu _{v}(f)\lambda _{g}$ for $f\in C(\overline {G}^{\ell ^{\text {as}}})$ , $g\in G$ and extending to $\mathcal {B}(\ell ^{2}(G))$ , we hence obtain a state that contains $C_{r}^{\ast }(G)$ in its multiplicative domain (see [Reference Brown and Ozawa3, Proposition 1.5.7]). It is thus invariant under the canonical action of G and restricts to an invariant mean $\mu _{v}:\ell ^{\infty }(G)\rightarrow \mathbb {C}$ with $\widehat {(\mu _{v})}_{\ell ^{\text {as}}}=\sigma _{v}|_{G}$ . To conclude the statement from the theorem, it hence suffices to prove that the span of all $\sigma _{v}|_G$ where $v\in \mathbb {R}^{m}$ is a smooth point of the unit sphere (with respect to $\Vert \cdot \Vert _\ell $ ), coincides with $\text {Hom}(G,\mathbb {R})$ . For this purpose, assume that the complement of the span is nonempty and denote the canonical orthonormal basis of $\mathbb {R}^{m}$ by $(e_{i})_{i=1,...,m}$ . Then there exists a nontrivial vector $\xi $ in the orthogonal complement (with respect to the canonical inner product on $\mathbb {R}^{m}$ ) of

$$\begin{align*}\text{Span}\{(\sigma_{v}(e_{i}))_{i=1,...,m}\in\mathbb{R}^{m}\mid v\in\mathbb{R}^{m}\text{ with }\left\Vert v\right\Vert _{\ell}=1\text{ smooth point}\}\subseteq\mathbb{R}^{m}. \end{align*}$$

But this means that $\sigma _{v}(\xi )=0$ for all smooth points $v\in \mathbb {R}^{m}$ of the unit sphere. With [Reference Rieffel29, Proposition 6.7], we conclude that $\xi =0$ in contradiction to our assumption that $\xi $ is nontrivial.

3.2 Nilpotent groups

Besides constructing fixed points in the horofunction boundary of $\mathbb {Z}^{m}$ , $m\in \mathbb {N}$ associated with length functions that are restrictions of norms on $\mathbb {R}^{m}$ , in [Reference Rieffel29, Section 8], Rieffel also constructed finite orbits of horofunction boundaries of $\mathbb {Z}^{m}$ associated with word length functions. The investigation of such points was later extended by Walsh in [Reference Walsh32] to nilpotent groups. He proved that for a given nilpotent group G finitely generated by a set S with $S=S^{-1}$ , there is one finite orbit associated with each facet of the polytope obtained by projecting S onto the torsion-free component of the Abelianization of G. The aim of this subsection is to discuss the implications of Walsh’s results in our context.

Let us review the construction in [Reference Walsh32] in more detail. The map $p_{G}$ from before gives a group homomorphism $G\rightarrow \mathbb {Z}^{m}$ , where m is the rank of $G/[G,G]$ . Again, view $\mathbb {Z}^{m}$ as embedded into $\mathbb {R}^{m}$ and consider the convex hull $K_{S}:=\text {conv}(p_{G}(S))$ . The set $K_{S}$ defines a polytope in $\mathbb {R}^{m}$ . Its proper faces of co-dimension $1$ are called facets. For such a facet F, consider the subset $V_{F}:=\{s\in S\mid p_{G}(s)\in F\}$ of S and write $\left \langle V_{F}\right \rangle $ for the (nilpotent) subgroup of G generated by $V_{F}$ . This subgroup has finite index in G. Further, by [Reference Walsh32, Section 4], one finds a word $w_{F}$ with letters in V such that the infinite reduced word $w_{F}w_{F}...$ defines a geodesic path in the Cayley graph of G with respect to S in the sense that each of the word’s prefixes are geodesic with respect to the word metric $d_{\ell _S}$ . By Theorem 1.5, this geodesic path gives a Busemann point $\xi _{F}\in \partial _{\ell _{S}}G$ in the horofunction boundary of G. The stabilizer of $\xi _{F}$ is given by $\left \langle V_{F}\right \rangle $ . But even more is true.

Let $\mathcal {F}$ be the (finite) set of facets of $K_{S}$ . Similar to [Reference Rieffel29, Section 8] (and similar to Subsection 3.1), every facet $F\in \mathcal {F}$ of $K_{S}$ is characterized by the fact that there exists a (unique) linear functional $\sigma _{F}$ on $\mathbb {R}^{m}$ with $\sigma _{F}\circ p_G(s)\leq 1$ for all $s\in S$ and $F=\text {conv}(\{p_{G}(s)\mid s\in S\text { with }\sigma _{F}\circ p_{G}(s)=1\})$ . Rieffel calls this the support functional of F.

Proof By [Reference Walsh32, Lemma 4.3], there exists $i_{0}\in \mathbb {N}$ such that for all $i\geq i_{0}$ , the element $h^{-1}w_{F}^{i}$ can be written as a product of elements of $V_{F}$ . As in the proof of [Reference Walsh32, Lemma 4.1], one deduced that $\left |h^{-1}w_{F}^{i}\right |=\sigma _{F}\circ p_{G}(h^{-1}w_{F}^{i})$ and $\left |w_{F}^{i}\right |=\sigma _{F}\circ p_{G}(w_{F}^{i})$ for $i\geq i_{0}$ so that

$$\begin{align*}\varphi_{h}(\xi_{F})=\lim_{i\rightarrow\infty}(\sigma_{F}\circ p_{G}(w_{F}^{i})-\sigma_{F}\circ p_{G}(h^{-1}w_{F}^{i}))=\sigma_{F}\circ p_{G}(h).\\[-34pt] \end{align*}$$

Lemma 3.7 implies that nilpotent groups equipped with word length functions contain finite index subgroups that satisfy a property that is close to being separated.

Proof For every $F\in \mathcal {F}$ , the group $\left \langle V_{F}\right \rangle $ has finite index in G, so $H:=\bigcap _{F\in \mathcal {F}}\left \langle V_{F}\right \rangle $ is a subgroup of finite index as well. The evaluation maps $\mathcal {G}(G,\ell _{S})\cong C(\overline {G}^{\ell _{S}})\rightarrow \mathbb {C}$ , $f\mapsto f(\xi _{F})$ with $F\in \mathcal {F}$ extend to H-invariant states on $\ell ^{\infty }(G)$ that we denote by $\mu _{F}$ . As in Lemma 2.9, one obtains that $(\widehat {\mu _{F}})_{H}:\text {im}(p_{H})\rightarrow \mathbb {R}$ given by $p_{H}(h)\mapsto \mu _{F}(\varphi _{h}^{\ell _{S}})$ is a well-defined group homomorphism. By Lemma 3.7,

$$\begin{align*}\widehat{(\mu_{F})}_{H}\circ p_{H}(h)=\mu_{F}(\varphi_{h}^{\ell_{S}})=\sigma_{F}\circ p_{G}(h) \end{align*}$$

for every $h\in H$ , and therefore, $\widehat {(\mu _{F})}_{H}\circ p_{H}=(\sigma _{F}\circ p_{G})|_{H}$ . Now, every group homomorphism $\mathbb {Z}^{m}\rightarrow \mathbb {R}$ canonically extends to $\mathbb {R}^{m}$ . Further, every group homomorphism in $\text {Hom}(\mathbb {R}^{m},\mathbb {R})$ can be written as a linear combination of support functionals $\sigma _{F}$ , $F\in \mathcal {F}$ . Indeed, assume that $\text {Hom}(\mathbb {R}^{m},\mathbb {R})\setminus \text {Span}\{\sigma _{F}\mid F\in \mathcal {F}\}$ is nonempty and denote the canonical orthonormal basis of $\mathbb {R}^{m}$ by $(e_{i})_{i=1,...,m}$ . Then there exists a nontrivial vector v in the orthogonal complement (with respect to the canonical inner product) of $\text {Span}\{(\sigma _{F}(e_{i}))_{i=1,...,m}\in \mathbb {R}^{m}\mid F\in \mathcal {F}\}\subseteq \mathbb {R}^{m}$ . Without loss of generality, we can assume that v is contained in some facet $F\in \mathcal {F}$ . But then

$$\begin{align*}1=\sigma_{F}(v)=\left\langle v,(\sigma_{F}(e_{i}))_{i=1,...,m}\right\rangle =0, \end{align*}$$

which is a contradiction. Hence, $\text {Span}\{\sigma _{F}\mid F\in \mathcal {F}\}=\text {Hom}(\mathbb {R}^{m},\mathbb {R})$ , as claimed. By using this, we obtain that every group homomorphism $H\rightarrow \mathbb {R}$ that vanishes on $H\cap [G,G]$ can be written as a linear combination of the maps $\widehat {(\mu _{F})}_{H}\circ p_{H}$ , $F\in \mathcal {F}$ .

It can be checked that the property in Proposition 3.8 allows to prove a variant of Proposition 2.11 and Theorem 2.13 for nilpotent groups. Since the following theorem does not lead to interesting new examples of quantum metric spaces and since the proof is similar to the one in Subsection 2.2, we leave the details to the reader.

Example 3.10 Consider the discrete Heisenberg group

$$\begin{align*}H_{3}:=\left\{ \left(\begin{array}{ccc} 1 & x & z\\ 0 & 1 & y\\ 0 & 0 & 1 \end{array}\right)\mid x,y,z\in\mathbb{Z}\right\} \end{align*}$$

and define elements

$$\begin{align*}a:=\left(\begin{array}{ccc} 1 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right),\hspace{1em}b:=\left(\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{array}\right),\hspace{1em}c:=\left(\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right). \end{align*}$$

The set $S:=\{a,a^{-1},b,b^{-1}\}$ generates $H_{3}$ . Let $\ell :=\ell _{S}$ be the corresponding word length function. The commutator subgroup of $H_{3}$ coincides with its center which is given by the cyclic group $\left \langle c\right \rangle \cong \mathbb {Z}$ . Let $(\mathcal {A},\mathcal {H}_{A},D_{A})$ , $L_{D_{A}}$ , $\alpha $ , $\mathcal {H}$ , and D be as in Theorem 3.9. Then the theorem implies that $(C_{c}(G,\mathcal {A}),\mathcal {H}\oplus \mathcal {H},D)$ is a spectral metric space if and only if for every $h\in H_{3}$ , the set of all elements $x=\sum _{i=0}^{\infty }a_{i}\lambda _{c^{i}h}\in C_{c}(H_{3},\mathcal {A})$ with $(a_{i})_{i\in \mathbb {N}}\subseteq \mathcal {A}$ satisfying $\left \Vert [D_{A}\otimes 1,x]\right \Vert \leq 1$ and $\left \Vert [1\otimes M_{\ell },x]\right \Vert \leq 1$ has totally bounded image in $(A\rtimes _{\alpha ,r}G)/\mathbb {C}1$ . It would be interesting to see if our methods can be extended to give an analog to Corollary 3.5 in this setting (or even for general nilpotent groups). However, $\ell (c^{i})=2\lceil 2\sqrt {|i|}\rceil $ for every $i\in \mathbb {N}$ by [Reference Blachère2]. From this, it can be deduced that every invariant mean $\ell ^{\infty }(\left \langle c\right \rangle )\rightarrow \mathbb {C}$ must vanish on the elements $\varphi _{g}^{\ell |_{\left \langle c\right \rangle }}$ , $g\in \left \langle c\right \rangle $ . The restriction of $\ell $ to $\left \langle c\right \rangle \cong \mathbb {Z}$ hence provides a natural example of a group and a length function on it that is not separated.

4.1 Actions on AF-algebras

We begin by reminding the reader of a general construction by Christensen and Ivan [Reference Christensen and Ivan9] that allows associating spectral metric spaces with AF-algebras. This construction was also employed in [Reference Hawkins, Skalski, White and Zacharias18, Subsection 3.3].

Recall that an AF-algebra is an inductive limit of a sequence of finite-dimensional C $^{\ast }$ -algebras. Given a unital AF-algebra A, let $(\mathcal {A}_{i})_{i\in \mathbb {N}}\subseteq A$ with $\mathcal {A}_{0}:=\mathbb {C}1$ and $A=\overline {\bigcup _{i\in \mathbb {N}}\mathcal {A}_{i}}$ be an increasing sequence of finite-dimensional C $^{\ast }$ -algebras and let $\phi $ be a faithful state on A. We call $(\mathcal {A}_{i})_{i\in \mathbb {N}}$ an AF-filtration. Write $\pi _{\phi }$ for the (faithful) GNS-representation of A associated with $\phi $ and denote the corresponding GNS-Hilbert space by $L^{2}(A,\phi )$ . We will further write $\Omega _{\phi }\in L^{2}(A,\phi )$ for the canonical cyclic vector. Using this data, one can define a sequence $(H_{i})_{i\in \mathbb {N}}$ of pairwise orthogonal finite-dimensional subspaces of $L^{2}(A,\phi )$ via $H_{0}:=\pi _{\phi }(A_{0})\Omega _{\phi }=\mathbb {C}\Omega _{\phi }$ and $H_{i}:=\pi _{\phi }(A_{i})\Omega _{\phi }\cap (\pi _{\phi }(A_{i-1})\Omega _{\phi })^{\perp }$ for $i\in \mathbb {N}_{\geq 1}$ . Write $Q_{i}$ , $i\in \mathbb {N}$ for the orthogonal projection onto $H_{i}$ . As was argued in [Reference Christensen and Ivan9, Theorem 2.1], there exists a sequence $(\alpha _{i})_{i\in \mathbb {N}}$ of real numbers with $\alpha _{0}=0$ and $|\alpha _{i}|\rightarrow \infty $ such that the odd spectral triple $(\mathcal {A},L^{2}(A,\phi ),D)$ with $\mathcal {A}:=\bigcup _{i\in \mathbb {N}}A_{i}$ and $D:=\sum _{i\in \mathbb {N}}\lambda _{i}Q_{i}$ is a spectral metric space.

Now assume that $\alpha :G\rightarrow \text {Aut}(A)$ is an action of a discrete group G on A, satisfying $\alpha _{g}(A_{i})\subseteq A_{i}$ for every $g\in G$ , $i\in \mathbb {N}$ . Since the elements of $A_{i}$ commute with the projections $Q_{j}$ for $j>i$ , we obtain that for $x\in A_{i}$ ,

$$\begin{align*}\sup_{g\in G}\Vert[D,\alpha_{g}(x)]\Vert=\sup_{g\in G}\left\Vert\sum_{j\leq i}\lambda_{j}[Q_{j},\alpha_{g}(x)]\right\Vert\leq\sum_{j\leq i}2\left|\lambda_{j}\right|\Vert x\Vert < \infty; \end{align*}$$

that is, the action $\alpha $ is metrically equicontinuous. In particular, if G is a virtually Abelian group that is finitely generated by a set S with $S=S^{-1}$ and if $\ell :G\rightarrow \mathbb {R}_{+}$ is the corresponding word length function (or more generally a length function as in Corollary 3.4), we obtain from Corollary 3.5 a spectral metric space on the crossed product $A\rtimes _{r,\alpha }G$ .

Example 4.1 Let G be a countable residually finite discrete group and let $(G_{i})_{i\in \mathbb {N}}$ be a strictly decreasing sequence of finite index subgroups of G with $\bigcap _{i\in \mathbb {N}}G_{i}=\{e\}$ . For every $i\in \mathbb {N}$ , the group G acts on $G/G_{i}$ via left multiplication. Let $p_{i}:G/G_{i+1}\rightarrow G/G_{i}$ be the (surjective and G-equivariant) map $gG_{i+1}\mapsto gG_{i}$ and consider the corresponding inverse limit X given by

$$\begin{align*}X:=\{(g_{i})_{i\in\mathbb{N}}\mid p_{i}(g_{i+1})=g_{i}\text{ for all }i\geq0\}\subseteq\prod_{i\in\mathbb{N}}G/G_{i}. \end{align*}$$

We equip X with the subspace topology of the product $\prod _{i\in \mathbb {N}}G/G_{i}$ , where each $G/G_{i}$ , $i\in \mathbb {N}$ carries the discrete topology. In this way, X becomes a Cantor set, and the action of G on its left cosets extends to a continuous action on X that (following [Reference Cortez and Petite13, Definition 2]; see also [Reference Krieger21]) we call a G-subodometer action. The commutative C $^{\ast }$ -algebra $C(X)$ identifies with the inductive limit $\lim _{\rightarrow }(C(G/G_{i}),\iota _{i})$ , where $\iota _{i}:C(G/G_{i})\rightarrow C(G/G_{i+1})$ is given by $f\mapsto f\circ p$ ; so in particular, $C(X)$ is an AF-algebra. By fixing a faithful state $\phi $ on $A:=C(X)$ and by setting $\mathcal {A}_{i}:=C(G/G_{i})$ for $i\in \mathbb {N}$ , we can apply the construction from above to obtain a spectral metric space $(\mathcal {A},L^{2}(C(X),\phi ),D)$ on $C(X)$ . In particular, if G is a virtually Abelian group that is finitely generated by a set S with $S=S^{-1}$ and if $\ell :G\rightarrow \mathbb {R}_{+}$ is the corresponding word length function (or more generally a length function as in Corollary 3.4), we obtain a spectral metric space on $C(X)\rtimes _{r,\alpha }G$ . The crossed product $C(X)\rtimes _{r,\alpha }G$ is called a generalized Bunce-Deddens algebra (see [Reference Orfanos23] and [Reference Carrión7]); note that for $G=\mathbb {Z}$ and $G_{i}:=(m_{1}...m_{i})\mathbb {Z}\subseteq \mathbb {Z}$ where $(m_{i})_{i\in \mathbb {N}}$ is a sequence of natural numbers with $m_{i}\geq 2$ for all $i\in \mathbb {N}$ , we recover the classical Bunce-Deddens algebras (see [Reference Bunce and Deddens4] and also [Reference Davidson14, Chapter V.3]).

4.2 Higher-dimensional noncommutative tori

The rotation algebra (or noncommutative 2-torus) $\mathcal {A}_{\theta }$ , $\theta \in \mathbb {R}$ , introduced in [Reference Rieffel25], can be defined as the universal C $^{\ast }$ -algebra generated by two unitaries u and v subject to the relation $uv=e^{2\pi i\theta }vu$ . In the case where $\theta \in \mathbb {Z}$ , $\mathcal {A}_{\theta }\cong C(\mathbb {T}^{2})$ and for irrational values of $\theta $ , the C $^{\ast }$ -algebra $\mathcal {A}_{\theta }$ is simple. The construction admits a natural generalization to higher dimensions: let $\Theta :=(\theta _{i,j})_{i,j=1,...,m}$ be a skew symmetric real $(m\times m)$ -matrix (i.e., $\theta _{i,j}=-\theta _{j,i}$ for all $1\leq i,j\leq m$ ) and define $\mathcal {A}_{\Theta }$ to be the universal C $^{\ast }$ -algebra generated by unitaries $u_{1},...,u_{m}$ subject to relations $u_{i}u_{j}=e^{2\pi i\theta _{i,j}}u_{j}u_{i}$ for $1\leq i,j\leq m$ . These C $^{\ast }$ -algebras, which were defined in [Reference Rieffel26], are called noncommutative m-tori. Note that for $m=1$ , the C $^{\ast }$ -algebra $\mathcal {A}_{\Theta }$ is isomorphic to $C(\mathbb {T})$ , and for $m=2$ , we have $\mathcal {A}_{\Theta }=\mathcal {A}_{\theta _{1,2}}$ .

Any noncommutative torus can be constructed as an iteration of crossed products by actions of the integers $\mathbb {Z}$ . To make this precise, set $\Theta _{d}:=(\theta _{i,j})_{1\leq i,j\leq d}$ for $d=1,...,m$ and define an action

$$\begin{align*}\alpha_{d}:\mathbb{Z}\curvearrowright\mathcal{A}_{\Theta_{d}}\text{ via }\alpha_{d}^n(u_{i}):=e^{-2\pi in\theta_{i,d+1}}u_{i}, \end{align*}$$

where the $u_{1},...,u_{d}$ are the standard generators of $\mathcal {A}_{\Theta _{d}}$ . Write $\widetilde {u}_{1},...,\widetilde {u}_{d-1}$ for the standard generators of $\mathcal {A}_{\Theta _{d-1}}$ . Then there exists an isomorphism $\mathcal {A}_{\Theta _{d}}\cong \mathcal {A}_{\Theta _{d-1}}\rtimes _{\alpha _{d-1},r}\mathbb {Z}$ defined by $u_{i}\mapsto \widetilde {u}_{i}$ for $i=1,...,d-1$ and $u_{d}\mapsto \lambda _{1}$ . We obtain that

$$\begin{align*}\mathcal{A}_{\Theta}\cong(...((\mathcal{A}_{\Theta_{1}}\rtimes_{\alpha_{1}}\mathbb{Z})\rtimes_{\alpha_{2}}\mathbb{Z})...)\rtimes_{\alpha_{m-1}}\mathbb{Z}\cong(...((C(\mathbb{T})\rtimes\mathbb{Z})\rtimes\mathbb{Z})...)\rtimes\mathbb{Z}, \end{align*}$$

where the induced action of $\mathbb {Z}$ on $\mathbb {T}$ is given by rotation by the angle $\theta _{1,1}$ . Endow $C(\mathbb {T})$ with the canonical nondegenerate odd spectral triple $(C^{\infty }(\mathbb {T}),L^{2}(\mathbb {T}),D)$ , where D is the differentiation operator. We claim that, if we equip the integers with word length functions (or more generally length functions as in Corollary 3.4), a repeated application of Corollary 3.5 leads to spectral metric spaces on the noncommutative m-tori. Since it is well-known that the spectral triple $(C^{\infty }(\mathbb {T}),L^{2}(\mathbb {T}),D)$ on $\mathcal {A}_{\Theta _{1}}\cong C(\mathbb {T})$ is metric, for this, it suffices to prove that for every $d=1,...,m-1$ , the action $\alpha _{d}:\mathbb {Z}\curvearrowright \mathcal {A}_{\Theta _{d}}$ is metrically equicontinuous. This can be proved via induction over d: