Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nijenhuis, Albert
1959.
A Note on Hyperconvexity in Riemannian Manifolds.
Canadian Journal of Mathematics,
Vol. 11,
Issue. ,
p.
576.
Jänich, Klaus
1965.
Vektorraumbündel und der Raum der Fredholm-Operatoren.
Mathematische Annalen,
Vol. 161,
Issue. 2,
p.
129.
Bessaga, Czeslaw
and
Klee, Victor
1966.
Every non-normable Frechet space is homeomorphic with all of its closed convex bodies.
Mathematische Annalen,
Vol. 163,
Issue. 2,
p.
161.
Palais, Richard S.
1966.
Homotopy theory of infinite dimensional manifolds.
Topology,
Vol. 5,
Issue. 1,
p.
1.
Wood, R.
1966.
Banach algebras and Bott periodicity.
Topology,
Vol. 4,
Issue. 4,
p.
371.
Karoubi, Max
1970.
Séminaire Heidelberg-Saarbrücken-Strasbourg sur la K-Théorie.
Vol. 136,
Issue. ,
p.
66.
Karoubi, Max
1970.
Espaces classifiants en 𝐾-théorie.
Transactions of the American Mathematical Society,
Vol. 147,
Issue. 1,
p.
75.
Michael, E.
1970.
Set-Valued Mappings, Selections and Topological Properties of 2x.
Vol. 171,
Issue. ,
p.
54.
Chapman, T.A.
1971.
Deficiency in infinite-dimensional manifolds.
General Topology and its Applications,
Vol. 1,
Issue. 3,
p.
263.
Srinivasacharyulu, Kilambi
1971.
Deformations of some ?-structures.
Mathematische Zeitschrift,
Vol. 123,
Issue. 1,
p.
56.
Henderson, David.W.
1971.
Corrections and extensions of two papers about infinite-dimensional manifolds.
General Topology and its Applications,
Vol. 1,
Issue. 4,
p.
321.
Geoghegan, Ross
1972.
On spaces of homeomorphisms, embeddings and functions—I.
Topology,
Vol. 11,
Issue. 2,
p.
159.
Terry, Wesley E.
1974.
Conditions for a TVS to be homeomorphic with its countable product.
Transactions of the American Mathematical Society,
Vol. 190,
Issue. 0,
p.
233.
Smith, Harvey A.
1975.
Characteristic principal bundles.
Transactions of the American Mathematical Society,
Vol. 211,
Issue. 0,
p.
365.
Cattaneo, U.
1977.
On locally continuous cocycles.
Reports on Mathematical Physics,
Vol. 12,
Issue. 1,
p.
125.
Curtis, D.W.
and
Vo-Thanh-Liem
1979.
Infinite products which are homeomorphic to Hilbert space.
General Topology and its Applications,
Vol. 10,
Issue. 1,
p.
19.
Cattaneo, U.
1980.
Abelian extensions of topological vector groups.
Journal of Functional Analysis,
Vol. 35,
Issue. 2,
p.
143.
McClendon, J. F.
1982.
Fixed points of subopen multifunctions.
Proceedings of the American Mathematical Society,
Vol. 84,
Issue. 3,
p.
425.
Schröder, H.
1984.
On the homotopy type of the regular group of aW *-algebra.
Mathematische Annalen,
Vol. 267,
Issue. 2,
p.
271.
Corach, Gustavo
and
Suárez, Fernando Daniel
1985.
Extension problems and stable rank in commutative Banach algebras.
Topology and its Applications,
Vol. 21,
Issue. 1,
p.
1.
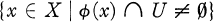 is open in X. Our purpose in these papers is to find conditions for the existence and extendability of selections.
is open in X. Our purpose in these papers is to find conditions for the existence and extendability of selections.