Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T09:39:07.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Construction of Primitives of Generalized Derivatives with Applications to Trigonometric Series

Published online by Cambridge University Press:  20 November 2018

P. S. Bullen
P. S. Bullen*
Affiliation:
University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is an extension of the ideas discussed in (3, §§ 14-16); the extension consisting of the use of the third and fourth symmetric Riemann derivative instead of the Schwarz or second symmetric Riemann derivative.

The J2integral, due to James (1), is defined in (3) as follows. Let f(x) be measurable on [a, b] and finite at each point; if there exists a continuous function F(x) such that D2F = f everywhere on (a, b),

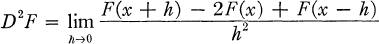
then

1.1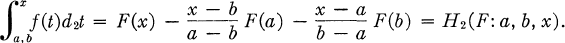

The definition is unique since if F(x) and G(x) are continuous and D2F =D2G everywhere then

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 48 - 58
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. James, R. D., A generalized integral II, Can. J. Math., 3 (1950), 297–306.Google Scholar
2. James, R. D., Summable trigonometric series, Pac. J. Math., 6 (1956), 99–110.Google Scholar
3. Jeffery, R. L., Trigonometric series (Toronto, 1956).Google Scholar
4. Kassimatis, C., Functions which have generalized Riemann derivatives, Can. J. Math., 3 (1958), 413–420.Google Scholar
5. Saks, S., On the generalized derivative, J. London Math. Soc, 7 (1932), 247–251.Google Scholar
6. Verblunsky, S., The generalized third derivative and its application to the theory of trigonometric series, Proc. London Math. Soc. (2), 31 (1930), 387–406.Google Scholar
7. Verblunsky, S., The generalized fourth derivative, J. London Math. Soc, 6 (1931), 82–84.Google Scholar
8. Zygmund, A., Trigonometric series (2nd éd.; Cambridge, 1959) I, II.Google Scholar