Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T01:09:06.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Composition of Inner Functions

Published online by Cambridge University Press:  20 November 2018

J. Mashreghi  and
M. Shabankhah
J. Mashreghi
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec, QC, Canada G1K 7P4.. e-mail: [email protected]
M. Shabankhah
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec, QC, Canada G1K 7P4.. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the image of the model subspace 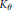${{K}_{\theta }}$ under the composition operator 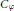${{C}_{\varphi }}$, where 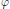$\varphi $ and 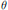$\theta $ are inner functions, and find the smallest model subspace which contains the linear manifold ${{C}_{\varphi }}{{K}_{\theta }}$. Then we characterize the case when 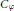${{C}_{\varphi }}$ maps 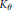${{K}_{\theta }}$ into itself. This case leads to the study of the inner functions 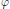$\varphi $ and 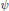$\psi $ such that the composition 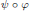$\psi \,\text{o}\,\varphi $ is a divisor of 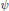$\psi $ in the family of inner functions.

Keywords

30D5530D0547B33composition operatorsinner functionsBlaschke productsmodel subspaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 387 - 399
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Beurling, A., On two problems concerning linear transformations in Hilbert space. Acta Math. 81(1949), 239–255.Google Scholar
[2] Chen, H. and Gauthier, P., Composition operators of μ-Bloch spaces. Canad. J. Math. 61(2009), 50–75. http://dx.doi.org/10.4153/CJM-2009-003-1 Google Scholar
[3] Cowen, C., Iteration and the solution of functional equations for functions analytic in the unit disk. Trans. Amer. Math. Soc. 265(1981), 69–95. http://dx.doi.org/10.1090/S0002-9947-1981-0607108-9 Google Scholar
[4] Cowen, C. and MacCluer, B. D., Composition operators on spaces of analytic functions. Stud. Adv. Math. CRC Press, Boca Raton, FL, 1995.Google Scholar
[5] Douglas, R. G., Shapiro, H. S. and Shields, A. L., Cyclic vectors and invariant subspaces for the backward shift operator. Ann. Inst. Fourier (Grenoble) 20(1970), fasc. 1, 37–76. http://dx.doi.org/10.5802/aif.338 Google Scholar
[6] Gallardo-Gutiérrez, Eva A. and González, Maria J., Exceptional sets and Hilbert–Schmidt composition operators. J. Funct. Anal. 199(2003) 287–300. http://dx.doi.org/10.1016/S0022-1236(02)00006-X Google Scholar
[7] Gallardo-Gutiérrez, Eva A., Hausdorff measures, capacities and compact composition operators. Math. Z. 253(2006), 63–74. http://dx.doi.org/10.1007/s00209-005-0878-6 Google Scholar
[8] Frostman, O., Sur les produits de Blaschke. (French) Kungl. Fysiografiska Sällskapets i Lund Förhandlingar [Proc. Roy. Physiog. Soc. Lund] 12(1942), 169–182.Google Scholar
[9] MacCluer, B., Compact composition operators in Hp(BN). Michigan Math. J. 32(1985), 237–248. http://dx.doi.org/10.1307/mmj/1029003191 Google Scholar
[10] Mashreghi, J., Representation Theorems in Hardy Spaces. London Math. Soc. Stud. Texts 74, Cambridge University Press, 2009.Google Scholar
[11] Mashreghi, J. and Shabankhah, M., Composition operators on finite rank model subspaces. Glasgow Math. J. 55(2013), 69–83.Google Scholar
[12] Shapiro, J. H., The essential norm of a composition operators. Ann. of Math. 125(1987), 375–404. http://dx.doi.org/10.2307/1971314 Google Scholar
[13] Shapiro, J. H., Composition Operators and Classical Function Theory. Universitext Tracts Math., Springer-Verlag, 1993.Google Scholar
[14] Tjani, M., Compact composition operators on Besov spaces. Trans. Amer. Math. Soc. 355(2003), 4683–4698. http://dx.doi.org/10.1090/S0002-9947-03-03354-3 Google Scholar
[15] Zorboska, N., Composition operators on weighted Dirichlet spaces. Proc. Amer. Math. Soc. 126(1998), 2013–2023. http://dx.doi.org/10.1090/S0002-9939-98-04266-X Google Scholar