Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T01:59:55.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness Properties of Carleman and Hille-Tamarkin Operators

Published online by Cambridge University Press:  20 November 2018

Anton R. Schep
Anton R. Schep*
Affiliation:
University of South Carolina, Columbia, South Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study integral operators with domain a Banach function space Lρ1 and range another Banach function space Lρ2 or the space L0 of all measurable functions. Recall that a linear operator T from Lρ1 into L0 is called an integral operator if there exists a μ × v-measurable function T(x, y) on X × Y such that

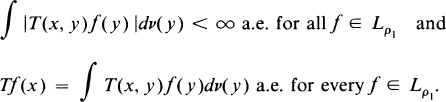
Such an integral operator is called a Carleman integral operator if for almost every x ∊ X the function

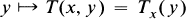
is an element of the associate space L′ρ1, i.e.,

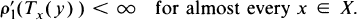
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 5 , 01 October 1985 , pp. 921 - 933
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Gretsky, N. and Uhl, J. J., Carleman and Korotkov operators on Banach spaces, Acta Sci. Math. 43 (1981), 111–119.Google Scholar
2. Luxemburg, W. A. J. and Zaanen, A. C., Riesz spaces I (North-Holland Publ. Comp., Amsterdam, 1971).Google Scholar
3. Schaefer, H. H., Banach lattices and positive operators, Grundl. Math. Wiss. 215 (Springer, Heidelberg, Berlin, New York, 1974).CrossRefGoogle Scholar
4. Schaefer, H. H. and Schlotterbeck, U., On the approximation of kernel operators by operators of finite rank, J. of Approx. Th. 13 (1975), 33–39.Google Scholar
5. Schep, A. R., Kernel operators, Indag. Math. 41 (1979), 39–53.Google Scholar
6. Schep, A. R., Generalized Carleman operators, Indag Math 42 (1980), 49–59.Google Scholar
7. Schep, A. R., Compactness properties of an operator which imply that it is an integral operator, T.A.M.S. 265 (1981), 111–119.Google Scholar
8. Zaanen, A. C., Integration (North-Holland Publ. Comp., Amsterdam, 1967).Google Scholar
9. Zaanen, A. C., Riesz spaces II (North-Holland Publ. Comp., Amsterdam, 1983).Google Scholar