Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-06T14:00:13.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Groups of Operators on Subproportional Quotients of l1m

Published online by Cambridge University Press:  20 November 2018

Piotr Mankiewicz
Piotr Mankiewicz*
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Śniadeckich 8, 00-950 Warsaw, Poland email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that a “typical” $n$-dimensional quotient 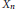${{X}_{n}}$ of 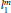$l_{1}^{m}$ with 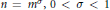$n={{m}^{\sigma }},0<\sigma <1$, has the property

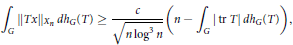$$\text{Average}\int_{G}{||Tx|{{|}_{{{X}_{n}}}}d{{h}_{G}}(T)\ge \frac{c}{\sqrt{n{{\log }^{3}}n}}\left( n-\int_{G}{|trT|d{{h}_{G}}(T)} \right)},$$

for every compact group 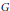$G$ of operators acting on 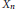${{X}_{n}}$, where 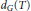${{d}_{G}}(T)$ stands for the normalized Haar measure on 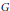$G$ and the average is taken over all extreme points of the unit ball of 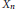${{X}_{n}}$. Several consequences of this estimate are presented.

Keywords

46B2046B09
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 5 , 01 October 2000 , pp. 999 - 1017
Copyright
Copyright © Canadian Mathematical Society 2000

References

[B] Ball, K., Normed spaces with a weak-Gordon-Lewis property. In: Functional Analysis, Springer Lecture Notes in Math. 1470(1991), 36–47.Google Scholar
[BKPS] Billard, P., Kwapień, S., A. Pełczyński and Ch. Samuel, Biorthogonal systems of random unconditional convergence in Banach spaces. Longhorn Notes, The University of Texas at Austin, 1986. 13–35.Google Scholar
[BP] Ball, K. and Pajor, A., Convex bodies with few faces. Proc. Amer. Math. Soc. 110(1990), 225–231.Google Scholar
[B1] Bourgain, J., Real isomorphic complex spaces need not to be complex isomorphic. Proc. Amer. Math. Soc. 96(1986), 221–226.Google Scholar
[B2] Bourgain, J., On finite dimensional homogenous Banach spaces. In: Geometric Aspects of Functional Analysis, Israel Seminar (eds. Lindenstrauss, J. and Milman, V. D.), Springer Lecture Notes in Math. 1317(1988), 232–239.Google Scholar
[G1] Gluskin, E. D., The diameter of Minkowski compactum roughly equals to n. (Russian) Funktsional. Anal. i Priloˇzen. 15(1981), 72–73.(English transl.: Funct. Anal. Appl. 15(1981), 57–58).Google Scholar
[G2] Gluskin, E. D., Finite-dimensional analogues of spaces without a basis. (Russian) Dokl. Acad. Nauk SSSR 261(1981), 1046–1050.Google Scholar
[GG] Garling, D. J. H. and Gordon, Y., Relations between some constants associated with finite-dimensional Banach spaces. Israel J. Math. 9(1971), 346–361.Google Scholar
[M1] Mankiewicz, P., Finite dimensional Banach spaces with symmetry constant of order Rn. Studia Math. 79(1984), 193–200.Google Scholar
[M2] Mankiewicz, P., Subspace mixing properties of operators in Rn with applications to Gluskin spaces. Studia Math. 88(1988), 51–67.Google Scholar
[M3] Mankiewicz, P., Compact groups of operators on proportional quotients of ln1. Israel J. Math. 109(1999), 75–91.Google Scholar
[MT1] Mankiewicz, P., Mankiewicz, P. and Tomczak-Jaegermann, N., A solution of the finite-dimensional homogeneous Banach spaces problem. Israel J. Math. 75(1991), 129–159.Google Scholar
[MT2] Mankiewicz, P., Schauder bases in quotients of subspaces of l2(X). Amer. J. Math. 116(1994), 1341–1363.Google Scholar
[MT3] Mankiewicz, P., Structural properties of weak cotype 2 spaces. Canad. J. Math. 48(1996), 607–624.Google Scholar
[MT4] Mankiewicz, P., Quotients of finite-dimensional Banach spaces; random phenomena. Handbook of geometry of Banach spaces, Elsevier Publ., to appear.Google Scholar
[P] Pisier, G., Volumes of Convex Bodies and Banach Spaces Geometry. Cambridge Univ. Press, 1989.Google Scholar
[S1] Szarek, S. J., The finite dimensional basis problem with an appendix on nets of Grassmann manifolds. Acta Math. 151(1983), 153–179.Google Scholar
[S2] Szarek, S. J., On the existence and uniqueness of complex structure and spaces with “few” operators. Trans. Amer.Math. Soc. 293(1986), 339–353.Google Scholar
[T] Tomczak-Jaegermann, N., Banach-Mazur Distances and Finite Dimensional Operator Ideals. Pitman Monographs Surveys Pure Appl. Math. 38, Longman Scientific & Technical, Harlow, and John Wiley, New York, 1989.Google Scholar