Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:43:45.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact 16-Dimensional Projective Planes with Large Collineation Groups. IV

Published online by Cambridge University Press:  20 November 2018

Helmut Salzmann
Helmut Salzmann*
Affiliation:
Universität Tübingen, Tubingen, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 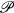be a topological projective plane with compact point set P of finite (covering) dimension. In the compact-open topology (of uniform convergence), the group Σ of continuous collineations of 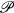is a locally compact transformation group of P.

THEOREM. If dim Σ > 40, then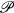is isomorphic to the Moufang plane 6 over the real octonions (and dim Σ = 78).

By [3] the translation planes with dim Σ = 40 form a one-parameter family and have Lenz type V. Presumably, there are no other planes with dim Σ = 40, cp. [17].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 4 , 01 August 1987 , pp. 908 - 919
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Bourbaki, N., Groupes et algèbres de Lie, 2nd ed. (Hermann, Paris, 1971).Google Scholar
2. Freudenthal, H. and de Vries, H., Linear Lie groups (Academic Press, New York, 1969).Google Scholar
3. Hàhl, H., Zur Klassifikation von 8-und 16-dimensionalen Translationsebenen nach ihren Kollineationsgruppen, Math. Z. 159 (1978), 259–294.Google Scholar
4. Hàhl, H., Homologies and dations in compact, connected projective planes, Topol. Appl. 12 (1981), 49–63.Google Scholar
5. Lôwen, R., Topology and dimension of stable planes: On a conjecture of H. Freudenthal, J. Reine Angew. Math. 343 (1983), 108–122.Google Scholar
6. Lôwen, R. and Salzmann, H., Collineation groups of compact connected projective planes, Arch. Math. 38 (1982), 368–373.Google Scholar
7. Poncet, J., Groupes de Lie compacts de transformations de l'espace euclidien et les sphères comme espaces homogènes, Comment. Math. Helv. 33 (1959), 109–120.Google Scholar
8. Salzmann, H., Kompakte zweidimensionale projektive Ebenen, Math. Ann. 145 (1962), 401–428.Google Scholar
9. Salzmann, H., Topological planes, Advances Math. 2 (1967), 1–60.Google Scholar
10. Salzmann, H., Kollineationsgruppen kompakter 4-dimensionaler Ebenen. II, Math. Z. 121 (1971), 104–110.Google Scholar
11. Salzmann, H., Compact 8-dimensional projective planes with large collineation groups, Geom. Dedic. 5 (1979), 139–161.Google Scholar
12. Salzmann, H., Automorphismengruppen 8-dimensionaler Ternàrkôrper, Math. Z. 166 (1979), 265–275.Google Scholar
13. Salzmann, H., Kompakte 8-dimensionale projektive Ebenen mit grower Kollineationsgruppe, Math. Z. 176 (1981), 345–357.Google Scholar
14. Salzmann, H., Projectivities and the topology of lines, Geometry — von Staudt's point of view, Proc. Bad Windsheim (1980), 313–337. (Reidel, Dordrecht, 1981).Google Scholar
15. Salzmann, H., Compact 16-dimensional projective planes with large collineation groups, Math. Ann. 261 (1982), 447–454.Google Scholar
16. Salzmann, H., Compact 16-dimensional projective planes with large collineation groups. II, Monatsh. Math. 95 (1983), 311–319.Google Scholar
17. Salzmann, H., Compact 16-dimensional projective planes with large collineation groups. III, Math. Z. 755(1984), 185–190.Google Scholar
18. Salzmann, H., Homogeneous translation groups, Arch. Math. 44 (1985), 95–96.Google Scholar
19. Tits, J., Sur certaines classes d'espaces homogènes de groupes de Lie, Acad. Roy. Belg. Cl. Sci. Mém. Coll. 29 (1955), 1–268.Google Scholar
20. Salzmann, H., Tabellen zu den einfachen Liegruppen und ihren Darstellungen, Lecture Notes in Math. 40 (Springer-Verlag, 1967), 1–53.Google Scholar
21. Varadarajan, V. S., Lie groups, Lie algebras, and their representations (Prentice-Hall, 1974).Google Scholar
22. Vôlklein, H., Transitivitàtsfragen bei linearen Lie-gruppen, Arch. Math. 36 (1981), 23–34.Google Scholar