Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:42:04.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficients in Expansions of Certain Rational Functions

Published online by Cambridge University Press:  20 November 2018

Ronald Evans ,
Mourad E. H. Ismail  and
Dennis Stanton
Ronald Evans
Affiliation:
University of California, San Diego, La Jolla, California
Mourad E. H. Ismail
Affiliation:
Arizona State University, Tempe, Arizona
Dennis Stanton
Affiliation:
University of Minnesota, Minneapolis, Minnesota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The constant term of certain rational functions has attracted much attention recently. For example the Dyson conjecture; that the constant term of

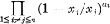
is the multinomial coefficient

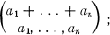
has spawned many generalizations (see [2], [7]). In this paper we consider some other families of rational functions which have interesting constant terms. For example, Corollary 4 states that the constant term of

(1.1)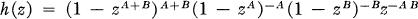

is 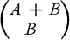. Here, and throughout this paper, A and B denote fixed positive integers.

In order to prove this result, we consider the rational function in two variables

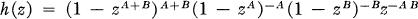
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 1011 - 1024
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Andrews, G. E., Identities in combinatorics II: A q-analog of the Lagrange inversion theorem, Proc. Amer. Math. Soc. 53 (1975), 240–245.Google Scholar
2. Andrews, G. E., Problems and prospects for basic hyper geometric functions, in Theory and applications of special functions (Academic Press, New York, 1975), 191–240.Google Scholar
3. Andrews, G. E., Theory of partitions (Addison-Wesley, Reading, Massachusetts, 1976).Google Scholar
4. Garsia, A., A q-analogue of the Lagrange inversion formula, Houston J. Math. 7 (1981), 205–237.Google Scholar
5. Gessel, I., A noncommutative generalization and q-analoque of the Lagrange inversion formula, Transactions Amer. Math. Soc. 257 (1980), 455–482.Google Scholar
6. Jacobi, C., De resolution aequationum per series infinitas, J. fur die reine und angewandte Math. 6 (1830), 257–286.Google Scholar
7. Macdonald, I., Some conjectures for root systems, SIAM J. Math. Anal., to appear.Google Scholar
8. Mallows, C. L., A formula for expected values, Amer. Math. Monthly 87 (1980), A formula for expected values.Google Scholar
9. Rainville, E. D., Special functions (Macmillan, New York, 1960).Google Scholar
10. Sears, D., On the transformation theory of basic hyper geometric functions, Proc. London Math. Soc. 53 (1951), 158–180.Google Scholar
11. Slater, L. J., Generalized hyper geometric functions (Cambridge University Press, Cambridge, 1966).Google Scholar
12. Titchmarsh, E. C., Theory of functions, second edition (Oxford, 1944).Google Scholar
13. Zeilberger, D., A combinatorial proof of Dyson s conjecture, preprint.Google Scholar