Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:10:56.602Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification Theory and Stationary Logic

Published online by Cambridge University Press:  20 November 2018

Alan H. Mekler
Alan H. Mekler*
Affiliation:
Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Stationary logic L(aa) is obtained for Lωω by adding a quantifier aa which ranges over countable sets and is interpreted to mean “for a closed unbounded set of countable subsets”. The dual quantifier for aa is stat, i.e., stat sφ(s) is equivalent to ¬aa s ¬φ(s). In the study of the L(aa)-model theory of structures a particular well behaved class was isolated, the finitely determinate structures. These are structures in which the quantifier “stat” can be replaced by the quantifier “aa” without changing the validity of sentences. Many structures such as R and all ordinals are finitely determinate. In this paper we will be concerned with finitely determinate first order theories, i.e., those theories all of whose models are finitely determinate.

Example 0.1. [5] The theory of dense linear orderings is not finitely determinate. Let S be a stationary costationary subset of ω1 and

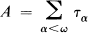
where

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 4 , 01 August 1987 , pp. 893 - 907
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Combase, J., Ph.D. Dissertation, Stanford University, in preparation.Google Scholar
2. Eklof, P. and Mekler, A., Stationary logic of finitely determinate structures, Annals of Math. Logic 17 (1979), 227–270.Google Scholar
3. Harrington, L. and Makkai, M., An exposition of Shelah's ‘Main Gap': counting uncountable models of ω-stable and superstable theories, preprint.Google Scholar
4. Jech, T., Set theory (Academic Press, New York, 1978).Google Scholar
5. Kaufmann, M., Some results in stationary logic, Ph.D. Dissertation, University of Wisconsin (1978).Google Scholar
6. Kueker, D., Back-and-forth arguments and injinitary logics, in Infinitary logic: In Memoriam Carol Karp, Lecture Notes in Math. 527 (Springer-Verlag, Berlin, 1975).Google Scholar
7. Makkai, M., A survey of basic stability theory, with particular emphasis on orthogonality and regular types, preprint.Google Scholar
8. Mekler, A. and Shelah, S., Stationary logic and its friends II, Notre Dame J. of Formal Logic (to appear).CrossRefGoogle Scholar
9. Shelah, S., The number of non-isomorphic models of an unstable first-order theory, Israel J. Math. 9 (1971), 473–487.Google Scholar
10. Shelah, S., Classification of first order theories which have a structure theorem, Bull. Amer. Math. Soc. (to appear).CrossRefGoogle Scholar
11. Shelah, S., The spectrum problem I, -saturated models, the main gap, Israel J. Math. 443 (1982), 324–356.Google Scholar