Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, C. A.
1967.
Intrinsic Functions on Semi-Simple Algebras.
Canadian Journal of Mathematics,
Vol. 19,
Issue. ,
p.
590.
Cullen, C. G.
and
Hall, C. A.
1967.
Functions on Semi-Simple Algebras.
The American Mathematical Monthly,
Vol. 74,
Issue. 1P1,
p.
14.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
Long, J.P.
and
Cullen, C.G.
1974.
Intrinsic functions on real semisimple algebras.
Linear Algebra and its Applications,
Vol. 9,
Issue. ,
p.
199.


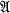 be a finite-dimensional linear associative algebra over the real field
be a finite-dimensional linear associative algebra over the real field 